Method of fault modelling
-
Upload
kutubuddin-ansari -
Category
Education
-
view
71 -
download
0
Transcript of Method of fault modelling

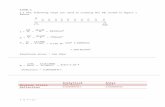
The Geometry of the fault having parameters (length, width, depth, dip angle) can be given by analytically by Green function (G):
2 2
1 1
AL AW
AL AW
G d d
(Okada, 1985 &1992)
Length
Wid
th
DIP
Slip
Length(AL) Wid
th(A
W)
Length
Wid
th
cos sinx ALy d AW
(δ)
Dislocation Theory

(P. Cervelli et. al 2001)
S is Slip For Oblique Slip
S= s.cosα + s.sinα
d= sG(m)
Relationship between dislocation field (d) and the fault geometry G(m)

Since the ruptured area is not a perfect finite rectangular and it contains error the Cervelli equation becomes
Forward Modelling Approach
d= sG(m)+d-sG(m)
0ˆ ˆ ˆd= sG(m)
if
where
m=initial model parameter
ˆ modˆ modˆ mod
s slip
errorS Net slip
d elled dislocaton fields el slipm el parameter
rake of the netslip on the fault plane
For Oblique Slip
S= s.cosα + s.sinα

Coulomb Software
Coulomb software is based on the Boundary Element Method (BEM). The inputs given to Coulomb are estimates of length, width, dip angle, strike slip and dip slip of the modelled fault plane as well as the co-ordinates of the trace of the fault plane.
(Toda et al., 2010)

Coulomb Input File (Toda et al., 2010)

Coulomb Input File (Toda et al., 2010)

The relation between displacement field and the source geometry can be expressed by the following equation:
( )( )
d G md sG m
Where d= displacement vectorm=source geometry (dislocation, length, width, depth, strike, dip)s=slip
(P. Cervelli et al., 2001)
Inverse Modelling

If we have observed data d1, d2, …dn and the Green function of each observation data are G1, G2, …Gn respectively, Then-
1 11 12 1 1
2 21 22 2 2
1 2
.........
.......... . .. . .. . .
.........
m
m
n n n nm m
d G G G md G G G m
d G G G m
11 11 12 1 1
2 21 22 2 2
1 2
.........
.......... . .. . .. . .
.........
m
m
m n n nm n
m G G G dm G G G d
m G G G d
Least square approach

Cartesian Co-ordinate system (x,y,z) the half space occupied region z<0 if fault is located at (0,0,-d) the point force distribution can be given in following form .
Finite Element Method
μ, λ are lames constants

Thrust faults :-F1 and F2 will be horizontal and F3 will be vertical. Normal faults:- F2 and F3 will be horizontal and F1 will be vertical Strike-slip faults:- F1 and F3 will be horizontal and F2 will be vertical


ANSYS (Brick 8 node 185) element, White concentrated area is showing finite rectangular fault

Where Fi is acting force and ui and vi displacements of points and ki
j are Stifness constants

At location of fault points