Boundary Layer Theory_P2

CVEN 311 Fluid Dynamics 1

� Further the equation can be re-written as

MOMENTUM INTEGRAL EQUATION

( ) 0

0 0

h hd dU dU

u u U dy udy h Udx dx dx

ρ − − ρ = ρ − τ

∫ ∫

( ) ( ) 0

0 0

h hd dU

u U u dy U u dydx dx

ρ − + ρ − = τ

∫ ∫

or

( ) ( )2 *

0

d dUU U

dx dxρ θ + ρ δ = τ

� For a flat plate at zero incidence (i.e. no imposed

pressure, dp/dx = 0, then

� Hence,

( ) ( )2 * 0d dUU U

dx dx

τθ + δ =

ρ

MOMENTUM INTEGRAL EQUATIONMOMENTUM INTEGRAL EQUATION of

the boundary layer which forms the

basis for approximate methods of

solving boundary layer problems

0=dx

dUU

0

2

d

U dx

τ θ

ρ=


� In order to use this equation to estimate the boundarylayer thickness as a function of x, we must first:� Obtain a first approximation to the freestream velocity

distribution, U(x). This is determined from inviscid flow theory(the velocity that would exist in the absence of boundarylayer) and depends on body shape.

� Assume a reasonable velocity-profile shape inside theboundary layer

� Derive an expression for τ0 using the result obtained from theprevious item.

� Reviewing the assumptions made in the derivation, it can be seen thatthe equation is:

� Restricted to steady, incompressible, two-dimensional flow with nobody forces parallel to the surface.

� Valid for either a laminar or turbulent boundary layer flow.

� Step 1. Assume a suitable velocity profile for u(y)

inside the BL

� For example, assume a linear velocity

distribution inside a BL

� Determine constants A and B with the boundary

conditions as

� u(0) = 0 → B = 0

� u(δ) = U → A = U/ δ

VON KARMAN’S MOMENTUM INTEGRAL APPROACH

BAyyu +=)(

δ

y

U

u=


� Thus δ

µµτU

y

u

y

=

∂

∂=

=0

0


*

0 0

1 12

u ydy dy

U

δ δδ

δ = − = − = δ

∫ ∫

0 0

1 16

u u y ydy dy

U U

δ δδ

θ = − = − = δ δ

∫ ∫

dx

d

U

θ

ρ

τ=

2

01

6

d

dx U U

δ µ υ= =

ρ δ δ

2( ) 12d

dx U

δ υ=

� Integrating

� Local drag coefficient

� Skin friction drag


2 12 xC

U

υδ = +

At x=0, δ = 0, hence C = 0

2 12 x

U

υδ =

2

2

12 12

Rexx Ux

δ υ= = 12 3.464

Re Rex xx

δ= =

0

2

2 0.5774

Re

2

f

x

cU U

τ µ= = =

ρ ρ δ

3 2 1 2 1 2

0

0

0.5774

L

DF Bdx U L B= τ = ρ υ∫


VON KARMAN’S MOMENTUM INTEGRAL APPROACH� Average drag coeffcient

� Displacement thickness

� Momentum thickness

2

1.1548

2 Re

Df

L

F BLC

U= =

ρ where µ

ρULL =Re

* 1.732

2 Re x

xδδ = =

0.5774

6 Rex

xδθ = =

This problem dealt with linear velocity profile as an approximate solution. The results

obtained are rough. However the exercise illustrates the use of the momentum

integral method. Practice this method with other types of approximated velocity

profile, such as parabolic, sinusoidal, … etc.

� One key point to remember

� Be careful not to confuse the calculation for cf and Cf.

cf is a local calculation at a particular x location

(including x=L) and can only be used to calculate local

shear stress, NOT drag force. Cf is an integrated

average over a specified length (including any x ≤ L)

and can only be used to calculate average shear

stress and the integrated force over the length


EXAMPLE PROBLEM

� Water at 15°C flows over a flat plate at a speed of 1 m/s. Theplate is 0.4 m long and 1 m wide. The boundary layer on eachsurface of the plate is laminar. Assume that the velocity profilemay be approximated as linear. Determine the drag force on theplate.

� Given

� Working fluid is water at T = 15 °C ⇒ ρ = 999 kg/m3 & µ = 1.14 × 10-3

N⋅s/m2

� U = 1 m/s

� L = 0.4 m

� W = 1 m

� The boundary layer on each surface of the plate is laminar

� Velocity profile is linear (assuming approximately)

� Assumptions

� Steady state condition

� Incompressible fluid flow

� Laminar boundary layer

� System diagramU = 1 m/s

L = 0.4 m


� Governing Equations

� Skin friction coefficient definition:

� Reynolds number definition for a flat plate:

2

2

1U

C w

f

ρ

τ=

µ

ρUxx =Re

LAMINAR BOUNDARY LAYER ON A FLAT PLATE:

APPROXIMATE SOLUTION USING PARABOLIC

VELOCITY PROFILE

� Consider two-dimensional laminar boundary

layer flow along a flat plate. Assume the

boundary layer as parabolic.

� Find expressions for:

�The rate of growth of δ as a function of x.

�The displacement thickness, δ*, as a function of x.

�The total friction force on a plate of length L and width b.


� In 1908 Blasius, a student of Prandtl, obtained an exact solution of thefollowing BL equations for a flat plate and demonstrated the shape ofthe boundary layer profile.

� With the following boundary conditions� u(y = 0) = 0

� v(y = 0) = 0

� u→ U as y → ∞

� Blasius’ exact solution is valid only for laminar BL flow with no pressuregradient.

LAMINAR BOUNDARY LAYER (BLASIUS’ EQN.)

Parallel flow along a

plate with zero

pressure gradient

LAMINAR BOUNDARY LAYER � Inside the boundary layer since the viscous forces

are predominant� Reasonable to assume: inertial and viscous forces are of

the same order of magnitude in a laminar boundary layer

Inertial forces/unit volumex

U

x

uu

2

ρρ ≈∂

∂For a flat plate

Viscous forces/unit volume 22

2

δ

µµµ

τ U

y

u

y

u

yy∝

∂

∂=

∂

∂

∂

∂=

∂

∂

If these forces are proportional to each other, then

x

k

Ux

k

x Re2

2 ′=

′=

ρ

µδ2

2

δµ

ρ Uk

x

U′=

x

Uk

υδ= A non-dimensional

parameter

Rex

kk

x Ux

δ µ

ρ= =


RESULTS OF BLASIUS’EXACT SOLUTION

� u approaches to 99 % of U at k = 5.

� In other words when k becomes 5, y becomes 5.

� Therefore using the definition of k, BL thickness atany x becomes

� Using local Reynolds number definition in theabove equation we get

U

xυδ 5=

δ grows with

υ

Uxx =Re

x

x

Re

5=δ

� Shear stress

� Since in the boundary layer

� Replacing δ in the above equation


δµµτ

δ

U

y

uU

y

u

yy

≈

∂

∂=∴≈

∂

∂

== 0

0

0

;

x

U ρµτ

3

0 constant =

xx

fUx

cU Re

0.664

Re

constantconstant

2

2

0 ====

µ

ρρ

τ Blasius’exact analytical solution

cf = local drag coefficient


� Total horizontal force (or skin friction drag)

� Average drag coeffcient

� Displacement thickness



BLUBdxF

L

D

21

0

2123

0 664.0∫ == υρτ

L

Df

U

BLFC

Re

328.1

22==

ρwhere

µ

ρULL =Re

x

x

Re

729.1* =δ

x

x

Re

664.0=θ


Blasius’exact solution

• laminar BL

• over a flat plate

• With zero pressure gradient (dp/dx=0)

Momentum Integral Approach (MIA)

• both laminar and turbulent BLs

• over flat and curved surfaces

• for any known U(x) and poutside (x) distributions


COMPARISON OF DIFFERENT SOLUTIONS

Source: Munson, Yong, Okiishi, “Fundamentals of Fluid

Mechanics”, 3rd ed. Willey, 1998

PROBLEM

� Air flows over a sharp edged flat plate 1 m long,

3 m width with a velocity of 2 m/s. For one side

of the plate, determine δ at the end of the plate,

τ0 at the middle of the plate, FD. [ρ = 1.23 kg/m3;

υ =1.46 × 10-5 m2/s]


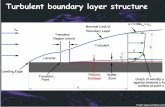
TURBULENT BOUNDARY LAYER

� Turbulent Boundary layers are usually thicker

than laminar ones.

� Velocity distribution in a turbulent boundary

layer is much more uniform than that in a

laminar boundary layer

� Large velocity change occur in a relatively small

vertical distance

� Velocity gradient (dv/dy) is steeper in a turbulent

boundary layer than in laminar boundary layer


� From experiments,

� Velocity distribution in a turbulent boundary profilefollows 1/7th power law i.e.

� Satisfactorily describes velocity distribution for mostof the region of turbulent boundary layer but givesinfinite slope at the wall,

� Therefore it can not be used to predict �0


17u y

U δ

=

( )61

7 7u

1 7 U at y = 0yy

− −∂= δ = ∞

∂

� Instead experimentally obtained measurements of the

shear profile are used such as

� Putting the expression for the 1/7 power law into the

equations for displacement and momentum thickness

14

2

0 0.0225 UU

υ τ = ρ

δ

* 7,

8 72

δδ = θ = δ

δ=99%

δd

δm



� Using momentum thickness obtained and the above �0

relation in the integral momentum equation we can

obtain

� Equating this to the experimental value of shear stress:

2

0

7

72

dU

dx

δτ = ρ

147

0.022572

d

dx U

δ υ =

δ

Integrating gives:

The turbulent boundary grows as x4/5, faster than the laminar

boundary layer where δ increases as x1/2.

2

0

dU

dx

θτ = ρ


51

376.0

−

=

υδ

Uxx ( )5

1

Re

059.0

x

fc =


� To find the total force, integrate over the plate

length


157

0.03672

Uxx

−

θ = δ = υ

2 2

0

0 0

L L

D

dF dx U dx U

dx

θ= τ = ρ = ρ θ∫ ∫

For a plate of length, L, and width B,

15

20.036D

ULF U LB

−

= ρ υ

15C 0.074Re

f L

−= 5 7(5 10 Re 10 )

L× < <


� For , H. Schlichting assumed alogarithmic velocity distribution for the boundary layerflow and obtained a semi-empirical relation as follows

� The previously obtained relations of average dragcoefficient (Cf) including the above, (for laminar as wellas turbulent flows) is applicable for the entire length ofthe plate.

� However, when the plate is of such length as bothlaminar and turbulent boundary layer exist then,

TURBULENT BOUNDARY LAYER7 9(10 Re 10 )

L< <

( )2.58

10

0.455C

log Ref

L

=

15

0.074C

ReRef

LL

A= −

( ) 58.2Relog

370.0

x

fc =61

Re

22.0

xx

=δ

Critical ReCritical ReCritical ReCritical Rexxxx 3333××××101010105555 5555××××101010105555 101010106666 3333××××101010106666

Constant A 1050 1700 3300 8700


15

0.074 1700C

ReRef

LL

= −

Turbulent spots and the transition from laminar to

turbulent boundary layer flow on a flat plate. Flow

from left to right.

(Photograph courtesy of B. Cantwell, Stanford

University.)


PRESSURE GRADIENT INSIDE A BOUNDARY

LAYER

� dp/dx=0: Fluid particles inside the BL slow down due to shear stressonly.� No flow separation can occur.

� dp/dx<0: Pressure decreases in the flow direction (favorable pressuregradient).� Pressure force is in the flow direction. It helps the flow to attach to the

surface even stronger.

� No flow separation can occur.

� dp/dx>0: Pressure increases in the flow direction (adverse pressuregradient).� Pressure force is in opposite direction of the flow.

� Fluid particles close to the wall with low momentum may come to a stop oreven move in opposite direction of the main flow, called backflow.

� Therefore, adverse pressure gradient is the necessary, but notsufficient, condition for separation.

� Boundary layer theory is no longer applicable after the separationpoint.

PRESSURE GRADIENT INSIDE A BOUNDARY

LAYER


FLOW SEPARATION

� Flow separation is generally undesired. It reduces liftforce on an airfoil or increases drag force on a bluntbody.

� Turbulent BLs are more resistive to separationbecause, compared to a laminar one, in a turbulentBL velocities close to the wall are higher.

Separation over an airfoil Separation over a tennis ball

SOLVED IN CLASS

� Air enters a square duct through a 1-ft opening as is shown inFig. Because the boundary layer displacement thicknessincreases in the direction of flow, it is necessary to increase thecross-sectional size of the duct if a constant velocity (U=2 ft/s)is to be maintained outside the boundary layer. Plot a graph ofthe duct size, d, as a function of x for 0 ≤x≤10 ft if U is toremain constant. Assume laminar flow. [ν= 1.57× 10-4 ft2/s]


� Assuming a velocity distribution defined by u/U =

sin (πy/2δ ) determine the general expressions

for growth of the laminar boundary layer and for

the surface shear stress for a smooth flat plate.

PROBLEM 1

� A flat plate is drawn submerged through still

water at a velocity of 9 m s−1. If the plate is 3 m

wide and 20 m long determine the position of

the laminar to turbulent transition and the total

drag force acting on the plate. Take water

temperature as 20 °C. [Ans: 0.01 m, 9.5 kN]


� Estimate the skin friction drag on an airship 92 m

long, average diameter 18 m, being propelled at

130 km h−1 through air at 90 kN m−2 absolute

pressure and 27 °C. [Ans:6.7 kN]

PROBLEM 2

� Air at 20 °C and 760 mm Hg absolute pressure flows past asmooth wind tunnel wall, with a free stream velocity of 160 kmh−1. Determine the position along the wall, in the flowdirection, at which the boundary layer becomes turbulent andthe distance to a boundary layer thickness of 25 mm. All wallmeasurements may be assumed to be taken from the workingsection entrance and edge corner effects may be ignored.

[Ans: 33.6 mm, 1.4 m]

PROBLEM 3


� Show that, if a flat plate, sides a, b in length, is towedthrough a fluid so that the boundary layer is entirelylaminar, the ratio of towing speeds so that the drag forceremains constant regardless of whether a or b is in theflow direction is given by

where Ua is the free stream velocity if side a is in the flowdirection and Ub is the corresponding fluid velocity if b isin the flow direction.

� Repeat Problem above if the boundary layer is consideredfully turbulent.

3 / baUU ba =

9 / baUU ba =

PROBLEM 4

Boundary Layer Theory_P2

Documents

Transcript of Boundary Layer Theory_P2