4. INTEGRAL ANALYSIS OF THE BOUNDARY LAYER...

Turbulent Boundary Layers 4 - 1 David Apsley

h

δ*

boundary-layerprofile

equivalentdisplaced profile

δ*h+h

streamline

boundary

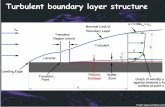
4. INTEGRAL ANALYSIS OF THE BOUNDARY LAYER SPRING 2009 4.1 Characteristic integral lengths 4.2 The momentum-integral relation 4.3 Application to laminar flow 4.4 Application to turbulent flow Examples The integral analysis of boundary layers was originally proposed by Theodore von Kármán and K. Pohlhausen in separate papers in 1921. 4.1 Characteristic Integral Lengths Displacement Thickness

The flow near the surface is retarded, so that the streamlines must be displaced outwards to satisfy continuity. To reduce the total mass flow rate of a frictionless fluid by the same amount, the surface would have to be displaced outward by a distance *, called the displacement thickness:

deficitfluxmassyUUU eeee =⌡

⌠ −=∞

0

d)(*

Momentum Thickness The loss of momentum flux for the mass flux U dy between adjacent streamlines is

yUUU e d)( ×− . Hence the total loss of momentum flux is equivalent to the removal of

momentum through a distance , called the momentum thickness:

tlux deficimomentum fyUUUU eee d)(0

2 =⌡

⌠ −=∞

For incompressible flow (with uniform free-stream density) these take particularly simple forms:

Displacement thickness: ⌡

⌠ −=∞

0

d)1(* yU

U

e

(1)

Momentum thickness: ⌡

⌠ −=∞

0

d)1( yU

U

U

U

ee

(2)

y

U

equalareas

y

U

δ*

ee


Shape Factor The ratio of displacement thickness to momentum thickness is called the shape factor H:

Shape factor: *≡H (3)

Since )1(1eee U

U

U

U

U

U −>− the shape factor is always greater than 1.

A large shape factor is an indicator of a boundary layer near separation.

y

U

ysmall

Hlarge

H

4.2 The Momentum-Integral Relation 4.2.1 Zero-Pressure-Gradient Boundary Layer

0 x

τw

CONTROL VOLUME

streamline

For a zero-pressure-gradient boundary layer (e and Ue constant) the rate of loss of momentum equals the total drag on the surface up to that point; i.e., per unit width:

⌡

⌠==x

wee xxDU0force drag totaldeficitflux momentum

2 d)(321321

Differentiating:

weeUx)(

d

d 2 =

Dividing by 2eeU we can also express it in a simpler non-dimensional form:

2d

d fc

x=

Integrating, gives the total drag coefficient (= average skin-friction coefficient) over length L:

L

LcD

)(2=

The drag coefficient can then be deduced entirely from the downstream velocity profile.


4.2.2 General Case The following derivation applies to a steady, compressible or incompressible, 2-dimensional boundary layer with arbitrary free-stream pressure gradient. For complete generality we will allow for a wall transpiration velocity Vw as well as a wall shear stress w. Start with the integral momentum flux deficit:

⌡

⌠ −=∞

0

2 d)( yUUUU eee

Differentiate with respect to x, taking the differential operator through the integral sign and using the product rule,

{ }

⌡

⌠

∂∂−+−

∂∂=

⌡⌠ −

∂∂=

∞

∞

0

0

2

dd

d)(

)(

d)()(d

d

yx

UU

x

UUUU

x

U

yUUUx

Ux

ee

eee

In the first underlined term substitute from the continuity equation:

y

V

x

U

∂∂−=

∂∂ )()(

In the second underlined term substitute from the boundary-layer momentum equation:

yx

UU

y

UV

x

UU e

ee ∂∂++

∂∂−=

∂∂

d

d

Then

⌡

⌠

∂∂−−−

∂∂+−

∂∂−=

⌡

⌠

∂∂−−

∂∂++−

∂∂−=

∞

∞

0

0

2

dd

d)()(

)(

dd

d

d

d)(

)()(

d

d

yyx

UUU

y

UVUU

y

V

yyx

UU

y

UV

x

UUUU

y

VU

x

eeee

eee

eeee

Collecting y derivatives together, and simplifying using the product rule and the fact that Ue is independent of y,

{ } ⌡

⌠ −−⌡

⌠ +−∂∂−=

∞∞

00

2 d)(d

dd)()(

d

dyUU

x

UyUUV

yU

x eee

eee

⇒ *)(d

d)()(

d

d

0

2ee

eeee U

x

UUUVU

x−

+−−=∞

Since Ue – U and both vanish at y = ∞, whilst U = 0, V = Vw and = w at y = 0,

*)(d

d)(

d

d 2ee

ewewwee U

x

UUVU

x−+=

i.e.

ewwwe

eeee UVx

UUU

x*

d

d)(

d

d 2 +=+


Kármán’s integral relation

43421321

443442143421iontranspirat

wallstresswall

gradient pressure stream-free ofeffect

momentum ofloss of rate

2 *d

d)(

d

dewww

eeeee UV

x

UUU

x+=+ (4)

For constant-density flow the most compact form comes from expanding the first differential

and dividing by 2eU :

e

wfe

e U

Vc

x

U

UH

x+=++

2d

d)2(

d

d (5)

where

2

21

e

wf

Uc = skin-friction coefficient

*=H shape factor

Notes. (1) The results also hold along a curved-wall boundary layer, provided that the radius of curvature is much greater than the thickness of the boundary layer. (2) The integral relations hold whether the boundary layer is laminar, turbulent or transitional. (3) The integral relation is exact only for the correct mean velocity profile. However, the power of the scheme is that it provides an excellent estimate of drag with only a half-decent approximation for U(y). (4) For a flat-plate boundary layer with zero pressure gradient and no wall transpiration, Kármán’s integral relation takes the particularly simple form: Zero pressure-gradient boundary layer:

2d

d fc

x= (6)

In this case the total-drag coefficient LU

LDLc

eD 2

21

)()( = where

⌡

⌠=L

w xLD0

d)( is given by

L

LLcD

)(2)( = (7)

The total drag is entirely determined by the downstream momentum thickness. (5) The shape factor H is only relevant when there is a free-stream pressure gradient (dUe/dx ≠ 0). A large shape factor indicates a boundary layer approaching separation. (6) An alternative proof of Kármán’s integral relation – starting from the differential boundary-layer equations – is given in the Examples Section.


4.3 Application to Laminar Flow A fully-developed profile may be approximated by:

>

≤= ),(

yU

yy

fUU

e

e (8)

where 0)1(,1)1(,or0)0(,0)0( =′=∞≠′= ffff . (Why is the second condition important?) The integral boundary-layer depths are proportional to :

,* BA == (9) and the skin-friction coefficient

�221

0

Re

)0(2d

d

C

U

f

U

y

U

cee

yf =

′== = (10)

where A, B and C are constants determined by the particular profile adopted:

)0(2,d)1(,d)1(1

0

1

0

fCffBfA ′=⌡

⌠ −=⌡

⌠ −= (11)

Substituting the expressions for and cf into the integral relation:

=⇒=⇒=

ee

f

UB

C

xU

C

xB

c

x d

d

2d

d

2d

d 2

Hence:

2/12/1

=eU

x

B

C or 2/1

2/1

Re−

= xB

C

x (12)

(x is measured from some virtual origin; in practice, this can be taken as the leading edge).

Since 2/1x∝ we have xx 2

1

d

d = and hence

xx

c f d

d2 ==

Summary of Results For a Zero-Pressure-Gradient Laminar Boundary Layer

B

AHBA === ,,*

)(2)(, LcLcx

c fDf ==

where

)0(2,d)1(,d)1(1

0

1

0

fCffBfA ′=⌡

⌠ −=⌡

⌠ −=

eU

x

B

C2/1

=


Thus, assuming only that the profile is self-similar, but without any knowledge about its precise form, we can confirm that

2/1x∝ (or 2/1Re−∝ xx) and 2/1Re)( −∝ LD Lc

The simplest profile satisfying

on 0d

d,

0on 0

===

==

yy

UUU

yU

e

is (the channel-flow profile)

)2(yy

UU e −= or 22)( −=f

This has 4,, 15

231 === CBA and gives the following approximations.

Approximation Blasius solution

*

eU

x83.1

eU

x72.1

eU

x730.0

eU

x664.0

H 2.5 2.59

In both cases,

x

c f =

)(2)( LcLc fD =

Thus, the drag is correct to within 10% and the shape factor to within 3.5%, even for a simple approximation. Much better approximations are given in the Examples section.


4.4 Application to Turbulent Flow The momentum integral relation for a zero-pressure-gradient boundary layer is

2d

d fc

x=

To make this tractable we adopt the power-law approximations that we have met before:

Velocity profile: 7/1)(y

U

U

e

= (13)

Skin-friction coefficient: 6/1�Re0205.0 −=fc (where Re� eU= ) (14)

From the first of these we can compute displacement and momentum thickness:

/,7/1 yU

U

e

==

Displacement thickness:

8

1d)1(d)1(*

1

0

7/1

�0

=⌡

⌠ −=⌡

⌠ −≡ yU

U

e

(15)

Momentum thickness:

72

7d)1(d)1(

1

0

7/17/1

�0

=⌡

⌠ −=⌡

⌠ −≡ yU

U

U

U

ee

(16)

Shape factor:

7

9* =≡H (17)

Substituting for skin-friction coefficient cf and momentum thickness in the momentum integral relation,

6/1)(01025.0d

d

72

7

eUx=

⇒ xU e

d)(01025.0d72

7 6/16/1 =

⇒ xU e

6/16/7 )(01025.07

6

72

7 =×

⇒ 6/16/7 )(123.0)(xUx e

=

Hence

7/1Re166.0 −= xx or 7/6� Re166.0Re x= (18)

Thus, the boundary layer grows as

7/6x∝

Since 7/6x∝ we have xxx 12

1

7

6

d

d == , and hence:


7/1Re0277.012

12

d

d2 −=×== xf xx

c (19)

(Alternatively, use 6/1�Re0205.0 −=fc and substitute for Re�.) 7/1Re032.0)(

6

72)( −=== LfD Lc

LLc (20)

i.e. the total drag coefficient is only 7/6 times the local skin friction coefficient at the end of the plate. Summary of Results for a Zero-Pressure-Gradient Turbulent Boundary Layer Boundary-layer depth:

7

9,

72

7,

8

1* === H

where

7/1Re166.0 −= xx or 7/6x∝

Frictional drag: 7/1Re0277.0 −= xfc

7/1Re032.0)(6

7)( −== LfD LcLc

Note. An earlier and alternative correlation by Prandtl (see Q3 in the Examples) and based on pipe-flow data gave a skin friction coefficient proportional to 5/1−x and resulted in a drag coefficient 5/1Re072.0)( −= LD Lc . This is still widely used today.

0

0.001

0.002

0.003

0.004

0.005

0.006

1.00E+05 1.00E+06 1.00E+07 1.00E+08

ReL

c D

Prandtl

Modern


Examples Question 1. Show that, for a power-law velocity profile of the form

)(/1

<

= yy

U

Un

e

the displacement thickness, momentum thickness and shape factor are given by

1

1*

+=

n,

)2)(1( ++=

nn

n,

n

nH

2+=

Question 2. Laminar boundary layer profiles may be assumed to be approximately of the form

),(y

fUU e ==

where 0)1(,1)1(,0)0( =′== fff . Use an integral analysis with the following profiles to find expressions for *, , H, cf and cD and compare with Blasius’ solution.

(a) 321

23 −

(b) 4322 +−

(c) )2

sin(

Question 3. (White) An alternative (but less accurate) analysis of turbulent flat-plate flow was given by Prandtl in 1927, using a wall shear-stress formula from pipe flow:

4/1

20225.0

=

eew U

U

Show that an integral analysis with this formula and a 1/7 power law profile for velocity leads to the following relations for turbulent flat-plate flow:

5/1Re

37.0

xx= ,

5/1Re

058.0

xfc = ,

5/1Re

072.0)(

LD Lc =

Question 4. Show that, in general, if the skin-friction coefficient and momentum thickness for a zero-pressure-gradient flat-plate boundary layer are related by

nf Ac /1�Re−=

then

1

11

Re2

)1

( +−+

+= nx

n

n

A

n

n

x,

xn

nc f 1

2

+= , )()

1()( Lc

n

nLc fD

+=

Use this to confirm the results in Section 4.4 and Question 3 above.


Question 5. Why would a simple power law be a bad approximation to a laminar boundary-layer velocity profile? Question 6. For purely laminar or purely turbulent flat-plate boundary layers the momentum thickness θ at distance x from the leading edge is given by:

=θ−

−

)turbulent(,Re0158.0

)laminar(,Re664.07/1

2/1

x

x

x

where /Re xU ex = and Ue = free-stream velocity, = kinematic viscosity.

In practice, a turbulent boundary layer is preceded by an initial laminar region. Since fcx 2

1/dd = and the

skin-friction coefficient cf is finite, the momentum thickness must be continuous at the transition point. Irrespective of any intermediate development, the total drag coefficient for one side of a plate of length L depends only upon the momentum thickness at the end:

L

LLcD

)(2)(

θ=

(a) Develop a procedure, illustrated by a flowchart showing calculation steps, or by a computer program, to find the momentum thickness at the end of, and total drag coefficient for, a flat plate of arbitrary length L. (Rex,tr is assumed to be given.)

Using this procedure, find: (b) the transition length; (c) the momentum thickness at the downstream end; (d) the drag coefficient cD; (e) the total drag on one side of a smooth rectangular plate of size 4 m × 2 m in an air

flow of 8 m s–1 parallel to the long side. Take Rex,tr = 5×105 and, for air, = 1.2 kg m–3, = 1.5×10–5 m2 s–1. Question 7. A wind tunnel has a test section 0.5 m square and 6 m long. To preserve a constant free-stream velocity it is sometimes desirable to slant the walls outward. (a) Explain the purpose of this wall adjustment. (b) If only the roof is to be adjusted, estimate the angle at which it should be slanted in

order to preserve a free-stream velocity of 40 m s–1 over a working section from x = 2 m to x = 4 m, stating any assumptions made.

Question 8. A square-section duct of side 30 cm and length 12 m carries a throughflow of air at flow rate 3 m3 s–1. Assuming that turbulent boundary layers grow along the side walls from the front edge, estimate: (a) the pressure drop along the duct; (b) the drag on the side walls.

laminar

turbulent

transition pointx

Ue


Question 9. Starting from the boundary-layer equations in differential form:

yx

UU

y

UV

x

UU e

ee ∂∂+=

∂∂+

∂∂

d

d (momentum)

0)()( =

∂∂+

∂∂

y

V

x

U (continuity)

derive Kármán’s integral relation. Question 10. A boundary-layer mean-velocity profile is approximated by

>

<=)(

)(ln��

yU

yyu

Eu

U

e

where U is continuous at y = . Find * and in terms of u�/Ue and . Question 11. Assume that the following mean-velocity profile holds across a turbulent boundary layer.

)(2

)ln(1 �� y

fByu

u

U ++= where 32 23)( η−η=ηf

(a) Find an expression for U/Ue as a function of and the quantity , where

eU

u�= , )(δ≡ UU e

(b) Hence, or otherwise, show that the displacement thickness δ* is given by:

)1(* +=

(c) Find a similar expression for / where is the momentum thickness. Question 12. In a 2-dimensional, incompressible boundary layer the energy thickness E may be defined by the integral energy flux deficit:

⌡

⌠ −=∞

0

223 d)( yUUUU eEe

where Ue is the free-stream velocity and U is the wall-parallel mean-velocity component in the boundary layer. Using the boundary-layer equations with shear stress , derive the following relation for incompressible boundary-layer flow over a plane surface with wall transpiration velocity Vw:

2

0

3 d2)(d

dewEe UVy

y

UU

x+

⌡

⌠∂∂=

∞

Give an interpretation of all the terms.


Answers (2)

Profile x

U e* x

U e H

(a) 321

23 − 74.1

13

70

4

32/1

=

646.070

117

2

12/1

=

69.213

35 =

(b) 4322 +− 75.137

35

5

92/1

=

685.035

37

3

22/1

=

55.274

189 =

(c) )2

sin( 74.1)2/2(

22/1

=−

− 655.0)2/2( 2/1 =− 66.2

2/2

2 =−−

(d) Blasius 1.72 0.664 2.59

In all cases,

x

c f = , )(2)( LcLc fD =

(6) (b) xtr = 0.94 m (c) L = 6.8×10–3 m (d) cD = 0.0034 (e) D = 1.05 N (7) (b) 0.41 degrees (8) (a) 560 Pa (b) 56 N

(10) *�

eU

u=

)21(��

ee U

u

U

u−=

(11) (a) { })123(2ln1 32 −−++=eU

U

(c)

++−+= 22

35

52

6

192)1(

4. INTEGRAL ANALYSIS OF THE BOUNDARY LAYER...

Documents

Transcript of 4. INTEGRAL ANALYSIS OF THE BOUNDARY LAYER...