Problem solutions, 26 October 20111

D. E. Soper2

University of Oregon28 October 2011

Sakurai, 2.1 We use

d

dtSi(t) = −i[Si(t), H] . (1)

With H = ωSz we have,

d

dtSx = − iω[Sx, Sz] = −ωSy ,

d

dtSy = − iω[Sy, Sz] = ωSx ,

d

dtSz = − iω[Sz, Sz] = 0 .

(2)

The solution of this is

Sx(t) = Sx(0) cos(ωt)− Sy(0) sin(ωt) ,

Sy(t) = Sx(0) sin(ωt) + Sy(0) cos(ωt) ,

Sz(t) = Sz(0) .

(3)

To verify this, just differentiate.

Sakurai, 2.3 The hamiltonian is H = ωSz with ω = |e|B/me. The particle

starts in the state∣∣~S · ~n,+⟩. After time t it is in state

e−iωtSz∣∣~S · ~n,+⟩ . (4)

The probability that, if we measure at time t, it will be found to be in the∣∣Sx,+⟩

state is

P (t,+) =∣∣∣⟨Sx,+

∣∣e−iωtSz∣∣~S · ~n,+⟩∣∣∣2 . (5)

1Copyright, 2011, D. E. Soper2soper@uoregon.edu

1

To evaluate the matrix element, it is convenient to use the∣∣Sz,±

⟩basis:⟨

Sx,+∣∣e−iωtSz

∣∣~S · ~n,+⟩ =∑j=±

⟨Sx,+

∣∣Sz, j⟩e∓iωt/2

⟨Sz, j

∣∣~S · ~n,+⟩ . (6)

Now we recall that ⟨Sx,+

∣∣Sz,+⟩

= 1/√

2 ,⟨Sx,+

∣∣Sz,−⟩

= 1/√

2 .(7)

We also recall from a previous problem that⟨Sz,+

∣∣~S · ~n,+⟩ = cos(β/2) ,⟨Sz,−

∣∣~S · ~n,+⟩ = sin(β/2) .(8)

Thus⟨Sx,+

∣∣e−iωtSz∣∣~S · ~n,+⟩ =

1√2e−iωt/2 cos(β/2) +

1√2e+iωt/2 sin(β/2) . (9)

Taking the absolute square of this gives

P (t,+) =1

2

[cos2(β/2) + sin2(β/2) + 2 cos(β/2) sin(β/2) cos(ωt)

]=

1

2+ cos(β/2) sin(β/2) cos(ωt)

=1

2+

1

2sin(β) cos(ωt) .

(10)

Note that the probability that the system would be found to be in the∣∣Sx,−⟩

is P (t,−) = 1− P (t,+). That is

P (t,−) =1

2− 1

2sin(β) cos(ωt) . (11)

Then the expectation value of Sx at time t is⟨Sx(t)

⟩=

1

2P (t,+)− 1

2P (t,−)

=1

2sin(β) cos(ωt) .

(12)

2

Is this sensible? If we set β = 0 or β = π then the spin is starting in the±z direction and the only thing that happens is that the wave function gets aphase that changes as time increases. The probability to find the spin alongthe +x direction should be zero, and the calculation indeed gives zero. If weset β = π/2, then the spin starts in the +x direction. Then the spin stateshould change. Classically, the spin vector rotates around the z axis withangular frequency ω. Our result is consistent with this classical expectation.

Special problem. A free particle starts at t = 0 with x-space wave function

ψ(x.0) =1

(2π)1/41√aeik0x exp

(− x2

4a2

). (13)

Then its p-space wave function is (from our class notes)

ψ̃(p, 0) =1

(2π)1/4

√2a exp

(−a2(p− k0)2

). (14)

We want to find the x-space wave function at later times. To do that, wenote that the p-space wave function at later times, using H = p2/(2m), is

ψ̃(p, t) =

√2a

(2π)1/4exp

(−i p

2

2mt

)exp

(−a2(p− k0)2

). (15)

We have, in general,

ψ(x, t) =

∫dp

1

(2π)1/2exp(ipx) ψ̃(p, t) . (16)

Thus

ψ(x, t) =

√2a

(2π)3/4

∫dp exp(ipx) exp

(−i p

2

2mt

)exp

(−a2(p− k0)2

). (17)

We can perform the integration by completing the square in the exponent.The exponent is

A ≡ −(a2 + i

t

2m

)p2 + 2(a2k0 + ix/2)p− a2k20 . (18)

3

We write this as

A = −(a2 + i

t

2m

)p̃2

+ (a2k0 + ix/2)2(a2 + i

t

2m

)−1− a2k20 .

(19)

where

p̃ = p− (a2k0 + ix/2)

(a2 + i

t

2m

)−1. (20)

We can further rewrite this as

A = − (p′)2 + (a2k0 + ix/2)2(a2 + i

t

2m

)−1− a2k20 . (21)

where

p′ =

(a2 + i

t

2m

)1/2

p̃ (22)

We can simplify the p′ independent part of this. The first thing that weshould do is to avoid having a complex denominator. To do that, we writeA as

A = − (p′)2 +

(a4 +

t2

4m2

)−1 (a2k0 + i

x

2

)2(a2 − i t

2m

)− a2k20 . (23)

Then we can put the p′ independent terms over a common denominator,

A = − (p′)2 −(a4 +

t2

4m2

)−1B . (24)

where

B = −(a2k0 + i

x

2

)2(a2 − i t

2m

)+ a2k20

(a4 +

t2

4m2

). (25)

Now we can calculate B:

B = −(a4k20 −

x2

4+ ia2k0x

)(a2 − i t

2m

)+ a6k20 +

a2k20t2

4m2

=a2

4

[x2 − 2k0xt

m+k20t

2

m2

]− i[a4k0x−

(a4k20 −

x2

4

)t

2m

].

(26)

4

Thus

B =a2

4

[x− k0t

m

]2− i[a4k0x−

(a4k20 −

x2

4

)t

2m

]. (27)

Now that we have the exponent, we can perform the integration. First,∫ ∞−∞

dp · · · =∫ ∞−∞

dp̃ · · · . (28)

Then ∫ ∞−∞

dp̃ · · · =(a2 + i

t

2m

)−1/2 ∫ ∞−∞

dp′ · · · . (29)

(In each of these steps, the integration contour moves, but there are no polesof the integrand and the integral is convergent at large p̃ and p′, so we it isallowed to move the integration contour.) Finally,∫ ∞

−∞dp′e−p

′2=√π . (30)

Putting this together, we have

ψ(x, t) =

√a

(2π)1/4

(a2 + i

t

2m

)−1/2exp

(−(a4 +

t2

4m2

)−1B

), (31)

where B is given in Eq. (27).This has rather complicated oscillations, corresponding to the imaginary

part of B. The probability density is pretty simple:

|ψ(x, t)|2 =a

(2π)1/2

(a4 +

t2

4m2

)−1/2exp

(− a2 [x− k0t/m]2

2(a4 + t2/(4m2))

), (32)

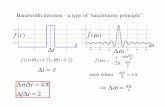
The probability is centered at x = k0t/m. That is, the center of the wavepacket moves with a constant velocity v0 = k0/m. The width starts out ata2, but it grows with t. That is, the wave packet spreads out with time.

5