On the K13 problem in the Oseen-Frank theory of nematic ...Nematic liquid crystals modelling 1...

On the K13 problem in the Oseen-Frank theory ofnematic liquid crystals

Arghir Dani Zarnescu

University of Sussexand

“Simion Stoilow” Institute of the Romanian Academy

joint work with

Stuart Day (U of Sussex)

24 October 2015

Conference in Honour of Jerry Ericksen’s90th Birthday

Nematic liquid crystals modelling

1

Continuum level modelling through functions n : Ω ⊂ R3 → S2

Many deficiencies, particularly related to discontinuities and defect patterns,but still the most widely-accepted theory.

Good experimental relevance.

1Simulation by C. Zannoni group

Energy functionals

Equilibrium configurations obtained as minimizers of the energy functional:

F [n] =

∫Ω

g(n,∇n) dx

with g satisfying the physical requirements:

Frame indiference: g(Qn(P),Q∇n(P)Q t ) = g(n(P),∇n(P)), for allQ ∈ SO(3) and at any point P ∈ Ω

Material symmetry: g(−n,−∇n) = g(n,∇n)

One also needs the energy to be bounded from below in order to have aminimizer...Energy density g:

Oseen (1933), Frank (1958)-phenomenological derivation

Nehring & Saupe (1971)-molecular expansion derivation

Energy functionals


F [n] =

∫Ω

g(n,∇n) dx




One also needs the energy to be bounded from below in order to have aminimizer...

Energy density g:



Energy functionals


F [n] =

∫Ω

g(n,∇n) dx




One also needs the energy to be bounded from below in order to have aminimizer...Energy density g:



The molecular expansions: the Kαβ,Iαβ terms (I)

The average energy between the two volume elements at points P and P′ is givenby f dτ dτ′, where, in cylindrical coordinates f depends on the four quantitiesdefining the position and direction of two vectors relative to each others, namely(r ′, x′3,∆nr ,∆nα).

Switching back to cartesian coordinates a Taylor expansion gives:

f = f0 +3∑

p=1

∑ν=r ,α

i=1,2

fνaνini,px′p +12

3∑p,q=1

∑ν=r ,α

i=1,2

fµνaνiaµjni,pnj,q +∑ν=r ,α

i=1,2

fνaνini,pq

x′px′q + . . .

Note that linear terms of the second derivatives of n make contributions of sameorder as quadratic terms of first derivatives.The energy density at P is obtained by integrating on a sphere around P:

g(P) =3∑

p=1

2∑i=1

cipni,p +3∑

p,q=1

(2∑

i,j=1

cijpqni,pnj,q +2∑

i=1

cipqni,pq) + . . .


The average energy between the two volume elements at points P and P′ is givenby f dτ dτ′, where, in cylindrical coordinates f depends on the four quantitiesdefining the position and direction of two vectors relative to each others, namely(r ′, x′3,∆nr ,∆nα).Switching back to cartesian coordinates a Taylor expansion gives:

f = f0 +3∑

p=1

∑ν=r ,α

i=1,2


3∑p,q=1

∑ν=r ,α

i=1,2


i=1,2

fνaνini,pq

x′px′q + . . .


g(P) =3∑

p=1

2∑i=1

cipni,p +3∑

p,q=1

(2∑

i,j=1

cijpqni,pnj,q +2∑

i=1

cipqni,pq) + . . .



f = f0 +3∑

p=1

∑ν=r ,α

i=1,2


3∑p,q=1

∑ν=r ,α

i=1,2


i=1,2

fνaνini,pq

x′px′q + . . .

Note that linear terms of the second derivatives of n make contributions of sameorder as quadratic terms of first derivatives.

The energy density at P is obtained by integrating on a sphere around P:

g(P) =3∑

p=1

2∑i=1

cipni,p +3∑

p,q=1

(2∑

i,j=1

cijpqni,pnj,q +2∑

i=1

cipqni,pq) + . . .



f = f0 +3∑

p=1

∑ν=r ,α

i=1,2


3∑p,q=1

∑ν=r ,α

i=1,2


i=1,2

fνaνini,pq

x′px′q + . . .


g(P) =3∑

p=1

2∑i=1

cipni,p +3∑

p,q=1

(2∑

i,j=1

cijpqni,pnj,q +2∑

i=1

cipqni,pq) + . . .

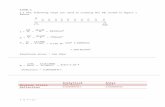
The molecular expansions: the Kαβ,Iαβ terms (II)

Coefficients and their symmetry:

c11 = c22= K1 c12 = −c21 = K2

c1111 = c2222= 12 K11 c1122 = c2211= 1

2 K22 c1133 = c2233= 12 K33

c1212 = c11221= 12 K24 = 1

4 (K11 − K22) c113 = c223= 12 K13 c123 = −c213 = 1

2 K23

Then the energy density is:

g =K1 div n − K2(n · curl n) +12

K11 (div n)2︸︷︷︸:=I11

+12

K22 (n · curl n)2︸︷︷︸:=I22

+12

K ′33 (n · ∇n)2︸︷︷︸:=I33

− K12(n · curl n)(div n) −(K22 + K24)

2((div n)2 − tr(∇n)2)︸︷︷︸

:=I24

+K13 n · ∇div n︸︷︷︸:=I13

− K23n · ∇(n · curl n)

A bit of history

Oseen(1933) introduced the K13 term phenomenologically

Frank (1958) ignored the K13 term in his phenomenological theory

Nehring and Saupe (1971) reintroduced the K13 term on a molecular basis

Oldano and Barbero (1985) found an example involving the K13 term and

making the energy unbounded from below!

Null Lagrangians and Nilpotent energies: Ericksen’s work

In 1962 J.L. Ericksen showed that an energy density that depends just on n or ∇n(on Ω!) does not contribute to the Euler-Lagrange equations (is a “nilpotentenergy”) if and only if it can be expressed in the form:

A +∂Bi

∂njnj,i + 2

∂Bpqi

∂njni,pnj,q + Bdet(∇n)

with A a constant and Bs functions of n only, such that Bpqi = −Bqpi .

Furthermore, assuming the physical invariances under orthogonal transformationshe reduced it to:

H [(nk ,k ni,i − ni,k nk ,i] + 2H′ [ni,jnp,qnpnq − nq,pnj,qnjnp]

But no second order derivatives....

The “tame null-Lagrangian” I24

K24(tr(∇n)2 − (div n)2) = K24div ((∇n)n − (div n)n)

Let∇sn = ∇n(Id − ν ⊗ ν)

be the surface gradient of n and

divsn = tr(∇sn).

These depend only on the boundary values of n!!!Then one can check that

((∇n)n − (div n)n) · ν = ((∇sn)n − (divs n)n) · ν

For K13 , 0 the energy is unbounded from below(Oldano and Barbero ’85):

Take parallel plates at height 0 and d and consider configurations dependingjust on one variable, say z:

n(z) = (cos(θ(z)), sin(θ(z))) , z ∈ [0, d]

where θ is the angle between n and the z axis (with z axis parallel on theplates).

Consider equal elastic constants, K24 = 0 but K13 , 0. Then the energyreduces to: ∫ d

0

K2

(dθdz

)2

+ K13 [sin(2θ(0))θ′(0) − sin(2θ(d))θ′(d)]

so we can get arbitrarily negative energy...

..as long as θ(0), θ(d) < 0, π2 .

But for some special boundary conditions, hometropic and tangential(θ(0), θ(d) ∈ 0, π2 ) things are OK in this example.

A formal reduction: the K24, I13

K24I24 + K13I13 = K24[tr(∇n)2 − (div n)2] + K13div [(div n)n]

= K24[tr(∇n)2 − (div n)2] ∓ K13[tr(∇n)2 − (div n)2]

+ K13

[(div n)2 + (n · ∇)(div n)

]

= (K24 − K13)︸︷︷︸def=K24

[tr(∇n)2 − (div n)2]︸︷︷︸I24

+K13[tr(∇n)2 + (n · ∇)(div n)]

= K24I24 + K13(ni,jnj,i + ninj,ji)

= K24I24 + K13(ninj,i),j

= K24I24 + K13 div [(n · ∇)n]︸︷︷︸def=I13

= K24I24 + K13I13

A formal reduction: the K24, I13

K24I24 + K13I13 = K24[tr(∇n)2 − (div n)2] + K13div [(div n)n]

= K24[tr(∇n)2 − (div n)2] ∓ K13[tr(∇n)2 − (div n)2]

+ K13

[(div n)2 + (n · ∇)(div n)

]= (K24 − K13)︸︷︷︸

def=K24

[tr(∇n)2 − (div n)2]︸︷︷︸I24

+K13[tr(∇n)2 + (n · ∇)(div n)]

= K24I24 + K13(ni,jnj,i + ninj,ji)

= K24I24 + K13(ninj,i),j

= K24I24 + K13 div [(n · ∇)n]︸︷︷︸def=I13

= K24I24 + K13I13

Natural Question: given that the energyis unbounded from below

is there anything to do so to salvage the theory...?

Natural answer: how about local minimizers?

Second Natural Question: Local minimizers in what sense?

Functional spaces and critical points

Question: What is the natural function space in which to study the Oseen-Frankfunctional?

F [n] =

∫Ω

K2|∇n|2 + K24(tr(∇n)2 − (div n)2) + K13[(div n)2 + (n · ∇)div n] dx

The function spaces should be chosen so that the energy makes sense forfunctions in it... One possible choice:

A = W1,2(Ω;S2) ∩W2,1(Ω;S2)

Natural question revisited: Is this a good space in which to look for localminimizers/critical points?



F [n] =

∫Ω


The function spaces should be chosen so that the energy makes sense forfunctions in it...

One possible choice:

A = W1,2(Ω;S2) ∩W2,1(Ω;S2)




F [n] =

∫Ω


The function spaces should be chosen so that the energy makes sense forfunctions in it... One possible choice:

A = W1,2(Ω;S2) ∩W2,1(Ω;S2)


Critical points and the relevance of the W2,1(Ω;S2) space

Take ϕ ∈ Cc1(Ω;R3). Then we have:

ddt|t=0E[

n + tϕ|n + tϕ|

] =K2

∫Ω∇n : ∇ϕ − |∇n|2n · ϕ dx + K24 . . .︸︷︷︸

=0

+K13 . . .︸︷︷︸=0

= 0

with the K24 term and the K13 terms being zero because both n+tϕ|n+tϕ| and ∇( n+tϕ

|n+tϕ| )do not change on the boundary as t varies!

Using that n has a bit more regularity than the standard harmonic maps, namelyn ∈ W2,1 we can integrate by parts, to get:

K2

∫Ω

(∆n + n|∇n|2) · ϕ dx = 0

and thus, since ϕ was arbitrary:

∆n + n|∇n|2 = 0, a.e. in Ω.

The boundary reductionWe take now test functions ϕ ∈ C1(Ω;R3) with ϕ(x) = 0,∀x ∈ ∂Ω (thus this timethe gradient of ϕ might be non-zero on the boundary). We have:

ddt|t=0E[

n + tϕ|n + tϕ|

] =K2

∫Ω∇n : ∇ϕ − |∇n|2n · ϕ dx︸︷︷︸

=0

+K24 . . .︸︷︷︸=0

+ K13

∫∂Ω

3∑β,α=1

ϕβ,αnα (νβ − nβ〈n, ν〉) dS = 0

and the K and K24 terms are zero.

We are left with ∫∂Ω

∂ϕβ

∂ν〈n, ν〉 (νβ − nβ〈n, ν〉) dS = 0

for β = 1, 2, 3.Choosing ϕ suitably we get:

〈n, ν〉 ∈ 0,±1


ddt|t=0E[

n + tϕ|n + tϕ|

] =K2

∫Ω∇n : ∇ϕ − |∇n|2n · ϕ dx︸︷︷︸

=0

+K24 . . .︸︷︷︸=0

+ K13

∫∂Ω

3∑β,α=1


and the K and K24 terms are zero.We are left with ∫

∂Ω

∂ϕβ

∂ν〈n, ν〉 (νβ − nβ〈n, ν〉) dS = 0

for β = 1, 2, 3.

Choosing ϕ suitably we get:

〈n, ν〉 ∈ 0,±1


ddt|t=0E[

n + tϕ|n + tϕ|

] =K2

∫Ω∇n : ∇ϕ − |∇n|2n · ϕ dx︸︷︷︸

=0

+K24 . . .︸︷︷︸=0

+ K13

∫∂Ω

3∑β,α=1


and the K and K24 terms are zero.We are left with ∫

∂Ω

∂ϕβ

∂ν〈n, ν〉 (νβ − nβ〈n, ν〉) dS = 0

for β = 1, 2, 3.Choosing ϕ suitably we get:

〈n, ν〉 ∈ 0,±1

Homeotropic boundary conditions and null Lagrangians

We take n = ν on ∂Ω. Then we have:

∫ΩI13 =

∫Ω

[ninj,i],j dx

=

∫∂Ω

ninj,iνj dσ =

∫∂Ω

ninj,inj dσ

=

∫∂Ω

12

ni(njnj),i dσ = 0

In terms of the original variables , we have:∫Ω

K24I24 + K13I13 dx =

∫Ω

(K24 − K13) [tr(∇n)2 − (div n)2]︸︷︷︸I24

Tangential boundary conditions and null Lagrangians

We take n · ν = 0 on ∂Ω. Then we have directly in terms of the original variables:∫Ω

K24I24 + K13I13 dx =

∫∂Ω

K24 ((∇n)n) · ν − K24(div n) n · ν︸︷︷︸=0

+K13(∇ · n) n · ν︸︷︷︸=0

dσ

= K24

∫∂Ω

ni,jnjνi dσ

= −K24

∫∂Ωνi,jninj dσ

Tangential boundary conditions, I24 and the secondfundamental formSome differential geometry:

for a smooth surface, S = ∂Ω the normal ν : S → S2 is the Gauss map.

dνP : TPS → Tν(P)S2 ∼ TPS

The second fundamental form Πp is related to dνP through:

IIp(n, n) = −dνP(n) · n

and for |n| = 1 this gives the curvature of the normal section.The last expression is νi,jninj , i.e. the I24 term for tangential boundaryconditions

2

2Diagram from Wikipedia-on curvature

The homeotropic versus normal boundary conditions,distinguishing K13 and K24

Thus we have:

For homeotropic boundary conditions the K13 contribution is the same as theK24 contribution but with a negative sign.

For tangential boundary conditions the K13 contribution vanishes and the leftK24 contribution has a geometrical meaning.

Thus one needs a suitable combination of the two types of boundary conditions todetect a non-trivial K13 contribution!

Conclusions

A natural question:• Are there local minimizers for the Oseen-Frank energy with the K13 , 0?

The answer depends on the functional space....A “natural” choice, W1,2(Ω;S2) ∩W2,1(Ω;S2):

I forces the critical points to have homeotropic or tangential boundary conditions.I For these boundary conditions the K13 term either vanishes (tangential) or

becomes part of K24 (homeotropic).

Possible relevance to nematic droplets...

• Open question: could a different functional spaces provide a different answer?

Note though that it is a matter also of geometry not only of the functional space,i.e. some geometries and associated boundary conditions might be incompatiblewith the existence of local minimizers.

THANK YOU!

and

Happy 90th Birthday to Jerry!

On the K13 problem in the Oseen-Frank theory of nematic ...Nematic liquid crystals modelling 1...

Documents

Transcript of On the K13 problem in the Oseen-Frank theory of nematic ...Nematic liquid crystals modelling 1...