JU –

2017

/HL

1

Dynamics and control of mechanical systemsDate ContentDay 1(01/08)

• Review of the basics of mechanics. • Kinematics of rigid bodies - coordinate transformation, angular velocity

vector, description of velocity and acceleration in relatively moving frames. Day 2(03/08)

§ Euler angles, Review of methods of momentum and angular momentum of system of particles, inertia tensor of rigid body.

• Dynamics of rigid bodies - Euler's equation, application to motion of symmetric tops and gyroscopes and problems of system of bodies.

Day 3(05/08)

• Kinetic energy of a rigid body, virtual displacement and classification of constraints.

• D’ Alembert’s principle. Day 4(07/08)

• Introduction to generalized coordinates, derivation of Lagrange's equation from D’ Alembert’s principle.

• Small oscillations, matrix formulation, Eigen value problem and numerical solutions.

Day 5(09/08)

• Modelling mechanical systems, Introduction to MATLAB®, computer generation and solution of equations of motion.

• Introduction to complex analytic functions, Laplace and Fourier transform.Day 6(11/08)

• PID controllers, Phase lag and Phase lead compensation. • Analysis of Control systems in state space, pole placement, computer

simulation through MATLAB.

DMS6021 - Dynamics and Control of Mechanical Systems

JU –

2017

/HL

2

Fundamental principlesPurpose: Kinetic energy

Focus on4 Kinetic energy of rigid bodies4 Concept of virtual work and virtual dispalcement4 Classification of constraints4 D'Alembert's Principle4 Examples

DMS6021 - Dynamics and Control of Mechanical Systems

JU –

2017

/HL

3

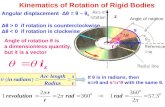
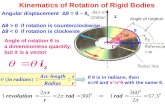
Kinetic enrgy of a rigid body

DMS6021 - Dynamics and Control of Mechanical Systems

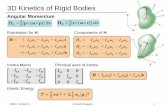
• Kinetic energy of a rigid body can be separated into:- the kinetic energy of motion of the mass center C

and - the kinetic energy of rotation of the body about C.

Let’s consider a rigid body of mass m in plane motion.

!"#!"#

$!$"#

RotT

I

ii

ii

Ivm

mrvm

xvvmvmT

Trans

2212

21

22212

21

2212

21

Δ

'';Δ

w

w

+=

÷÷÷

ø

ö

ççç

è

æ¢+=

=¢+=

å

å rω

( )[ ]xzzxzyyzyxxyzzyyxx

iiiRot

IIIIII

mrmT

wwwwwwwww

w

222

ΔxΔ222

21

2i2

1221

---++=

== åå rω

[ ]xzzxzyyzyxxyzzyyxx IIIIIIvmT wwwwwwwww 222222212

21 ---+++=

JU –

2017

/HL

4

Kinetic enrgy of a rigid bodyIf axes of coordinates coincide with the principal

axes x’ y’ z’ of the body

DMS6021 - Dynamics and Control of Mechanical Systems

[ ]2''2''

2''2

1221

zzyyxx IIIvmT www +++=

( )

221

22212

212

21 ΔΔΔ

w

ww

O

I

iiiiii

I

mrrmvmTo

=

÷÷÷

ø

ö

ççç

è

æ=== ååå !"!#$

• For a rigid body is rotating about a fixed axis through O.

[ ]xzzxzyyzyxxyzzyyxx IIIIIIT wwwwwwwww 22222221 ---++=

[ ]2''2''

2''2

1zzyyxx IIIT www ++=• In principal coordinates x’ y’ z’

JU –

2017

/HL

Conservation of Energy• Example: Let´s expresse the work of

conservative forces as a change in potential energy, the principle of work and energy becomes

2211 VTVT +=+

21

222211

θsinlg3ω

θsinmgl21ω

3ml

210

VTVT

÷øö

çèæ=

-=

+=+

0,0 11 == VT

( ) ( ) 22

22121

212

21

21

222

1222

12

321 www

w

mlmllm

IvmT

=+=

+=

qq sinsin 21

21

2 mglWlV -=-=

• Consider the slender rod of mass m.

• mass m• released with zero velocity• determine w at q

Moment of inertia of rod of length l

JU –

2017

/HL

6

KE

DMS6021 - Dynamics and Control of Mechanical Systems

4 ExampleA wheel is freely rotating about a horizontal axis O and an ideal string is wrapped on it has a small mass m attached at its end as shown. The wheel has a moment of inertia I and radius R. Find the expression for the speed of the mass after it has fallen through a distance h.

Sol.: Using energy theoremT1 + V1 = T2 + V2

0 + mgh = 𝟏𝟐m𝒗𝟐 + 𝟏

𝟐I𝝎𝟐+ 0è 𝒗 = 𝟐𝒎𝒈𝒉𝑹𝟐𝑹

(𝑰,𝒎𝑹𝟐)

m

𝝎 = v/R

m

O

JU –

2017

/HL

7

D’Alembert’s Principle4 Equilibrium equation in statics: åF = 0

è can be used to solve for three unknowns in 3D space

4 Equilibrium equation of motion in dynamics: åF = m.awhere åF is the sum of the external forces acting on the particle, m is the particlemass (constant), and a is the acc. of the particle relative to an inertial ref. frame.

Rewriting the equation of motion: åF - m.a = 0

DMS6021 - Dynamics and Control of Mechanical Systems

External forces –inertia forces = 0

Conversion of the system into a dynamics equillibriumè D’Alembert’s principle

For a body in rotational motion: åT = I.a and åT - I.a = 0

where åT is the sum of external torques acting on the body, I is the massmoment of inertia of the body wrt the rotating axis, and a is the angular acceleration of the body.The principle is applied to solve problems for a body simultaneously undergoing translation and rotation. It greatly simplifies complicated dynamic problems in mechanics.

JU –

2017

/HL

8

Virtual work and virtual displacement4 For a system of N particles

Let the position of each particle be given by x1, x2, … x3N

Let’s consider that there are 3N forces F1, F2, … F3N acting in thedirection of each coordinateLet the system at a given instant is subjected to smalldisplacements dx1, dx2, … dx3N in the direction of each coordinateWork done by the forces: dW = åFi dxi

OR, in vector notationdW = åFi dri

Note: • There is no passage of time for the displacement dx• The forces remain constant.

DMS6021 - Dynamics and Control of Mechanical Systems

Virtual displacementVirtual work

JU –

2017

/HL

9

Constraints and degrees of freedomClassification of constraints4 If a constraint can be written as an equality function of the

formf(r1, ….rn, t) = 0 orf(q1, q2, … qN, t) = 0 (where qi are generalized coordinates), then itis called holonomic constraint.

A rigid body has such types of constraints and existence ofholonomic constraints allow elimination of some variables

4 Constriants that can not be expressed in the above form arecalled non-holonomic constraints. For example, motion of agas in a container

DMS6021 - Dynamics and Control of Mechanical Systems

JU –

2017

/HL

10

Virtual work and virtual displacementClassification of constraints …4 Equality constraints involve only generalized coordinates and time

(holonomic), while non-holomonic constraints depend on generalized coordinates and higher derivatives (velocities), as well as time.

4 Inequalities do not constrain the position in the same way as equality constraints do, thus they are non-holonomic.

Other classifications4 A geometric constraint restricts the configurations that can be

achieved during motion.4 A kinematic constraint only restricts the velocities that can be acquired

at a given position. The system can, however, occupy any positiondesired

DMS6021 - Dynamics and Control of Mechanical Systems

JU –

2017

/HL

11

Virtual work and virtual displacement4 Constraints and degrees of freedom (DOF)A DOF is an important element in describing the dynamics ofa system consisting of multiple lumped parameters4 Number of degrees of freedom of a system

= the minimum number of variables to completely specify the position of every particle in the system

= Number of kinemtatically independent configuration constraintsor variables required to describe completely the motion of a system

NB: A rigid body in (unconstrained) space has 6 DOF (r,Ω)

The number of degrees of freedom of a particle/lumped mass getsreduced if it is subjected to constraints. For instance, a rigid body in a 3Dspace has 3 DOF constrained, hence its motion is defined by 3 DOF.

DMS6021 - Dynamics and Control of Mechanical Systems

JU –

2017

/HL

12

Virtual work and virtual displacement4 Constraints and degrees of freedom (DOF)4 Examples

DMS6021 - Dynamics and Control of Mechanical Systems

Rolling contact Pinned joint

(Generally only applied to a rigid body)

Fixed joint

(Generally not applied to a rigid body motion)

JU –

2017

/HL

13

Virtual work and virtual displacement4 Example

DMS6021 - Dynamics and Control of Mechanical Systems

Use the virtual work method and determine the relationship between the torque M applied to the crank R and the force F applied to the slider in the shown mechanism.

qffq

fq

ddqdd

sinsinsinsin

coscos

0mequilibriu staticin systemFor

LRLRh

LRxwhere

xFMxFW

=Þ==

+=

=+==å

( )21

21

22

2

sin1cos

sin1cos:-

-

÷÷ø

öççè

æ÷øö

çèæ-=Þ

-=

qf

ff

LR

relationtricTrigonomie

21

21

22

2

22

sin1

cossinsin

sin1cos

-

-

÷÷ø

öççè

æ÷øö

çèæ-

--=Þ

÷÷ø

öççè

æ÷øö

çèæ-+=

q

qqqdqd

qq

LRL

RRx

LRLRx

ïï

þ

ïï

ý

ü

ïï

î

ïï

í

ì

÷øö

çèæ-

+=Þ

q

qq2

2

sin1

1sin

LRL

RosFRM

gsimplifyinandngSubstituti

JU –

2017

/HL

14

Summary and Questions

DMS6021 - Dynamics and Control of Mechanical Systems

Next: Intro. generalized coordinates, derivation of Lagrange's equation from D’ Alembert’s principle.

In this lecture we focused on KE of a rigid body, a.o.4 Kinetic energy of rigid bodies: Transilation and rotation KE4 KE of rigid body when coordinates of motion coincide with

the principal axes of the body4 Concept of virtual work and virtual dispalcement4 DOF and classification of constraints4 D'Alembert's Principle

?