i

Figure 1. The Cartesian coordinate system for 3-dimensional Euclidian space.

Chapter II: General Coordinate Transformations

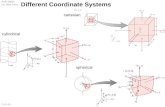
Before beginning this chapter, please note the Cartesian coordinate system belowand the definitionsof the angles θ and φ in the spherical coordinate system. In the spherical coordinate system, (r,θ,φ)we shall use:

and in the cylindrical coordinate system (ρ,φ,z):

x = r sinθcosφy = r sinθsinφz = r cosΘ

x = ρ cosφy = ρ sinφ

ρ2 = x2 + y2 .

II-1

dx i�

�f i

�q 1dq 1 �

�f i

�q 2dq 2 �

�f i

�q 3dq 3

��j�x i

�q jdq j

also�

�x i��k

�q k

�x i

�

�q k

using chain rule

dx i�

�x i

�q jdq j

� A i.j dqj

�

�x i�

�q j

�x i

�

�q j�Bi .

j �

�q j

Chapter II: General Coordinate Transformations

Consider two coordinate systems in 3-dimensional Euclidian space:

1. a Cartesian system where a point is specified by (x1, x2, x3) � (x,y,z)

2. a general "qi" system where a point is specified by (q1, q2, q3).

Each point (x1, x2, x3) corresponds to a unique set of real numbers (q1, q2, q3). Further, each xi is a function of the qj,fi (q1,q2,q3), and each qj = hj (x1,x2,x3) where all first partial derivatives of fi and hj exist. Using only the chain rulefor differentiation, the following equations can be obtained:

where we have used the notation x i (q1,q2,q3) � f i (q1,q2,q3) and q j(x1,x2,x3) � hj(x1,x2,x3) .

Note that the differential, dxi, "transforms with" [ �xi/�qj ] and the partial derivative "transforms with" [ �qj/�xi].So, using the summation notation (repeated indices ==> summation):

Note the placement of the indices.

II-2

Ai.j ��x i

�q j� contravariant transformationmatrix

.

Bi.j�

�q j

�x i� covariant transformationmatrix

dx

dy

dz

�

dx 1

dx 2

dx 3

�

sin�cos� rcos�cos� �rsin�sin�

sin�sin� rcos�sin� rsin�cos�

cos� �rsin� 0

dr

d�

d�

dr

d�

d�

�

dq 1

dq 2

dq 3

In general, �xi/�qj � �qj/�xi. This means that dxi and �/�xi transform differently under the

coordinate transformation. The two transformations have been named contravariant and covariant,respectively.

Example: Transformation from Cartesian to spherical coordinates:

x = rsinθcosφ � x1 r = [x² + y² + z²]½ � q1

y = rsinθsinφ � x2 θ = cos-1(z/r) � q2

z = rcosθ � x3 φ = tan-1(y/x) � q3

The differentials are given by:

dx = sinθcosφ dr + rcosθcosφ dθ + -rsinθsinφ dφdy = sinθsinφ dr + rcosθsinφ dθ + rsinθcosφ dφdz = cos θ dr + -rsinθ dθ + 0 · dφ

Thus,

II-3

dq k'

Mq k

Mx jdx j

' [A &1]k.j dxj

M

Mq n'

Mx m

Mq n

M

Mx m' [B &1]n.

m M

Mx m

In the above equation A11 = sinθcosφ and A3

2 = -rsinθ, etc. The elements of the contravariant transformationmatrix are obtained from the expression for the differentials of dx, dy and dz.

One can also show that:

drdd

r r rr r

dxdydz

θθ ϕ θ ϕ θ

θ ϕ θ ϕ θϕ θ ϕ θ

= −−

⋅

sin cos sin sin cos(cos cos ) / (cos sin ) / sin /sin / ( sin ) cos / ( sin ) 0

And using the chain rule one finds:

Note that My/Mθ = rcosθsinφ is not simply related to Mθ/My = (cosθsinφ)/r. One can see also from the above

equations that A-1 = BT and B-1 = AT. In the above expressions different summation indices were used foreach of the sums. This is a good habit to adopt. Try to do this in all your derivations.

Sometimes you will find the notation: Aij for Bi

j. We won't use this notation since it is

confusing. Keep in mind that Ai j … Ai

j. If you don't understand this comment look again carefully at the indiceson the above equations.

Exercise: Evaluate the A (contravariant) matrix for the transformation (from Cartesian to sphericalcoordinates) if r = 3, θ = π/4 and φ = π/2.

Exercise: Find the A-1 matrix for the same values of r, θ, and φ in the above exercise.

II-4

V i� A i.j V '

j

contravariant vector transformation

Vk � Bk.n V 'n

covariant vector transformation

Rules for keeping track of indices:1. Always use different index symbols for different summations;2. Indices on the left side of the equation match with the "left-most" index on the right hand side;3. "Superscripts" found in the "denominator" (such as the k in �/�xk) function as subscripts in the expression;

4. Aij and Bk

m have four "positions", two "upper" and two "lower" (see below);

5. A "left" position on Aij or Bk

m denotes a row index; the "right" position denotes column index;6. Indices are always "matched" in an equation (look for the pairs);

left index denotes a matrix "row"

i j k

m

right index denotes a matrix "column"

Contravariant and covariant vectors:A triplet of quantities in the Cartesian system, (V1,V2,V3), [such as (dx1,dx2,dx3) ] which transforms into its

counterpart, (V'1,V'2,V'3), in the qi system [such as (dq1,dq2,dq3)] via the Aij matrix is said to be a set of

contravariant vector components. Contravariant vector components are denoted by superscripts.

A triplet of quantities in the Cartesian system, (V1,V2,V3), [such as (�/�x,�/�y,�/�z) ] which transforms into its

counterpart, (V'1,V'2,V'3), in the qi system [such as (�/�q1,�/�q2,�/�q3)] via the Bkm matrix is said to be a set of

covariant vector components. Covariant vector components are denoted by subscripts.

II-5

The differentials, dxi, transform like contravariant vector components under a generalized (linear) coordinatetransformation. The "linear" means that the transformation is linear in the differentials. The partial derivatives,�/�xk, transform like covariant vector components under a generalized (linear) coordinate transformation. In fact,any triplet which transforms "like the differentials" under a generalized linear coordinate transformation is said to bea contravariant vector. A triplet which transforms "like the partial derivatives" is said to be a covariant vector underthe generalized linear coordinate transformation.

Later we shall find out how to find the proper contravariant and covariant components of a physical vector. Two"physical" vectors are always simple to deal with: dr and �f(x,y,z).

----------------------------------------------------------------------------------------------------------------------Exercise: Find the contravariant components of the vector dr in the Cartesian coordinate system.

Exercise: Find the contravariant components of the vector dr in the spherical coordinate system.

Exercise: Find the covariant components of the vector � � x i (�/�xi) in the spherical coordinate system.

Exercise: Find the covariant components of the vector � � x i (�/�xi) in the cylindrical coordinate system.

II-6

Kronecker Delta Symbol and Other Notation

The Kronecker delta symbol is � i j = { 0 if i � j and 1 if i=j}.

Generalized Kronecker delta:+* 0 if any two superscripts (or subscripts) are equal* or if {i,j,k,...m} � {i',j',k',...m'}

i j k, .. . m i' j' k', ... m' = * +1 if subscripts are even permutation of superscripts

* -1 if subscripts are odd permutation of superscripts.

Examples: 123 132 = -1

123 312 = +1

122 132 = 0

Numerically, ij = ij = ij. But in an expression, these can carry different information.

PERMUTATION SYMBOLS (COMPLETELY ANTISYMMETRIC "TENSORS")

+ijk..m � ijk...m

123...n = * 0 if any two superscripts are equal* or if superscripts are not same set as 1,2,3...n* +1 if the superscripts are an even permutation of 1,2,3,...n* -1 if the superscripts are an odd permutation of 1,2,3,...n.+

ijk...m � ijk...m123...n = * 0 if any two subscripts are equal

* or if subscripts are not same set as 1,2,3...n* +1 if the subscripts are an even permutation of 1,2,3,...n* -1 if the subscripts are an odd permutation of 1,2,3,...n.

The above symbols are special cases of the generalized Kronecker delta and are often used with expressionsinvolving permutations. The above symbols are "almost" tensors as we shall see in the chapter on tensors.

Examples: 123 = 312 = 231 = +1213 = 132 = 321 = -1112 = 223 = 323 = 0, etc.

123 = 312 = 231 = +1213 = 132 = 321 = -1313 = 322 = 211 = 0, etc.

Example: 1234 = +10123 = 0

II-7

ds² � gjk dqj dq k

.j,k .summation impliedg � metric tensor

The Metric Tensor

The metric tensor, gjk, for the qi system is defined as follows:

where ds² = (dx)² + (dy)² + (dz)² = dxidxi (summation over i implied)

What is gjk ?

ds² = dr·dr = dxidxi

= [�xi/�qj]dqj · [�xi/�qk]dqk Summation over i

= [�xi/�qj] [�xi/�qk] dqj dqk Summation over i

= gjk dqj dqk

Thus gjk = [ �xi/�qj ] [�xi /�qk ] (Summation over i)

The metric tensor is symmetric since

[�xi/�qk] [�xi/�qj] = [�xi/�qj] [�xi/�qk] = gkj = gjk. Summation over i

THE METRIC TENSOR IN CARTESIAN SYSTEMS:

dxi = [R-1]i k dx'k = [�xi/�x'k] dx'k

Thus gjk = �i [R-1]i j [R-1]i k

= �i [R-1]T j i [R-1]i k

= �i Rji [R-1]i

k

= �i [RR-1]jk = 1jkand gcartesian = 1

II-8

The metric tensor, g = ATA

gspherical �

........ ........ ........

........ ........ ........

........ ........ ........

The Jacobian:

Jacobian � det [ � qi / �xj ] = det [Bj i ] = det(B)

where [�qi/�xj] implies a matrix whose i,j component is �qi/�xj.

proof:

gjk = �i [�xi/�qj] [�xi/�qk]

= �i Ai j Ai

k

= �i [AT]j iAi

k= [ATA]jk.

Exercise: Find g for the spherical coordinate system.

II-9

Exercise: Find the metric tensor for a qi system if

ds² = 4dq1dq1 - q2 dq1dq2 + π dq2dq3 + 7q1 dq2dq2 - dq3dq3.

Exercise: Find the metric tensor for the cylindrical coordinate system:

x = ρ cosφ ρ = [x²+y²]½

y = ρ sinφ φ = tan-1[y/x].z = z

II-10

� �

qqq

qx

x1q

no sum on i

qqx

ii

i

i

kk

ki

ii

j

2

j

1 / 2

� �

��

��

�

� �

�

�

�

�

�

�

The unit vectors, qi in the qi system

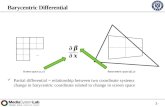
The equations qi = qi(x1,x2,x3) = ci where i = 1,2,3 each represent a surface of constant qi in the threedimensional space. Below is a schematic of three such surfaces which intersect at a point. This point can belabelled by its (x,y,z) value, or by (q1,q2,q3) = (c1,c2,c3).

Unit vectors perpendicular to a surface of constant qi can be obtained from the �qi:

Note that qi = Bj i x j / [βi] (with no sum on i !) where βi � | �qi |.

Later we shall put the βi into another more convenient form.

Exercise: Find r, θ, and φ in the spherical coordinate system.

II-11

answers: r = sinθcosφ x + sinθsinφ y + cosθ zθ = cosθcosφ x + cosθsinφ y - sinθ zφ = -sinφ x + cosφ y

The Inverse Metric Tensor

Claim: g-1 = BTB.

proof:

1. We note from page II-2 that expression a) below holds; from page II-3 we find expression b):

a) [�qk/�xj] = Bj k .

b) [�qk/�xj] = [A-1]k j.

Thus BT kj = [A-1]k j and BT = A-1.

2. But g-1 = [ATA]-1 = A-1 [AT]-1 = BT B

where we have used [AT]-1 = [A-1]T = [BT]T = B. (to be shown later).

Note that [g-1]jk = �n [BT]j n Bnk .

II-12

gij � metric tensor components.

g ij� inverse metric tensor components

The components of the inverse metric tensor, g-1, are denoted by gi j -- with superscripts! Later we shall

see that the superscripts on g-1 and the subscripts on g have definite implications. Normally, one does not use aspecial symbol for the inverse metric tensor -- when written with components.

Claim: βi � |�qi| = �gii (no sum on i).

proof:

1. gii (no sum on i) is the diagonal (ii) component of the inverse metric tensor.

gii = [BTB]ii = [A-1]ik Bk

i sum on k, no sum on i.

= Bk i Bk

i sum on k only.

= [�qi/�xk] [�qi/�xk] sum on k only.

= [ (�qi/�xk) xk] · [ (�qi/�xn) xn] = �qi · �qi ( no sum on i).

= (�qi/�xk) (�qi/�xn) xk· xn = (�qi/�xk) (�qi/�xn) δkn

2. Thus gii = �qi·�qi= |�qi|² no sum on i.

3. So, βi = |�qi| = �gii (no sum on i).

II-13

B T ik � A �1 i

k � B ki

A Tnm

� B �1nm

� A mn

dxi � [gx]ij dxj and dqk � gkm dq

m

Use of g to convert from contravariant to covariant components

Claim:

proof:

1. let dxj = Aj n dqn ; multiply on the left by [gx] ij � [gcartesian]ij = 1ij and sum over j:

[gx]ijdxj = [gx]ij Aj n dqn = [gx]ij Aj

n δnn' dqn'

= [gx]ij Aj n [g-1g]n

n' dqn' where 1 is replaced by g-1g and g is for qi system.

= [gx]ij Aj n gnm gmn' dqn' (recall that superscripts ==> g-1)

2. Now use g-1 = BTB:

[gx]ijdxj = [gx]ij Aj n [BTB]nm gmn' dqn'

= δij [ABTB]jm gmn' dqn'

= [ABTB]im gmn' dqn' = [AA-1B]i

m gmn' dqn'

= Bim gmn' dqn'

= Bim [gmn' dqn']

3. Thus [gx]ijdxj � dxi and [gmn' dqn'] � dqm transform like covariant vectors and dxi = Bim dqm .

QED

Note that we have defined the dx i and dq m in terms of dxj and dqn'.

II-14

claim g is diagonal iff

(diagonal g <==> orthogonal coordinate system)

i j

q q:� �

� �ij

�

The previous proof can be used to show that for any vi in the Cartesian system, the proper covariant vector

components can be formed from vi = [gx]ij vj -- and in the qk system,

v'm = gmn' v'n'.-------------------------------------------------------------------------------------------------------------------------------------------

Exercise: Show that v'n = gnk v'k.

-------------------------------------------------------------------------------------------------------------------------------------------

proof:

1. case I: show that qi· qj = δij ==> g is diagonal.

a) assume qi· qj = [�qi/�gii]·[�qj/�gjj] no sum on i or j = δij b) thus,

�gii�gjj δijno sum on i or j = δijgii = �qi·�qj (no sum on i)

= [�qi/�xk] xk ·[�qj/�xn] xn

= Bk i Bn

j δkn

= BTi k Bn j δkn

= [BTB]ij

= [g-1]ij

c) so δijgiino sum on i = [g-1]ij and g-1 is diagonal.

d) if g-1 is diagonal, g is also.

2. case II: assume g is diagonal and show qi· qj = δij.

a) g-1 is diagonal if g is.b) but,

[g-1]ij = [BTB]ij = Bk i Bn

j δkn = �qi·�qj (all the steps in case I are reversible) c) therefore (since steps in case I are reversible):

[g-1]ij = δijgiino sum on i ==> �qi·�qj = δij C , where C = constant.

II-15

The u�j and u�i basis vectors for the qk system

x un n

i

i

A� �

�

Claim: If A is orthogonal g = 1.

proof:

1. AT = A-1 since A is orthogonal.

2. thus, ATA = g = A-1A = 1.

Claim: �gii qi no sum on i � ui transforms into xk via A.

proof:

1. �gii qi no sum on i = Bk i xk (see box on page II-10 and βi on page II-12).

2. so, ui = Bk i xk = [BT]i k xk = [A-1]i

k xk; multiply both sides by An i and sum over i:

An i ui = An i [A-1]i

k xk = [AA-1]n k xk.

= δn k xk = xn.and,

Since the ui and xn transform "according to" A we can (using same steps as on page II-13) show that:

u�j = gji u�i

gives the corresponding basis "vectors" which transform according to B:

xk = Bk j u�j.

The uj and ui vectors serve as basis vectors -- playing the "role" of xk and xn in the "general" coordinate system. We shall show on the next page that these generalized basis vectors obey an orthogonality condition and their dot

products can be determined from the metric tensor, g. The geometrical interpretation of the uk and un vectors canbe seen from a simple example, after we derive the special conditions on the next page.

II-16

ui � uj � gij

u i · u j� g ij

u i ·u j � �i

j

Orthogonality anddot products for"basis vectors".

derivations:

1. u� i· u�j = [B-1]ik xk · [B-1]j

n xn

= [AT]ik [AT]j

n xk·xn

= [AT]ik An

j δkn

= [AT]ik Ak

j sum over k

= [ATA]ij = gij.

2. u�i · u�j = [A-1]i k xk · [A-1]j n xn

= [BT]i k Bn j xk · xn

= [BT]i k Bn j δkn

= [BTB]ij

= gij.

3. u�i· u�j = [A-1]i kx k · [B-1]j

n xn

= [A-1]i k [AT]j

n xk·xn

= [A-1]i k [AT]j

n δk n

= [A-1]i k Ak j

= [A-1A]i j

= δi j.

II-17

[ When bold face is not available, use ^ and ----- (bars) over symbols to denote vectors.]

Derivations:

1. F = f1q1 + f2 q2 + f3 q3 = �ifiqi where fi � ordinary components of F

2. Substitute ui = �gii qi no sum on i in above.

F = �i fiqi = �i fi [ ui/�gii]

= �i [fi/�gii] ui

3. F·uj = �i [fi/�gii] ui·uj

= �i [fi/�gii] δij

= [fj/�gjj]. no sum on j

On the following page we shall show that F·uj = F'j, and transforms like the covariant component of F.(Note that in the qi system, the components are distinguished from those in the Cartesian system by primes.) Once

this is accomplished, we can find the contravariant component of F, F' k, from F' k = gk n F'n.

Ordinary (�f i ) , contra- and co-variant components of F:

F = f 1 q 1+f 2 q 2 +f 3 q 3

F = F � i u� i

F = F � j u� j

F �i = F � u� i and F � k = F � u� k

II-18

F·uj � F 'j� covariant component of`F in q i system

F·u k� F 'k � contravariant component

Claim:

proof:

1. F = Fi xi = fn qn = (fn/�gnn)un ; dot with xj.

2. Fi xi· xj = (fn/�gnn) un·� xj transform un (see page II-15)

Fj = (fn/�gnn) [A-1]nkxk � xj

= F·un [BT]nk δk

j (see p. II-17 )

F· xj = Bjn F·un

4. So F·un and F· xj are covariant components of F (they transform via B).

.......

Claim:

proof:

1. First note that F·uk = [F'n un]·uk = F'n gnk (see page II-16)

2. Consider Fk = Bkn F'n and multiply by [gx]kj and sum over k

3 Fk[gx]kj = [gx]kj Bkn δn

n' F'n'

= δkj Bkn [gg-1]n

n' F'n'

= δkj Bkn gnm gmn' F'n'

= δkj Bkn �i[AT]n

iAim gmn' F'n' use AT = B-1

= �i[BB-1]ji Aim [gmn' F'n'] =Aj

m [gmn' F'n'].

so gmn' F'n' and Fk[gx]kj transform via Ajm and are contravariant components of F.

II-19

F � F 'k uk

� F ' j u j

F·F � F 'j F 'j

Fi Fi� F 'k F '

k

....

Derivation:

1. F = fn qn = (fn/�gnn) un = (F·un)un = F'nun ----as shown on p. II-18.

2. = gnm F'm un = F'm [gmn un] = F'm um .

Derivation:

1. F·F = F'i ui · F'k uk = F'i F'k δik = F'i F'i.

.......

Derivation:

1. F · F = FiFi = Bim F'm Ai

k F'k

= [A-1]mi Ai

k F'm F'k = [A-1A]mk F'm F'k

= δmk F'm F'k

= F'k F'k

II-20

g �

6 2 �5

2 3 2

�5 2 10

Exercises:

1. Assume that in the s,t,w ( � q1,q2,q3 ) a physical quantity is given by F = 6u1 + 4u3. Find the contravariant

components of F in the s,t,w system (leave answer in terms of s,t,w).

2. Given that for the s,t,w system g is as shown,

find the covariant components of F in the stw system. Leave answer in terms of s,t,w.

3. Find FiFi (note unprimed components ==> xj system).

4. Find u1·u3.

II-21

A �1�

3 �32

3/2 0

3/2 3 �32

0

0 0 5

; g �1� B TB �

9 9 �32

0

9 �32

9 0

0 0 25

; g �

49

�2 �39

0

�2 �39

49

0

0 0 125

Covariant FormWhen expressions are written totally in terms of covariant and contravariant vector components with proper

summation over all indices (such as FiFi) they can be easily evaluated in either (x,y,z or the qi) system. Further,one can set the expression for the quantity in, say, the xyz system equal to the expression in the expression in terms

of the qi. This is a powerful tool. It means you don't have to use A (or B). This is used extensively in specialrelativity and in general relativity. It can also be of use in any problem where one wants the answer, say, in the xyzcoordinate system, but finds it easier to use a coordinate system which follows fluid flows, or isobars, etc.

A Physical Picture of the Coordinate Systems1. assume that s � q1 = 3x·cosα + 3y·sinα

t � q2 = 3x·cosβ + 3y·sinβw � q3 = 5z

2. Let α = π/6 and β = π/3 to simplify the problem.

s = 3x(�3/2) + 3y/2t = 3x(1/2) + 3y(�3/2)w = 5z

You can determine A-1 = BT and g-1 = BTB easily:

3. Note that s · t = u1/�g11 ·u2/�g22 = (1/9)·9·�3/2 = �3/2 =/ 0.

also, u1 = 3 s ;u2 = 3 t; and u3 = 5 w. u1 = g1mum

II-22

Note easiest way to find covariant and

contravariant components of F:

1) "pick off" F'j as the coefficients of u j in

the expression for F.

2) find F' k from g k jF'j.

u q

u u

i ii i

k kj

j

gg

� �

� �

�

�

no sum on i

Exercises:1. Find the ui ( i = 1,2,3) in the spherical coordinate system in terms of r,θ. and φ.

2. Find covariant and contravariant components of the position vector, r, and dr, in the spherical coordinate system.Leave answer in terms of r,θ,φ and dr, dθ, dφ. Hint for dr: recall how dqi are related to the definition ofcontravariant components.

II-23

F xF y

F z

AFFF

�

�

�

�

�

����

�

�

����

��

�

��

�

�

��

�

�

�

'

'

'

1

2

3

F xF y

F z

�

�

�

�

�

����

�

�

����

�

�

�

�������

�

�

�������

�

�

����

�

�

����

�

�

�

��

�

�

��

�

�

�

3 32

32

0

32

3 32

0

0 0 5

23

43

0

3 21 2 3

0

Use of A and B to find F·xi

The components of F in the xyz system can be obtained from the F'k using A, or from the F'j using B:

Example: Find F· xi if F = 2 s + 4 t in the example on page II-21.

First, find the F'j: F = 2/�9 u1 + 4/�9 u2 so F'1 = 2/�9 and F'2 = 4/�9. Then use B = [A-1]T to relate thecovariant components in the xyz and stw system:

Exercise: In the above example, find F'k.

II-24

det M � � i j k m1im2jm3k

The Determinant in Summation Notation

detM = * m11 m12 m13 ** m21 m22 m23 ** m31 m32 m33 *

= (-1)(1+1)m11(m22·m33 - m23·m32) + (-1)(2+1)m21(m12·m33 - m13·m32) + (-1)(3+1)m31(m12·m23 - m13·m22)

= � i � j � k m 1 i m 2 j m 3 k · {"sign factor"} --Note six terms for which i,j, and k are all different.

Thus the εijk symbol can be used to form a concise summation notation for detM.

Exercise: Write the determinant of g in summation notation.

Exercise: Write *g-1* in summation notation. Hint, use εijk rather than εijk.

Exercise: Write [*A* A-1 ] i k in summation notation.

sign factor = +1 for ij k even permutation of 123 -1 for ij k odd permutation of 123 0 otherwise

= �i j k

II-25

�i j k � i m n� �j

m�kn� �j

n �km

Exercise: Write out the terms in εknmεkji gnm gji and try to find the simplest final result.

Exercise: There is a "similar" expression (to that in the box on page II-24) for the determinant of a 4x4 matrix, using εijkm. Using what you know about determinants write down what you think it should be.

--------------------------------------------------------------------------------------------------------------------------------- An interesting "expression" for εijk is:

* δi1 δj

1 δk1 *

εijk = * δi2 δj

2 δk2 *

* δi3 δj

3 δk3 *.

= [ δi1δj

2δk3 + δi

2δj3δk

1 + δi3δj

1δk2 ] - [ δi

1δj3δk

2 + δi2δj

1δk3 + δi

3δj2δk

1 ]|| ||

3 even perm. 3 odd perm.

A word of warning: in Cartesian systems one can use εijk and εijk in an "equivalent" way. But in the generalcoordinate system care must be taken. In strict covariant notation, these symbols are usually accompanied by either�|g| or 1/�|g|. In Cartesian systems, since |g|= 1, one cannot see the distinction. We shall discuss this later.

II-26

� � � u j� 'j�

.where we define

� 'j ��

�q j

Vector Operators in Covariant Form

1. The gradient, � φ

� φ = xk �φ/�xk

= Akj u

j Bkm �φ/�qm

= Akj [A-1]m

k �φ/�qm uj

= [A-1]mk Ak

j �φ/�qm uj

= [A-1A]m j u

j �φ/�qm

= δm j u

j �φ/�qm

= uj �φ/�qj

Exercise: Find � φ(r,θ,φ) in spherical coordinates, as a function of r, θ, φ and r, θ, and φ only.

Exercise: Find � φ(ρ,θ,z) in cylindrical coordinates, as a function of ρ, θ, z and ρ, θ, and z only.

II-27

½ g i �� 'j gi � � Bk

i� 'i A k

j

2. The Divergence, �·F.

1. �·F = xk�k · xnFn = �kFn xk· xn

= �k Fn δkn = �kFk

= (Bki �'i) (Ak

j F'j) Note that �'i acts on all that follows.

= Bki Ak

j �'i F'j + Bki F'j �'i Ak

j

= [A-1]ik Ak

j �'i F'j + F'j { Bki�'i Ak

j}

= [A-1 A]ij �'i F'j + F'j { Bk

i�'i Ak

j}

= δij �'i F'j + F'j {............}

= �'i F'i + F'j {............}

2. We now derive three relationships which will be used to evaluate {............}.

a) First note that (see page II-12 for gi� in terms of derivatives)

½gi� � gi� /�qj = ½[�m (�qi/�xm)(�q�/�xm)] �/�qj [�n (�xn/qi)(�xn/�q�)] sum over i and � implied!

= ½ �m,n (�qi/�xm)(�q�/�xm) [ (�²xn/(�qi�qj))(�xn/�q�) + (�xn/�qi)(�²xn/(�q��qj)) ] rearrange terms:

= ½ �m,n [ (�qi/�xm) (�²xn/(�qi�qj)) (�xn/�q�)(�q�/�xm) + (�q�/�xm)(�²xn/(�q��qj)) (�xn/�qi)(�qi/�xm)]

= ½ �m,n [ (�qi/�xm) (�²xn/(�qi�qj)) (�xn/�xm) + (�q�/�xm)(�²xn/(�q��qj)) (�xn/�xm)]

= ½ �m,n [ (�qi/�xm) (�²xn/(�qi�qj)) δmn + (�q�/�xm)(�²xn/(�q��qj)) δm

n] -- use δmn to do n sum

= ½ �m [ (�qi/�xm) �'i (�xm/�qj) + (�q�/�xm)�'�(�xm/�qj) ] i, � dummy indices ==> add terms

= �m [ (�qi/�xm) �'i (�xm/�qj)

= Bmi �'iAm

j = Bki �'iAk

j so,

and {.............} = ½gi� �'j gi� .

II-28

� ·F �

1�g

� 'i [�g F 'i ]

b) Next we consider detg � g = gik [gcof]ik sum on k, no sum on i: i can be 1,2,or 3.

Since gik is symmetric and detg = detgT = g, [gcof]ik = [gcof]ki. Thus,

�g/�gik = [gcof]ik

c) Also, we know that,

[g-1]ik = [gcof]T ik/g, note: g � detg

gik = [gcof]ki/g,

= [1/g] �g/�gki = [1/g] �g/�gik using result above for cofactor.

= � [ln g] /�gik

3. Finally, using the results in 2 a), b), and c):

F'j {.........} = F'j [½ gi� �'j gi� ] note sums on i, �, j

= F'j [½ (�[ln g]/�gi�) (�gi�/�qj) ]

= F'j [�(ln�g)/�qj]

= F'j [(1/�g) (��g/�qj)]

4. So,

� · F = [�g/�g] �'i F'i + F'j [(1/�g) � �g/�qj] = (1/�g)[�'i �g F'i]

and,

II-29

Exercise: Find �·F in the spherical coordinate system, using the generalized formula. Put answer in terms of r,θ,

φ and r, θ, φ . Use F = fr r + fθ θ + fφ φ.

Exercise: Repeat the above exercise for the cylindrical coordinate system.

Exercise: Given �g = st(sinw) in the s,t,w (� q1,q2,q3) system, find �·F for F = [st/w²]u1 + [(sinw)/t]u2 -wu3.

II-30

1�g

� 'k [�g g kj� 'j � ]

3. The Laplacian, �·� φ = �²θ.

�·� φ = �· [�φ] use form for divergence and gradient:

= �·[uj�'jφ] = �·[ uk uk·(uj�'jφ) ]

= [1/�g]�'k [�g uk·uj�'jφ] note contravariant components of �φ

= [1/�g] �'k [�ggkj�'jφ]

Exercise: Find �²[r²esinθ] by working totally in the r,θ,φ system.

II-31

ε i j k

�gx� A i

�A j

m A knε '�mn

�gwhere gx � xyz system metric tensor

4. The Curl, � x F

1. Before deriving the general expression for the curl, we need to consider how εijk "transforms" under the generalized coordinate transformation.

Claim:

Derivation:

Note that gx � metric tensor in the Cartesian system and gx � |gx| = 1. Consider the following:

εijk |A|= Ai� Aj

m Akn ε'�mn =+(-)|A| if ijk is cyclic (non-cyclic)

= 0 if ijk is not a permutation of 123.

where ε'�mn is numerically equal to ε�mn

and εijk = Ai� Aj

m Akn ε'�mn |A|-1

= Ai� Aj

m Akn ε'�mn/ |A|

= Ai� Aj

m Akn ε'�mn/ [|AAT|]1/2

εijk /�gx = Ai� Aj

m Akn ε'�mn/�g

where one notes that in all cases ( e.g., when |A| <0 ):

�g � |A|2. To derive the form for the curl, start in the Cartesian system:

�xF = x[�2F3 -�3F2] + y[�3F1 -�1F3] + z[�1F2 -�2F1]

= ε123 x1�2F3 + ε132 x1�3F2 + ε231 x2�3F1 +ε213 x2�1F3 + ε312 x3�1F2 + ε321 x3�2F1

= εijk xi�jFk

= [1/�gx]εijk xi�jFk where gx = 1.

That is, the curl can be written like a determinant.

II-32

F G x F G

x F G

ijk

i j k

lmn

l m n

� �

�

�

�

�

�

Cartesian systems only

In fact, any cross product in the Cartesian system can be written like a determinant:

3. Now we transform the "determinant" form of the curl:

� x F = εijk xi �j Fk = [1/�gx] εijk xi �j Fk

= [1/�g]Ai� Aj

m Akn ε'�mn Bi

rur Bjs �'s Bk

t F't

= [1/�g] Bir Ai

� Bj

sAjm Bk

tAkn ε'�mn ur �'s F't + {...�'sBk

t....}

= [1/�g] [A-1T]ir Ai

� [A-1T]j

sAjm [A-1T]k

tAkn ε'�mn ur �'s F't + {.....}

= [1/�g] [A-1]ri Ai

� [A-1]s

jAjm [A-1]t

kAkn ε'�mn ur �'s F't + {...}

= [1/�g] [A-1A]r� [A-1A]s

m [A-1A]tn ε'�mn ur �'s F't + {....}

= [1/�g] δr�δs

mδtn ε'�mn ur �'s F't + {....}

= [1/�g] ε'�mn u� �'m F'n + {....}

where we shall next show that the second term, {.......} = 0.

4. {....} = [1/�g] Bir Ai

� Bj

sAjm Ak

n ε'�mn ur F't �'s Bkt

= [1/�g] δr�δs

m Akn ε'�mn ur F't �'s Bk

t

= [1/�g] δr�δs

m ur F't ε'�mn Akn �'s Bk

t

= [1/�g] u� F't ε'�mn Ak

n �'m Bkt

= [1/�g] u� F't ε'�mn (�xk/�qn) �'m (�qt/�xk)

II-33

� x F � [1/�g] � ' i j k ui � ' j F 'k

(general q i system )

{...} = [1/�g] u� F't ε'�mn [�/�qm (�qt/�xk)(�xk/�qn) - (�qt/�xk)�/�qm(�xk/�qn)]

= [1/�g] u� F't ε'�mn [�/�qm( �qt/�qn ) - Bk

t �/�qm(�/�qn)xk]

= [1/�g] u� F't ε'�mn [�/�qm(δt

n ) - Bkt �'m �'n xk]

= [1/�g] u� F't ε'�mn [ 0 - Bk

t �'m �'n xk]

= -[1/�g] F't Bkt ε'�mn u

� �'m �'n xk

= [1/�g] F't Bkt ε'�nm u

� �'m �'n xk since ε'�mn = - ε'�nm

= [1/�g] F'n Bkt ε'�nm u

� �'n �'m xk since �'m�'n = �'n�'m

= [1/�g] F'n Bkt ε'�mn u

� �'m �'n xk since m and n are dummy indices.

= 0 (note: we showed {...} = - {...} so {...} = 0)

Thus,

Note:

εijk xixjFk = 0 ==> (rxr)·F = 0

εijk �i�jFk = 0 ==> (�x�)·F = 0 if the � operators do not act on a function following F.

εijk Fixjxk = 0 ==> F·(rxr) = 0

In general, in an expression involving εijk or εijk:

if the remainder of the expression is symmetric under the interchange of any two of the indices ijk then the totalexpression is zero. No conclusion can be made if the remainder of the expression is antisymmetric under theinterchange of two indices.

II-34

L x F ' [1//g] /0000000

u1 u2 u3

L '1 L '2 L '3

F '1 F '2 F '3

/0000000

Writing the curl as a determinant can sometimes make a calculation easier:

Transforming the general expression for the curl using the metric tensor:

1. First, we note that:

ε'ijk |g-1| = giR gjm gkn ε'Rmn = gRi gmj gnk ε'Rmn

where ε'Rmn is equal numerically to εRmn

ε'ijk = gRi gmj gnk /|g-1| ε'Rmn

2. Thus starting with the general form given on page II-33,

L x F = [1//g]ε'ijk ui L'j F'k use the form for ε'ijk given above,

= [1//g] gRi gmj gnk /|g-1| ε'Rmn ui L'j F'k

= [1//g] /|g-1| ε'Rmn gRi gmj gnk ui L'j F'k

= [1//g] g ε'Rmn uR[ L'm gnkF'k - F'kgmjL'jgnk]

since |g-1| = 1/g

= [1//g] g ε'Rmn uRL'm F'n - {[1//g] g F'k ε'Rmn uR gmjL'jgnk]}

… /g ε'Rmn uR L'm F'n

note that L'm = gmi L'i … L'm and L x F … /g ε'Rmn uR L'm F'n

II-35

� '�mn �

g�i gmj gnk

|g |� ' i j k

.

�i j k �Bi

�BjmBk

n

|B |� '

�mn

.

�i j k�

A i�A j

mA kn

|A |� '�mn

g �

7 0 �10 3 0�1 0 4

; g �1�

181

12 0 30 27 03 0 21

In general,

F x G = �g ε'�mn u� F'm G'n = [1/�g]ε'ijk ui F'j G'k

W·(F x G) = um W'm · [1/�g]ε'ijk ui F'j G'k = [1/�g]ε'ijk Wi F'j G'k (recall um·ui = δmi)

Exercise care with such formula when any vector is replaced by �.Some other expressions which might be useful:

Exercise:

In the stw coordinate system where g and g-1 are given by

and F = s²tw s -t²sw t+ ln(stw)w find u1·�xF.