1

The Wave Equation for transverse waves: summary → Sum forces on a small piece of a continuous body

(in this case a string)

2

2

22

2 1ty

vxy

∂∂=

∂∂

yx

WAVE EQUATION(for a stretched string)

the solution for normal modes

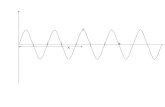
( ) ( ) txftxy ωcos, =

1

21

ωµ

πω nTL

nn =⎟⎟

⎠

⎞⎜⎜⎝

⎛=

( )n

xAxfλπ2sin=

( ) txAtxy nn

n ωλπ cos2sin, =

(called stationary waves, standing waves, or resonances - where ω is the same for all points along string)

evaluating thisusing BCs for a string fixed both ends

along the way:

mass/ length

frequency of normal mode or standing wave on stringNM amplitude

The y position at any point x along a string and at time t

∴ final solution for standing waves on a string:

WAVE FUNCTION for standing waves (normal modes) of a string!

Amplitude along the string at any point x

Normal mode frequency

This holds for BC of f(x) =0 at each end of the string

For transverse waves

2

Week 7 Lecture 3: no problems for this lecture

Normal Mode solutions to the wave equation – Longitudinal waves

So far we have developed the Wave equationfor a transverse wave on a string

Solution for normal modes (wave function) for transverse waves on a string with both ends fixed.

We still have to look at the travelling wavesolution, but first we should look at the other type of wave that can propagate in an elastic medium

Longitudinal wavesWe will have to start again by developing another wave equation for these kinds of waves. Fortunately the procedure is the same as before, and the result also similar.

3

The Wave Equation for Longitudinal Waves→ So far we have only considered transverse waves,

where the oscillation of a point is transverse to the wave propagation direction.

→ Now we will consider longitudinal waves, where the oscillation of a point is parallel to the wave propagation direction (sound travels this way).

Transverse Waves (reminder-this is what we did before)→ wave exists all along the string but we are considering

only a segment ∆x→ ∆x has a transverse displacement y

Longitudinal Waves: consider a rod

→ wave exists all through the rod but we just consider a small segment ∆x

→ in the presence of the wave our segment ∆x shifts and stretches by a longitudinal displacement ∆η

x

∆x

∆x + ∆η

Before Wave

In presence of wave

θ+∆θ

x x+∆x x

y

T

Tsegment of string

θ

SeeMath&physics demos website

Recall we summed forces on ∆x in the transverse (vertical) direction

For this case we must sum forces on ∆x in the longitudinal (horizontal) direction

4

The Wave Equation for Longitudinal Waves in a Rod(develop using similar procedure to stretched strings)

→ Strike the end of a rod you create a strain disturbance which moves along the rod

→ Our slice is shifted (due to cumulative strains) and also stretched by ∆η

→ experiences forces: F1 (at front of slice) F2 (at back of slice)

→ ∴ average strain across slice

→ ∴ average stress across slice

(assuming stress is in the longitudinal direction)

x∆∆= η

τη =∆∆=

xY

x∆x

x

x

∆x + ∆η

F1 F2

cross section α

Undisturbed

In the presence of the wave

thin slice

(exaggeratedscale and at some snapshot in time)

Why? section ∆x is stretched: so F1 and F2 depend on the interatomic separation at front and back of the slice. In string derivation we had different forces at each end of our segment also

Young’s modulus

5

→ To begin our wave equation determination, we need to sum the forces on our slice (like we did for the string earlier). Here we first look at stresses, then calculate the forces from the stresses. (note η is just the longitudinal displacement or stretch)

→ stress at point x:

→ stress at point x + ∆x

(strain at any point x)

xY

∂∂= η (partial derivative because here

strain is also time dependent)stress at x

how stress changes acrossany piece ∂x

( ) xx

stress ∆∂

∂+

xx

Yxx

Y ∆⎟⎠⎞

⎜⎝⎛

∂∂

∂∂+

∂∂= ηη

stress at x + ∆x = (stress at x)

xx

Yx

Y ∆∂∂+

∂∂= 2

2ηηstress at x + ∆x

6

Now we have the stresses at each end, lets get the forces…

xY

∂∂= ηα

xx

Yx

Y ∆∂∂+

∂∂= 2

2ηαηα

F = (cross sectional area)(stress)

∴ F1 = force at x α = cross sectional area

F2 = force at x+∆x

xx

YFF ∆∂∂=− 2

2

12ηα∑F

+gives

maFF =− 12

xm ∆= ρα 2

2

ta

∂∂= η

(on our slice)also

( ) ⎟⎟⎠

⎞⎜⎜⎝

⎛∂∂∆=∆

∂∂

2

2

2

2

txx

xY ηραηαbecomes

note

2

2

2

2

tYx ∂∂=

∂∂ ηρη WAVE EQUATION

for longitudinal waves!

cancelling terms gives

Note that η is just the longitudinal displacement, just like y was the transverse displacement for transverse waves

ρYv =

2

2

22

2 1tvx ∂

∂=∂∂ ηηor, if

another equation for wave velocity

7

Normal Mode Solutions to Longitudinal Wave Equation (similar to transverse - earlier)

→ Normal Mode Solution is of the type

→ evaluate f(x)

→ Boundary Conditions: for the string we had both ends clamped. This time we will only clamp one end (we could clamp the other end but we won’t – just to be different than last time).

BC #1: fixed end f(x)=0 at x=0 BC #2: free end ??? at x=L

→ Using BC #1 - same as for transverse waves on a string

→ What about BC #2? (this will tell us what ωn can be)→ At x=L we have a free end. This implies zero stress at this

point.

( ) ( ) txftx ωη cos, =

( ) ⎟⎠⎞

⎜⎝⎛=

vxAxf ωsin

Lxx

==∂∂ at 0η

1

2

(put back into wave eqn, same soln as for transverse p.134)

( )vxB

vxAxf ωω cossin +=

Lxx

F ==∂∂= at 0Y ηα

cross sectional area

τ

so

Note: this is the case because there are no stresses in any other directions to give us Poisson’s ratio effects

i.e. the very last row of atoms

8

→ To use this boundary condition we need to differentiate eqnbut lets put equation in first

12

( ) tvxAtx ωωη cossin, ⎟⎠⎞

⎜⎝⎛=

tvx

vA

xωωωη coscos ⎟

⎠⎞

⎜⎝⎛=

∂∂

Lxx

==∂∂ at 0η t

vL

vA ωωω coscos0 ⎟

⎠⎞

⎜⎝⎛=

⋅⋅⋅⋅⋅⋅=∴ ,2

5,2

3,2

πππω must vL

1 2+

differentiate wrt x

apply BC #2

0=∂∂

xηmust = 0 in order to have always

( ) ⋅⋅⋅⋅⋅⋅=−= ,2 ,1 with 21 nn

vL πω

or

( )L

vnn

πω 2

1−=

( )ρ

πω YL

nn

21−=

ρYv =

or with

These are the NM frequencies for a bar with one clamped andone free end, but also same for air channels with one end open

ρπω YL21 =

1ωω Cn = ( )⎥⎦

⎤⎢⎣

⎡=−

ρπ

ρπ Y

LCY

Ln

221

)21(2 −= nC 12 −= n

( ) 112 ωω −= nn

relationship betweenωn and ω1when one end free

soω2 = 3ω1ω3 = 5ω1ω4 = 7ω1

For n=1

9

Finally, we can write ωn in terms of fn(divide by 2π)

( )ρY

Lnfn 2

21−= ( ) 112 fnfn −=or

in Hz

Wave Equations and FunctionsSummarized

2

2

22

2 1ty

vxy

∂∂=

∂∂

2

2

22

2 1tvx ∂

∂=∂∂ ηη

µTv =

ρYv =

Transverse Waves (eg. stretched string)

Longitudinal Waves (eg. vibrating rod)

wave speed

normal mode solutions (standing waves)

normal mode solutions (standing waves)

( ) ( ) txftx ωη cos, =( ) ( ) txftxy ωcos, = general solution

one end fixed one end free

Boundary Conditions:

both ends fixed Boundary Conditions:

( ) tvxAtx n

nn ωωη cossin, =( ) t

vxAtxy n

nn ωω cossin, =

10

121

ωµ

πω nTL

nn =⎟

⎠

⎞⎜⎝

⎛=( ) ( ) 1

21

21

12 ωρ

πω −=⎟⎟⎠

⎞⎜⎜⎝

⎛−= nYL

nn

where

Also (in Hz)

21

22 ⎟⎟⎠

⎞⎜⎜⎝

⎛==

µπω T

Lnfn

( ) 21

21

2 ⎟⎟⎠

⎞⎜⎜⎝

⎛−=ρY

Lnfn

11

A Comparison of These 2 Waves(note these equations are only for specific boundary

conditions)

21

2 ⎟⎟⎠

⎞⎜⎜⎝

⎛=

µT

Lnfn

21

21

2 ⎟⎟⎠

⎞⎜⎜⎝

⎛−=ρY

Lnfn

Transverse 2 fixed ends

Longitudinal one end fixed

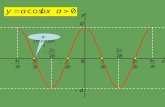
This implies that the string can accommodate an integral number of half sine curves

This implies that the length accommodates an integral number of quarter sine curves

n=1

n=2

n=1

n=2

n=3

one half-sin curve

two half-sin curves

one quarter-sin curve

three quarter-sin curves

five quarter-sin curves

(note: the above is really a longitudinal wave but I have represented it as a transverse one) - see website for longitudinal wave demos

At a snapshop in time the different harmonics look like:

This is actually 1/λ - convince yourself of this

12

The Wave Equation Revisited

→ General Wave Equation (1D):

Can write this for all sorts of situations!

→ stretched string(transverse oscillations):

→ longitudinal waves*in a solid:

→ transverse (shear)waves in a solid:

→ longitudinal wavesin a gas or liquid:

→ *Note: for longitudinal waves in a solid the elastic constant is “Y” only for a thin rod. When the transverse dimension is large then the correct modulus is for a constrained situation (see constrained modulus earlier).

2

22

2

2

xyv

ty

∂∂=

∂∂

where v is the wave speed

2

2

2

2

xyT

ty

∂∂=

∂∂

µ

2

2

2

2

xY

t ∂∂=

∂∂ η

ρη

µTv =

ρYv =

transverse displacement

tensionmass/ length

Young’s modulusdensity

longitudinal displacement

ρnv =

shear modulus

2

2

2

2

xyn

ty

∂∂=

∂∂

ρ

ρBv =

bulk modulus

2

2

2

2

xB

t ∂∂=

∂∂ η

ρη

13

Normal Mode in 2D and 3D Systems (French pg 181-189)

1D System: BCs at ends determine NM characteristics2D System: BCs at edges determine NM characteristics3D System: BCs at surfaces determine NM characteristics2D and 3D are an extension of 1D!For transverse wave - fixed both end (or all 4 edges for 2D)

2

2

2

2

ty

Txy

∂∂=

∂∂ µ

2

2

2

2

2

2

tz

syz

xz

∂∂=

∂∂+

∂∂ σ

( ) tLxnAtxy nnn ωπ cossin, ⎟⎠⎞

⎜⎝⎛=

( )tyxz nn ,,21

21

⎟⎠

⎞⎜⎝

⎛=µ

πω TL

nn

21

22

212

1

21 ⎥⎥⎦

⎤

⎢⎢⎣

⎡

⎟⎟⎠

⎞⎜⎜⎝

⎛+⎟⎟

⎠

⎞⎜⎜⎝

⎛⎟⎠⎞

⎜⎝⎛=

yxnn L

nLns ππ

σω

tL

ynL

xnC nnyx

nn 2121cossinsin 21 ωππ⎟⎟⎠

⎞⎜⎜⎝

⎛⎟⎟⎠

⎞⎜⎜⎝

⎛=

wave equation:

normal mode frequencies:

normal mode solution:

1D 2D

(nodes [zero amplitude] are points) (nodes are lines)

µ = linear densityT = tension

s = surface tensionσ = mass/unit areaLx, Ly = side lengths of membranen1, n2 are 1, 2, 3...

2

2

22

2

2

2

2

2 1tvzyx ∂Ψ∂=

∂Ψ∂+

∂Ψ∂+

∂Ψ∂

ρBv =

3D wave equation:

eg. in a gas - ψ might be a pressure magnitude at any given position and time