Position, Velocity, and Acceleration · Conclusion zThe velocity function is found by taking the...
Transcript of Position, Velocity, and Acceleration · Conclusion zThe velocity function is found by taking the...

Position, Velocity, and Position, Velocity, and AccelerationAcceleration
Mr. MiehlMr. Miehlwww.tesd.net/miehlwww.tesd.net/[email protected]@tesd.net

Position, Velocity & AccelerationPosition, Velocity & Acceleration
Velocity is the rate of change of positionwith respect to time.
Acceleration is the rate of change of velocitywith respect to time.
DVelocityT
Δ=Δ
VAccelerationT
Δ=Δ

Position, Velocity & AccelerationPosition, Velocity & Acceleration
When you’re driving your car…
Warning: Professional driver, do not attempt!

Position, Velocity & AccelerationPosition, Velocity & Acceleration
squeeeeek!
…and you jam on the brakes…

Position, Velocity & AccelerationPosition, Velocity & Acceleration
…and you feel the car slowing down…

Position, Velocity & AccelerationPosition, Velocity & Acceleration
…what you are really feeling…

Position, Velocity & AccelerationPosition, Velocity & Acceleration
…is actually acceleration.

Position, Velocity & AccelerationPosition, Velocity & Acceleration
I felt that acceleration.

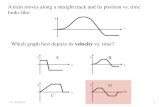
Position, Velocity & AccelerationPosition, Velocity & AccelerationHow do you find a function that describes a physical event?
Steps for Modeling Physical Data
1) Perform an experiment.
2) Collect and graph data.
3) Decide what type of curve fits the data.
4) Use statistics to determine the equation of the curve.

Position, Velocity & AccelerationPosition, Velocity & AccelerationA crab is crawling along the edge of your desk. Its location (in feet) at time t (in seconds) is given byP (t ) = t 2 + t.
a) Where is the crab after 2 seconds?
b) How fast is it moving at that instant (2 seconds)?

Position, Velocity & AccelerationPosition, Velocity & AccelerationA crab is crawling along the edge of your desk. Its location (in feet) at time t (in seconds) is given byP (t ) = t 2 + t.
a) Where is the crab after 2 seconds?
( ) ( ) ( )22 2 2P = +
( )2 6P = feet

Position, Velocity & AccelerationPosition, Velocity & AccelerationA crab is crawling along the edge of your desk. Its location (in feet) at time t (in seconds) is given byP (t ) = t 2 + t.
( ) 2= +P t t t
( ) ( )'= =V t P t
feet per second
b) How fast is it moving at that instant (2 seconds)?
2 1+t
( ) ( )' 2 2 2 1= +P
( )' 2 5=P
Velocity function
Velocity is the rate of change of position.

Position, Velocity & AccelerationPosition, Velocity & Acceleration
A disgruntled calculus student
hurls his calculus book in the air.

Position, Velocity & AccelerationPosition, Velocity & AccelerationThe position of the calculus book:
( ) 216 96p t t t= − +t is in seconds and p(t) is in feet
a) What is the maximum height attained by the book?
b) At what time does the book hit the ground?
c) How fast is the book moving when it hits the ground?

Position, Velocity & AccelerationPosition, Velocity & Accelerationa) What is the maximum height attained by the book?
( ) 216 96p t t t= − +
( )v t = ( )p t′ = 32 96t− +
Velocity function
0 32 96t= − +32 96t =
3t = seconds
( ) ( ) ( )23 16 3 96 3p = − +
( )3 144 288p = − +
( )3 144p = feet
The book attains its maximum height when its velocity is 0.

Position, Velocity & AccelerationPosition, Velocity & Accelerationb) At what time does the book hit the ground?
The book hits the ground when its position is 0.
( ) 216 96p t t t= − +20 16 96t t= − +
0 16 ( 6)t t= − −
16 0t− = 6 0t − =0t = 6t =sec. sec.

Position, Velocity & AccelerationPosition, Velocity & Accelerationc) How fast is the book moving when it hits the ground?
Good guess: 0 ft/sec This is incorrect.
( ) 32 96v t t= − +
( ) ( )6 32 6 96v = − +
( )6 192 96v = − +
( )6 96v = − ft/sec
Downward direction

Position, Velocity & AccelerationPosition, Velocity & Accelerationthe rate of change of velocity with respect to time.
Acceleration:
( ) 32 96v t t= − +
( ) ( ) 32a t v t′= = − ft/sec2
How is the acceleration function related to the position function?
Velocity function
Acceleration function
Acceleration is the second derivative of position.
( ) ( )a t p t′′=
Jerk is the rate of change of acceleration with respect to time.

Position, Velocity & AccelerationPosition, Velocity & AccelerationA red sports car is traveling, and its position P (in miles) at time t (in hours) is given by P (t ) = t 2 – 7t.
a) When is the car 30 miles from where it started?
b) What is the velocity at the very moment the car is 30 miles away?
d) When does the car stop?
c) What is the acceleration at the very moment the car is 30 miles away?

Position, Velocity & AccelerationPosition, Velocity & AccelerationA red sports car is traveling, and its position P (in miles) at time t (in hours) is given by P (t ) = t 2 – 7t.
a) When is the car 30 miles from where it started?
230 7= −t t
20 7 30= − −t t
( )( )0 10 3= − +t t
10 0− =t 3 0+ =t
10=t 3= −thours

Position, Velocity & AccelerationPosition, Velocity & AccelerationA red sports car is traveling, and its position P (in miles) at time t (in hours) is given by P (t ) = t 2 – 7t.
b) What is the velocity at the very moment the car is 30 miles away?
( ) ( )' 2 7= = −V t P t t
( ) ( )' 2 7= = −V t P t t
( ) ( )' 10 2 10 7= −P
( )' 10 13=P Miles per hour

Position, Velocity & AccelerationPosition, Velocity & AccelerationA red sports car is traveling, and its position P (in miles) at time t (in hours) is given by P (t ) = t 2 – 7t.
c) What is the acceleration at the very moment the car is 30 miles away?
( ) ( )' 2 7= = −V t P t t
( ) ( )'' 2= =A t P t Miles per hour2

Position, Velocity & AccelerationPosition, Velocity & AccelerationA red sports car is traveling, and its position P (in miles) at time t (in hours) is given by P (t ) = t 2 – 7t.
d) When does the car stop?
( ) ( )' 2 7= = −V t P t t
0 2 7= −t
7 2= t
3.5=t hours

ConclusionConclusionThe velocity function is found by taking the derivative The velocity function is found by taking the derivative of the of the positionposition function.function.
In order for an object traveling upward to obtain In order for an object traveling upward to obtain maximum position, its instantaneous velocity must maximum position, its instantaneous velocity must equal equal 00..
As an object hits the ground, its velocity is not 0, its As an object hits the ground, its velocity is not 0, its heightheight is 0.is 0.
The acceleration function is found by taking the The acceleration function is found by taking the derivative of the derivative of the velocityvelocity function.function.













![Local function vs. local closure function · Local function vs. local closure function ... Let ˝be a topology on X. Then Cl (A) ... [Kuratowski 1933]. Local closure function](https://static.fdocument.org/doc/165x107/5afec8997f8b9a256b8d8ccd/local-function-vs-local-closure-function-vs-local-closure-function-let-be.jpg)



