PHY 184 HW: Damped Oscillations homework problem
Transcript of PHY 184 HW: Damped Oscillations homework problem
Chapter 30 3
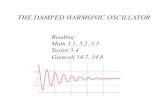
Read quantities of the graph ! The curve gives you two important pieces of information: The period and the amplitude of the sine wave. • Use the period to determine the angular frequency ω. • Use the decay of the amplitude to determine the exponential and
from that find the resistance R=RL. ! The sine wave peaks at t0 = 0 ms and at t1 = 0.7 ms
• ms = milliseconds, 10-3 s • This corresponds to 8 periods • Period T = 0.7 ms / 8 = 0.0000875 s • Thus the angular frequency is ω = 2π/T = 71808 Hz
! The peak at t1 has a height of V1 = 50 V ! Your graph may have a different voltage and period
Read voltage off the graph ! From the graph:
• V0 = 70 V • V1 = 50 V at t1 = 0.0007 s
! Voltage in a damped oscillating circuit:
! And each time the wave peaks, cos(ωt)=1, thus
! Here: R = 57.6 Ohm and R/2L = 480.8 s-1
Chapter 30 4
V =V0e− Rt
2L cos ωt( )
V1 =V0e
−Rt12L , hence R =
−2L ln V1 V0( )t1
Determine the capacitance ! From the frequency ω, determine first the resonance
frequency ω0
! And then determine the capacitance as
! ω0 = 71810 Hz, very close to ω because the exponential decay is gradual
! Thus C = 3.24*10-9 F = 3.24 nF
Chapter 30 5
ω = ω0
2 − R2L
⎛⎝⎜
⎞⎠⎟
2
thus ω0 = ω 2 + R2L
⎛⎝⎜
⎞⎠⎟
2
ω0 =
1LC
thus C = 1Lω0
2
Chapter 30 6
Determine the initial energy ! The initial energy in the capacitor is given by
! This is also the total initial energy in the circuit. Each time the voltage in the graph is at a maximum, the energy in the capacitor is at a maximum.
! This capacitor energy decays according to
! The cos2 term is =1 because we only consider the points in time where all the energy is in the capacitor
U0 =
12
CV 2 = 7.94×10−6 J
UE (t)=U0e−Rt
L
Question 1 ! Calculate the energy in the circuit after a time of 12 periods.
Note that the curve passes through a grid intersection point. ! After 12 periods, t12 = 0.00105 s and
! Thus the answer to the first question is 2.89E-6 J ! This makes sense: It is roughly 1/3 of the initial energy,
which would correspond to about 60% of the original voltage, which makes sense from the graph.
! You will likely read off different values from your graph and will have a different inductance. But you should be able to follow the steps in here.
Chapter 30 7
UE (t)=U0e−Rt
L = 7.94×10−6e−961.6∗t12 J = 2.89×10−6 J
Question 2 ! Calculate the time required for 93% of the initial energy to
be dissipated. ! In order for 93% of the initial energy to be dissipated, we
need 7% of the initial energy remaining, or
! Thus
! This makes sense, it is a bit longer longer than t12
Chapter 30 8
U93(t93 )=U0e−Rt93
L where U93 = (1−0.93)U0
0.07 = e
−Rt93L and t93 = −
LR
ln0.07 = 0.00277s
Conclusions ! This is a complicated problem involving many steps ! You should know how to read numbers off the graph
• Period, and converting it to ω • You should be able to compute the capacitance C • Voltage and its time dependence • You should be able to compute R
! You should understand how to calculate the initial energy U0
Chapter 30 9