Momentum of Inertia of some symmetric bodies

Rotational kinetic energy

KROT =

=

It is called MOMENTUM of INERTIA

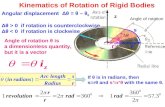
Rotation around a fixed axis

ω M

( )

Momentum of Inertia of some rigid bodies

DISK of radius R and Mass M

DISK of radius R and Mass M

Parallel axis theorem

CMM

I = ICM + M h2

X

YCM

yi

xiRi

a

a

Work and Kinetic Energy

ΔK = W

z

E = K + mg z Mechanical energy is conserved

E = m vCM2 + I ω2 + mg z

E is conserved throughout the motion

In particular , if the system of particles moves under the action of a conservative force, like the gravitational force for example, we obtain

Kf + mg zf = Ki + mg zi

m

APPENDIX Conservation of the Mechanical Energy Rigid Body Motion

While the ball is rolling down, what is the work done by all these 4 types of forces?

Internal forces

Instantaneous point of contact

m1m2m3

Ftotal = N + Ff +

Ff

N : It acts on a different mi each time. It acts on the so called "point of contact." The only possible displacement of the point of contact would be perpendiculat to N. Therefore, the work done by N is zero.

N

N i

g

Rigid body

Ff : It acts on the rolling ball through the instantaneous point of contact (ipc). If we assume no slipping, the instantaneous velocity of the ipc is zero. Therefore, there will not be kinetic friction; i.e. Ff does not do work. There is static friction, but such a force does not produce work

Fij Let's evaluate the work done by the internal forces. Consider two arbitrary small masses mi and mj. There will be a couple of action and reaction forces Fij and Fji acting on these two particles. Let's calculate the work done by this couple of internal forces

ij

g

mi

mj

The

=

=

+ +

Since we are dealing with a rigid body, the magnitude of the vector ( ri - rj ) remains constant throughout the motion.

)

Then, the only possible orientation of d(ri - rj ) is to be perpendicular to the line that passes through mi and mj .

)

Therefore,

= 0

d(ri - rj ) ( ri - rj )

d(ri - rj ) Fij

) )

)

- mi g ( zfinal, i - zinitial, i )

regardless of the tra-

zfinal, i

If we extend this argument to all pairs of particles of the rigid body we conclude: The work done by the internal forces in a rigid body is zero

Thus, the only force that produces work on the rolling block is the gravitational force

We already know that regardless of the trajectory followed by the "small" particle mi the work done by the gravitational force is,

As the block rolls down, a particular "small" mass mi undergoes a complicated trajectory.

zinitial, i

mi gzfinal, i mi gzinitial, i )(

Adding up all the work done on each particle, one obtains

-(

W =

W = M g zCM, final - M g zCM, initial )

zCM, final

zCM, initial

Z

H = 2m

vi=0

vf= ?

zCM

1

1

Practice problem A 1 m long rod of mass m = 0.2 Kg is hinged at one end and

connected to a wall. It is held out horizontally , then released. With respect to the reference XY, whose origin is at the hinge (as shown in the figure), calculate:

The speed of the tip of the rod at the moment it hits the wall? The kinetic energy of the rod at the moment it hits the wall?

vtip

X

Y

L= 1 m

Wall

2

1

A thin uniform rod of length L = 2.0 m and can pivot about a horizontal, frictionless pin through one end. It is released from rest at angle q = 40o above the horizontal. Use the principle of conservation of mechanical energy to determine the angular speed of the rod as it passes through the horizontal position.

40o

Solution

40o