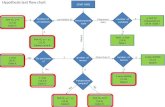
Hypothesis test flow chart
description
Transcript of Hypothesis test flow chart

40 50 60 70 80 90 100Frequency
0
10
20
30Exam 1, mean: 85.1, median: 90.0
40 50 60 70 80 90 100Frequency
0
10
20
30
40Exam 2, mean: 85.5, median: 91.0

40 50 60 70 80 90 100Exam 1, mean: 85.1, median: 90.0
40
50
60
70
80
90
100
Exa
m 2
, mea
n: 8
5.5,
med
ian:
91.
0
r = 0.46

Chapter 13: Interpreting the Results of Hypothesis Testing
‘statistically significant’ does not mean ‘important’
IQ’s of UW undergraduatesSuppose we measured the IQ’s of 10,000 UW undergraduates and found a mean IQ of 100.3. If we were to conduct a one-tailed z-test to determine if this mean is greater than the US population that has a mean of 100 and a standard deviation of 15. Use a = .05
215.1003.100
X
X
suXz
-3 -2 -1 0 1 2 3z
15.1000015
nss X
X
We’d find that we could reject H0 with a=.05.
But is a difference of 0.3 IQ points important?
area = a = .05
z=2

If you want to read a lot about statistically significant effects that have small effect sizes…

Some journals require the authors to report the ‘effect size’, along with the outcomes of statistical tests to let the reader interpret whether the effect is ‘big’ enough to be important.
Remember, to calculate t, we divide by the standard error of the mean:
But the standard error of the mean shrinks with increasing n.
We need a measure of the size of the difference between our observation and the null hypothesis that doesn’t depend on experimental parameters like n.
X
hyp
suX
t

One example of effect size is Cohen’s d:
Where mhyp is the mean for the null hypothesis. This is just like converting the sample mean to a z score.
A more common example is Hedge’s g, which is used when we don’t know the standard deviation of the population. It’s our best estimate of Cohen’s d:
This is just like calculating a value for the t-distribution except we divide by sX
instead of the standard error of the mean
Effect size: the difference between our observation and the null hypothesis in terms of standard deviations. Formally: effect size is “an estimate of the degree to which the treatment effect is present in the population, expressed as a number free of the original measurement unit”.
X
hyp
suX
g
X
hypuXd

Back to our made-up IQ example where we had a mean of 100.3 and a standard deviation of 15
The effect size is:
The study found that UW IQ’s are only 0.02 standard deviations above 100.
This is a small effect size, even though it is statistically significant.
02.151003.100
X
hypuXd

Reporting effect size has the advantage that since it doesn’t depend on n, the value is more easily compared across studies.
A conventional interpretation of effect size is that (in absolute value):
0.8 is large,0.5 is medium
0.2 is small.
0.80.5 0.2

There are two unavoidable types of errors in hypothesis testing: type I and type II errors.
A Type I error is when we reject H0 when it is actually true. Pr(Type I error) = a
A Type II error is when we fail to reject H0 even though it false. Pr(Type II error) = b
More commonly, we talk about the probability of correctly rejecting H0, The probability of this happening is called power:
Power = Pr(correct rejection of HO) = 1-b.
True state of the worldDe
cisio
n ba
sed
on y
our s
ampl
e
Type I Error (a)
Type II Error (b)
Correctly reject H0 (1-b = power)
Correctly fail to reject HO (1-a)Fail to reject HO
Reject HO
HO is true HO is false

-3 -2 -1 0 1 2 3 4 5 6 7
-3 -2 -1 0 1 2 3 4 5 6 7
-3 -2 -1 0 1 2 3 4 5 6 7
-3 -2 -1 0 1 2 3 4 5 6 7
HO is true HO is false
True state of the worldDe
cisi
on b
ased
on
you
r sam
ple
Fail
to re
ject
HO
Reje
ct H
O
Correctly fail to reject HO (1-a)
Type II Error (b)
Type I Error (a)
Correctly reject H0 (1-b = power)

Alpha (a) is therefore the probability that a Type I error will occur.
Type I errors (a)
A Type I error occurs when our statistic (z or t) falls within the region or rejection even though the null hypothesis is true.
For example, for a one-tailed z-test using a = .05, the distribution of z scores and the rejection regions look like this:
-4 -3 -2 -1 0 1 2 3 4z score
Pr(Type I error) = a

At Type II error happens when the null hypothesis is false but you fail to reject it anyway.
To calculate the probability of a type II error, we need to know the true distribution of the population.
This is weird because the true distribution of the population is the thing we’re trying to figure out in the first place.
Type II errors

Type II errors happen only if the null hypothesis is false.For example, suppose we’re conducting a one-tailed z-test with a = .05, and the true population mean has a mean z score of 1 (mtrue = 1). We still use the same critical value that we did under the null hypothesis. But now the distribution of z-values is centered around z=1.
The blue shaded region is the probability of correctly rejecting the null hypothesis. Type II errors happen when z falls outside the rejection region, so the probability of making a Type II error is 1- blue shaded area.
Type II errors: beta (b) and power (1-b)
mhyp = 0
mtrue = 1 Zcrit = 1.645
-3 -2 -1 0 1 2 3 4 5
1b = power (blue shaded area)
z-score
a Pr(type I error) (red shaded area)

Calculating power, the probability of correctly rejecting HO
1) Find the rejection region under the null hypothesis:With a = .05, zcrit = 1.645 (Table A, column C), so the rejection region is z>1.645
2) The new rejection region will by shifted down by utrue – uhyp = 11.645-1 = 0.645, so the new rejection region is z>0.645
3) Find the area in the new rejection regionThe power is the area for z above 0.645 is .2611 (Table A, Column C)
Type II errors: beta (b)
mhyp = 0
mtrue = 1 Zcrit = 1.645
-3 -2 -1 0 1 2 3 4 5
1-b = power (blue shaded area)
z-score
a (red shaded area)

power = 1-b
Power is the probability of correctly rejecting the null hypothesis, which is the area in the rejection region.
Power in this example is: Pr(z>0.645) = 1-b = .2611 More power is good. Power is the probability of correctly finding an effect in your experiment.
A ‘desirable’ level of power is .8
mhyp = 0
mtrue = 1 Zcrit = 1.645
-3 -2 -1 0 1 2 3 4 5
1-b = power (blue shaded area)
z-score
a (red shaded area)

Example: IQs are normally distributed with a mean of 100 and a standard deviation of 15. Suppose you sampled 100 students and calculated a sample mean and are about to test for a significant increase in IQ using a one-tailed z-test using a=.05. What is the power of this test under the assumption that the true population mean for the group that we’re sampling is 103?
Answer: First, we’ll convert everything to z-scores. This makes mhyp = 0 (always), and
25.11001035.1
10015
trueX nm

-4 -3 -2 -1 0 1 2 3 4z-score
25.11001035.1
10015
trueX nm
To calculate power:
1) Find the critical value of t under null hypothesis:With a = .05, zcrit = 1.64 (Table A, column C), so the rejection region is z > 1.64
2) The new rejection region will by shifted over by utrue – uhyp = 2-0 = 2z > 1.64-2, which is z `> -.36
3) Find 1-b, the area in the new rejection regionPr(z > -.36) = .6406
A power of .6406 means that there is a 64.06% chance of correctly rejecting the null hypothesis (or not making a type II error).
power = 1-b = .6406

Things that affect power: Variability of the measure
Power increases as the standard error of the mean decreases.
-3 -2 -1 0 1 2 3 4 5z score
power =0.2595
-3 -2 -1 0 1 2 3 4 5z score
power =0.6388
-3 -2 -1 0 1 2 3 4 5z score
power =0.9907
-3 -2 -1 0 1 2 3 4 5z score
power =0.3777
Ways to decrease the standard error of the mean:1) Increase the sample size (increase n)2) Make more accurate measurements (decrease )nX
1X75.0X
5.0X 25.0X
a=.05 mtrue = 1.0 ?X

Things that affect power: level of significance (a)
-3 -2 -1 0 1 2 3 4 5z score
power =0.0183
-3 -2 -1 0 1 2 3 4 5z score
power =0.1685
-3 -2 -1 0 1 2 3 4 5z score
power =0.2595
-3 -2 -1 0 1 2 3 4 5z score
power =0.0924
a=.05 a=.025
a=.01 a=.001
a=? mtrue = 1.0 1X
Power decreases as alpha (a) decreases.
This is a classic tradeoff: The less willing we are to make a Type I error, the more likely we are going to make a Type II error.

-3 -2 -1 0 1 2 3 4 5z score
power =0.0815
-3 -2 -1 0 1 2 3 4 5z score
power =0.2595
-3 -2 -1 0 1 2 3 4 5z score
power =0.1261
-3 -2 -1 0 1 2 3 4 5 6 7 8z score
power =0.9907
Things that affect power: difference between utrue and uhyp
Power increases with effect size: as the difference between means for the true population and the null hypothesis increases.
mtrue = 0.25 mtrue = 0.5
mtrue = 1.0mtrue = 4.0
We don’t have control over this: mtrue is the one thing we don’t know (but want to estimate).
a=.05 mtrue = ? 1X

0 0.2 0.4 0.6 0.8 10
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Effect size (d)
Pow
er
Sample size = 50
Power curve: shows how power increases with effect sizeTwo-tail a=.05

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1 1.2 1.3 1.40
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
n=8
1012
15
20
2530
4050
75
100
150
250
500
1000
Effect size (d)
Pow
er
a = 0.01, 1-tail, 1 mean

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1 1.2 1.3 1.40
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
n=810
1215
2025
30
4050
75100
150
250
5001000
Effect size (d)
Pow
er
a = 0.05, 1-tail, 1 mean

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1 1.2 1.3 1.40
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
n=8
10
12
15
20
25
30
40
50
75
100
150
250
500
1000
Effect size (d)
Pow
er
a = 0.01, 2-tails, 1 mean

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1 1.2 1.3 1.40
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
n=8
1012
15
20
2530
4050
75
100
150
250
500
1000
Effect size (d)
Pow
er
a = 0.05, 2-tails, 1 mean

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1 1.2 1.3 1.40
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
n=8
1012
15
20
2530
40
50
75
100
150
250
500
1000
Effect size (d)
Pow
er
a = 0.01, 1-tail, 2 means

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1 1.2 1.3 1.40
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
n=8
1012
15
20
2530
4050
75100
150
250
500
1000
Effect size (d)
Pow
er
a = 0.05, 1-tail, 2 means

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1 1.2 1.3 1.40
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
n=8
1012
15
20
25
30
40
50
75
100
150
250
500
1000
Effect size (d)
Pow
er
a = 0.01, 2-tails, 2 means

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1 1.2 1.3 1.40
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
n=8
1012
15
20
2530
40
50
75
100
150
250
500
1000
Effect size (d)
Pow
er
a = 0.05, 2-tails, 2 means

Example: Suppose we’re conducting a two-tailed t-test with one mean with a = .05 with a sample size of n=50. How much of an effect size do we need to obtain a power value of 0.8?
Answer: Looking at the appropriate family of power curves, the curve with n=50 passes through a power value of 0.8 when the effect size is 0.4.
Example: Suppose we’re conducting a one-tailed t-test with one mean with a = .01 and we have an effect size of 0.6. How large of a sample size do we need to get a power value of 0.8?
Answer: Looking at the appropriate family of power curves, looking at a power value of 0.4, the curve with n=30 passes through a power value of 0.8.

Example: You decide to sample the test scores of 63 dazzling cats from a population and obtain a mean test scores of 25.6 and a standard deviation of 2.77. Using an alpha value of α = 0.01, is this observed mean significantly different than an expected test scores of 25?
What is the effect size? What is the power?

Example: You decide to sample the test scores of 63 dazzling cats from a population and obtain a mean test scores of 25.6 and a standard deviation of 2.77. Using an alpha value of α = 0.01, is this observed mean significantly different than an expected test scores of 25?
What is the effect size? What is the power?
Answer: (Two tailed t-test for one mean) We fail to reject H0 (t(62) = 1.72, tcrit = ±2.6575). The test scores of dazzling cats is not significantly different than 25. Effect size: 0.2166 Power = 0.1759

Example: Suppose we’re conducting a two-tailed t-test with a = .05 with a sample size of n=50. How much of an effect size do we need to obtain a power value of 0.8?
Answer: Looking at the appropriate family of power curves, the curve with n=50 passes through a power value of 0.8 when the effect size is 0.4.
Example: Suppose we’re conducting a one-tailed t-test with a = .01 and we have an effect size of 0.6. How large of a sample size do we need to get a power value of 0.8?
Answer: Looking at the appropriate family of power curves, looking at a power value of 0.4, the curve with n=30 passes through a power value of 0.8.

Example: You decide to sample the test scores of 63 dazzling cats from a population and obtain a mean test scores of 25.6 and a standard deviation of 2.77. Using an alpha value of α = 0.01, is this observed mean significantly different than an expected test scores of 25?
What is the effect size? What is the power?

Example) You decide to sample the test scores of 63 dazzling cats from a population and obtain a mean test scores of 25.6 and a standard deviation of 2.77. Using an alpha value of α = 0.01, is this observed mean significantly different than an expected test scores of 25?
What is the effect size? What is the power?
Answer) (Two tailed t-test for one mean) We fail to reject H0 (t(62) = 1.72, tcrit = ±2.6575). The test scores of dazzling cats is not significantly different than 25. Effect size: 0.2166 Power = 0.1759