1

Simple Harmonic Motion 1-Theory

Simple harmonic motion refers to the periodic sinusoidal oscillation of an object or quantity. Simple harmonic motion is executed by any quantity obeying the Differential Equation

,020 =+ xx ω&& (1)

where, x&& denotes the second Derivative of x with respect to t , and 0ω is the angular frequency of oscillation. This Ordinary Differential Equation has an irregular Singularity at ,∞ . The general solution is

x = )cos()sin( 00 tBtA ωω + (2) = )cos( 0 φω +tC (3)

where the two constants A and B (or C andφ ) are determined from the initial conditions.

Many physical systems undergoing small displacements, including any objects obeying Hooke’s Law, exhibit simple harmonic motion. This equation arises, for example, in the analysis of the flow of current in an electronic CL circuit (which contains a capacitor and an inductor ). If a damping force such as Friction is present, an additional term x&β must be added to the Differential Equation and motion dies out over time.

Adding a damping force proportional to x& , the first derivative of x with respect to time, the equation of motion for damped simple harmonic motion is

,020 =++ xxx ωβ&&& (4)

where β is the damping constant. This equation arises, for example, in the analysis of the flow of current in an electronic CLR circuit, (which contains a capacitor, an inductor, and a resistor ). This Ordinary Differential Equation can be solved by looking for trial solutions of the form rtex = . Plugging this into (4) gives

0)( 20

2 =++ rterr ωβ (5)

020

2 =++ ωβ rr (6)

This is a Quadratic Equation with solutions

).4(21 2

02 ωββ −±−=r (7)

2

There are therefore three solution regimes depending on the Sign of the quantity inside the Square Root,

.4 20

2 ωβα −= (8)

The three regimes are 1. α > 0 is Positive: overdamped,

2. α = 0 is Zero: critically damped,

3. α < 0 is Negative: underdamped.

Under-damped simple harmonic motion occurs when

3

04 20

2 <− ωβ (9)

so 04 2

02 <−≡ ωβα (10)

Define

,421 22

0 βωαω −=−≡ (11)

then the solutions satisfy

γβ ir ±−=± 21 , (12)

where

−±−≡±

20

2 421

ωββr , (13)

and are of the form tiex )2/( γβ ±−= (14)

Using the Euler Formula xixe ix sincos += (15) this can be rewritten:

[ ]).sin().cos()2/( titex t ωωβ ±= − (16) We are interested in the real solutions. Since we are dealing here with a linear homogeneous ODE, linear sums of linearly independent solutions are also solutions. Since we have a sum of such solutions in (64), it follows that the Imaginary and real part separately satisfy the ODE and are therefore the solutions we seek. The constant in front of the sine term is arbitrary, so we can identify the solutions as

1x = [ ]).cos()2/( te t ωβ− (17)

2x = [ ]).sin()2/( te t ωβ− (18) so the general solution is

[ ]).sin().cos()2/( tBtAex t ωωβ += − (19)

2- Experiment

4

2-1 Object: To study Hooke’s law, and simple harmonic motion of a mass oscillating on a spring. 2-2 Apparatus: Rotary motion sensor, thin string, uniform spring, balance, weight hanger and weight, computer Pasco Model 700 Interface, printer.

2-3 Procedure:

1- Adjust the apparatus. Setup the apparatus as shown in the figure. The 500 g weight on the right pan goes on the floor that the spring is attached to and on the other pan (that is on left) you put 40 g weight (about 40g positioned on the floor) so that the spring and the scale are vertical. Take that position of the pan as the equilibrium position.

2- Start the data collection – add extra mass m such as 10g, 20g, 30g and 40g to further stretch the spring. For each extra mass m, allow the pan to go down very slowly to the maximum position x and stop the data collection. Enlarge the position’s table –you can record the extra stretch x. Repeat this with the different weights. Plot mg vs. x, draw a straight line through the origin and all the points. (g is the gravity acceleration constant ). The slope of the line is the spring constant k

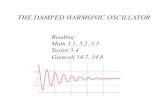
3- Remove the extra masses and come back to the equilibrium position (with 40g). Displace the whole weight by a small vertical distance (an inch or two). Release the system and start the collection data at the same time. When the oscillations (vibrations) vanish, stop the data collection. On the graph of the position vs. time, use the sine fit to fit all sinusoidal plots. You can read the period of oscillations and calculate the value of the

corresponding frequency 1ω . Now, using the formula 1

21 m

k=ω calculate the real

mass 1m .What is your conclusion?

5

4- Use the computer pencil to draw the line that connects the top peaks of the position’s waves.

5- Use the Natural Exponent fit to fit that line. The exponent C gives you the value of 2/β . Infer the value of the damping constant β .

6- Repeat the same experiment for the extra mass of 40 more grams. 7- Print all graphs and tables.