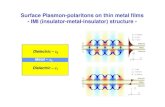
Plasmonics · Plasmonics Femius Koenderink Center for Nanophotonics AMOLF, Amsterdam Plasmon:...
Transcript of Plasmonics · Plasmonics Femius Koenderink Center for Nanophotonics AMOLF, Amsterdam Plasmon:...
-
1
Plasmonics
Femius Koenderink Center for Nanophotonics AMOLF, Amsterdam
Plasmon: elementary excitation of a plasma (gas of free charges) Plasmonics: nano-scale optics done with plasmons at metal interfaces
-
Flavours
M-I-M Taper and wire
Hybrid V-groove Wedge/hybrid
-
1) Kramers-Kronig bounds on ε
2) Back to the surface plasmon
3) Pulse propagation and dispersion
-
Kramers-Kronig
2013 /
4
Can a material have arbitrary real and imaginary ε ? No: material response functions are constrained by causality
Frequency domain
Time domain Note how convolution turns to product
Physics: no response before cause
-
Causal response
Example of an allowable response function in time What does Imply for
-
Even and odd / real, imaginary
Three important realizations: 1) χ(t) is a real function 2) It’s even part contributes to the real part of χ(ω) 3) It’s odd part contributes to the imaginary part of χ(ω)
-
So what is the even / odd part ?
Define as odd part of the response function This has no physical meaning, just a math trick
-
So what is the even / odd part ?
The even part of χ(t) follows from the odd part
So now: Fourier transform of a product is a convolution of FTs
-
So what is the even / odd part ?
So what is the Fourier transform of sgn(t) ? Remember
-
Kramers-Kronig
Therefore the imaginary part of the frequency-dependent Permittivity completely specifies the real part Similarly
-
Kramers Kronig
Either you have non-dispersive vacuum ε=1, i.e., χ=0, or - A window of real χ implies a window of absorption - Real χ(ω) >0 means χ(ω) < 0 at other ω (to avoid gain) - “No dispersion” but a refractive index not 1 is impossible
Considerations hold for any physical response function
-
Typical solids
Absorption bands close to intrinsic resonances Real n to the red also outside absorption Most materials have ’normal dispersion’, i.e.,
goes up with energy is higher towards the blue is higher towards short
Until you go through an absorption resonance
-
Phase velocity
A front of constant phase follows
Phase velocity
Suppose now I have a wave packet
e.g.
Note that at x=0, this is just a pulse
-
Group velocity
Maybe you have dispersion
The pulse envelope has a velocity
known as the group velocity
-
Dispersion relation in a gas
15
Near resonance (γ ~ 0.05 ω0) - Strongly dispersive - Very low vg - Superluminal phase velocity - Negative & superluminal vg
-
Indices
Group index very different from phase index Negative vg Superluminal vg, vf
Region of strong absorption – Kramers-Kronig in action
-
Movie – dispersive propagation
Strongly dispersive, weakly absorbing ωc~ 0.85 ω0 (here loss length > 50λ) Pulse envelope tracks vg
-
Strongly dispersive, weakly absorbing (here loss length > 50λ) Pulse envelope tracks vg
-
Superluminal phase
Strongly dispersive, strongly absorbing ωc~ 1.03 ω0 vf=1.25c, vgroup=1.7c (at carrier frequency) Note how the packet - barely moves - vg >c not apparent - package break up
Loss length ~ 3 λ
-
Slow light, superluminal phase
Superluminal phase Slow group velocity Weak abosrption ωc~ 1.1 ω0 vf=1.15c, vgroup=c/2 (at carrier frequency) Note how the group velocity has regained meaning Loss length ~ 20 λ
-
Take home messages
• Phase velocity describes phase front propagation You get it from the ratio of ω/c and |k|
• For weak absorption, group velocity describes Gaussian envelope • Strong dispersion also entails strong absorption • Superluminal phase and group velocities appear • These are irrelevant to describe pulse-energy propagation
• Pulse break up (group velocity dispersion) • Strong attenuation
Note: - this has been a big controversy in Nature/Science Plasmonics is strongly dispersive and at superluminality paradox
-
Small scatterers and plasmonics
-
23
From plasmon to plasmonics
Plasmons in the bulk oscillate at ωp determined by the free electron density and effective mass
Plasmons confined to surfaces that can interact with light to form propagating “surface plasmon polaritons (SPP)”
Confinement effects result in resonant SPP modes in nanoparticles
+ + +
- - -
+ - +
k
0
2
εω
mNedrude
p =
0
2
31
εω
mNedrude
particle =
2
0
12
drude
surfaceNem
-
Observables
Extinction cross section [m2] Power removed from beam Incident intensity
Extinction = scattering + absorption
removed from the beam
Re-radiated into all angles
Lost as heat in the scatterer
-
Physical quantity - polarizability
Small object kd
-
Electrostatic sphere
First consider a sphere in a static field
E0 εm ε
z
r
θ
a
( )( )ar
ar>=∆Φ
-
Solution
20203
02
0001
42
23
2
rp
rEr
EarE
rErErE
mm
m
m
m
m
m
πεθθθ
εεεε
θ
θεε
εθ
εεεε
θ
coscos
coscos
coscoscos
+−=
+−
+−=Φ
+
−=
+−
+−=Φ
E0 εm ε
z
r
θ
a Easy to verify
30 0 with 4 2
mSI SI m
m
p E a ε εα α πε εε ε
−= = +
Inside sphere: homogeneous field Outside sphere: background field plus field of a dipole with
In the ball:
Outside:
-
Metal sphere
Drude model for a metal: Lorentzian `plasmon resonance’
2 23 0
2 20
1 means ( )
peasy ai i
ω ωε αω ω γ ω ω ωγ
= − = + − +
• Resonance where ε(ω0) = -2 εm • Response scales with the volume V • α exceeds V by factor 5 to 10 • Shape shift condition ε = -2 εm
30 04 with 2
measy easy
m
p E a ε επε α αε ε
−= = +
-
Observables
Extinction cross section [m2] Power removed from beam Incident intensity
Extinction = scattering + absorption
removed from the beam
Re-radiated into all angles
Lost as heat in the scatterer
-
Revisiting polarizability Classical model of harmonically bound electron describes atom, and scatterer alike as an oscillating dipole
20 0
2 20
3 ( ) ( )i t i tSIVt e e
iω ωε ω α ω
ω ω ωγ= =
− −p E E
Lorentzian resonance
Extinction: how much power is taken from the beam ? Cycle average work done by E on p
in ImdpW Edt
α∝ ⋅ ∝
-
Revisiting polarizability Extinction: how much power is taken from the beam (in SI units) ?
0 0
1 1Re[ ] Re[ ] Re[ ] Re[ ]T Ti t
i t i t i td eW e dt e i e dtT dt T
ωω ω ωωα= ⋅ = ⋅∫ ∫
pE E E
* * *
0
1 ( ) ( )4
Ti t i t i t i tW e e i e i e dt
Tω ω ω ωωα ωα− −= + ⋅ −∫ E E E E
Only cross terms survive cycle average * 2 2
0
1 ( | | | | ) oscill.terms ( 2 )4
T
W i i dtT
ωα ωα ω= − + + ±∫ E E
2Im | |2
W ω α= E
-
Revisiting polarizability Classical model of harmonically bound electron Describes atom, and scatterer alike
Scattering: how much power does p radiate ?
22
0
2
0 0
22dipole
2
0 0
2 ||4
sinsin||sin W απε
θθϕθϕπ ππ π
∝=∝⋅∝ ∫ ∫∫ ∫∫ rprdErddA
sphere
nS
Lorentzian resonance
20 0
2 20
3 ( ) ( )i t i tSIVt e e
iω ωε ω α ω
ω ω ωγ= =
− −p E E
-
Equate extinction to scattering (energy conservation)
Scattering
Rayleigh / Larmor
Extinction
Work done to drive p
≥
Optical theorem
2 4 k Im [ ]Easy mπ α 4 2 28 k | | [ ]3 Easy
mπ α
1. Very small particles scatter like r6/λ4 (Rayleigh) 2. For very small particles absorption wins ~ r3/λ 3. Big |α|2 implies large Im α
-
Equate extinction to scattering (energy conservation)
Scattering
Rayleigh / Larmor
Extinction
Work done to drive p
≥
Optical theorem
2 4 k Im [ ]Easy mπ α 4 2 28 k | | [ ]3 Easy
mπ α
Since |Im α | < |α|
33| |2 2Easy
λαπ
<
Upper bound on the strongest possible dipole scatterer
-
Example: simple spheres
Calculated exact cross section of Au spheres r=10 -50 nm Dashed line: σ = 4π k Im αeasy Surprises -Peak bounded by
-
Revisiting polarizability Classical model of harmonically bound electron describes atom, and scatterer alike as an oscillating dipole
20 0
2 20
3 ( ) ( )i t i tSIVt e e
iω ωε ω α ω
ω ω ωγ= =
− −p E E
Lorentzian resonance
Compared to electrostatics: γ must be adapted to contain radiation damping
-
Summary • Small particles of size < λ/10 scatter like dipoles • Generally: 3x3 polarizability tensor proportional
to V • ‘Depolarization factors’ require microscopic
model • General features of polarizability
– Optical theorem contrains α – Polarizability bounded by above by unitary limit – Radiative damping broadens resonances & raises
albedo
-
Photochemical imaging
39
Plasmon particles in azo-polymer Regions of high field contract Measured using atomic force microscopy Wiederrecht
-
Uses of particle plasmons
40
Very strong local fields |E|2: 104 x stronger than incident
Au spheres 5,8,20 nm, gaps of 1-3 nm
100 102 104
|E|2/|Ein|2
10.000 times enhanced optical field intensity
-
Resonance shifts
Single protein binding & unbinding
-
Bow ties
Measured 1000 x fold enhancement of # photons / molecule
Wenger – Inst. Fresnel, Marseille
-
Example – dimer in static approximation
Dimer in a static approximation
Linear problem • Symmetric, but not real matrix • 1/polarizability on the diagonal • Interaction on the off-diagonal - this will shift resonances
-
Hybridization (exercise)
-
Plasmon ruler
Idea: Alivisatos group
-
Yagi Uda antenna
Curto et al., Science (2010).
-
Directional scattering, phased arrays
Arrays of particles can result in directional scattering Arrays of particles can result in directional emission When a local source is embedded
-
Yagi-Uda
Optical domain: a chain of plasmon particles driven by a single molecule
-
Phased array
Suppose I have N dipoles, radiating into the far field as
Taylor expand for large Viewing distance
r1 r2
-
Far field
Overall spherical wave
If all dipoles are parallel (not meaning in phase)
Array geometry ‘Structure factor’
Single scatterer ‘Form factor’
-
Uses of particle plasmonics
• Enhanced fields for spectroscopy • Sensing • Enhanced fluorescence brightness • Fluorescence directionality
Slide Number 1FlavoursSlide Number 3Kramers-KronigCausal responseEven and odd / real, imaginarySo what is the even / odd part ?So what is the even / odd part ?So what is the even / odd part ?Kramers-KronigKramers KronigTypical solidsSlide Number 13Slide Number 14Dispersion relation in a gasIndicesMovie – dispersive propagationSlide Number 18Superluminal phaseSlow light, superluminal phaseTake home messagesSlide Number 22From plasmon to plasmonicsObservablesPhysical quantity - polarizabilityElectrostatic sphereSolutionMetal sphereSlide Number 29ObservablesRevisiting polarizabilityRevisiting polarizabilityRevisiting polarizabilityOptical theoremOptical theoremExample: simple spheresRevisiting polarizabilitySummaryPhotochemical imagingUses of particle plasmonsResonance shiftsBow tiesExample – dimer in static approximationSlide Number 44Plasmon rulerYagi Uda antennaDirectional scattering, phased arraysYagi-UdaPhased arrayFar fieldUses of particle plasmonics