MCRT: L5• MCRT estimators for mean intensity, absorbed

radiation, radiation pressure, etc • Path length sampling: mean intensity, fluence rate,

number of absorptions • Random number generators

Mean Intensity

∫∫∫ =Ω=π

ν

π

νν φθθππ 0

2

0ddsin

41d

41 IIJ

Same units as In: J/m2/s/Hz/sr (ergs/cm2/s/Hz/sr)

Function of position (and time), but not direction

Determines heating, ionization, level populations, etc

dA

q

In(r, n)dW

s

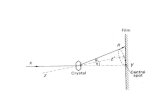
What is Jn at r from a star with uniform specific intensity I* across its surface?

R*

r

q*

I*

I = I* for 0 < q < q* (µ* < µ < 1); µ = cos qI = 0 for q > q* (µ < µ*)

J = 12

I dµ = 12 I*(1−µ*)µ*

1∫

J = I* 12 1− 1− R*2 / r2( ) = wI*

w = dilution factorLarge r, w = R2/4r2

Energy passing through a surface. Units: J/s/m2/HzFlux in the direction n from radiation passing through

dA at angle q is reduced because the foreshortened area is smaller:

dFn = In cos q dWFn (n) = ò In cos q dW

Fn (n) is the net flux in the direction of nIf In is isotropic thermal radiation, get: Fn = p In = p Bn

Flux – a vector quantity

In

Momentum Flux

The momentum of a photon is E/cMomentum flux pn in the direction of n =

photon flux times momentum per photon:

pn (n) = 1/ c ò In cos2 q dW

One factor of cos q comes from foreshortening of dA

Only the normal component of the momentum acts on the surface, hence the second factor of cos q

Units: N/m2/Hz

In

Energy density of radiation

Consider a cylinder along a ray of length c dt. Define:un (W) = energy per unit solid angle per unit volume per unit frequency in the cylinder:

dE = un (W) dV dW dv = un (W) (dA c dt) dW dvAll this radiation will exit the cylinder through dA in time dt, so:

dE = In dA dW dt dvEquating gives: un (W) = In / cIntegrating over angles, we obtain the specific energy density, un (units J/m3/Hz). This is the energy per unit volume per unit frequency interval,

un = ò un (W) d W = (1 / c) ò In dW = ( 4π/ c) JnThe total energy density of radiation requires one more integration over frequenciesand has dimensions of Energy / Volume:

u = ò un dv = (4 π / c) ò Jn dv

Moments of the Radiation Fieldn-th moment is ò In cosn q dWFirst three moments of specific intensity are named J (zeroth moment), H (first), and K (second):

∫

∫

∫

Ω=

Ω=

Ω=

dcos41

dcos41

d41

2 θπ

θπ

π

νν

νν

νν

IK

IH

IJ

Physically: J = mean intensity; H = F / 4p

K related to momentum flux: νν

π Kc

p 4=

Intensity MomentsThe moments of the radiation field are:

J – mean intensity; H – flux; K – momentum fluxCompute these moments throughout the slab. First split the slab into layers, then tally number of packets, weighted by powers of their direction cosines to obtain J, H, K. Contribution to specific intensity from a single packet is:

∫∫∫ Ω=Ω=Ω= d41d

41d

41 2µ

πµ

ππ νννννν IKIHIJ

ΔIν =ΔE

|µ |ΔAΔtΔν ΔΩ=

Fν|µ |N ΔΩ

=π Bν

|µ |N ΔΩ

Substitute into intensity moment equations and convert the integral to a summation to get:

Note the mean flux, H, is just the net energy passing each level: number of packets traveling up minus number traveling down.

Pathlength formula (Lucy 1999)Long history of use in neutronics

Jν =Bν4N

1|µi |i

∑ Hν =Bν4N

µi

|µi |i∑ Kν =

Bν4N

µi2

|µi |i∑

Ji =L

4π N ΔVil∑

Some Monte Carlo packets may pass through a cell without interacting (scatter or absorbed), but the path length estimator ensures they still contribute to the estimates for mean intensity, absorbed energy, radiation pressure, etc

Ji =L

4π N ΔVil∑

Summing path lengths gives better estimates for intensities, absorbed energy, radiation pressure, etc. More packets pass through a cell than interact with a cell

Mean intensity, J, related to photon energy density, u, via

Packet contributes a fraction en t/Dt to the energy densityof a cell where t = l/c is time the packet spends in a cell, so can form Monte Carlo estimator:

Where en = MC packet energy = L Dt / N. Hence, get estimator for J which will be accurate in optically thin regions:

Ji =L

4π N ΔVil∑

€

uν = 4π Jν /c

€

uν =1

cΔtΔVi

εν l∑

How much energy absorbed in a cell? Could count number of absorption events in each cell, but this is inaccurate for optically thin systems. We know the change in intensity for radiation passing through a medium with absorbing particles is

dI = - I n sabs dl = - I dtabs

Hence, a Monte Carlo estimator for absorbed energy:

!"abs ='

( Δ*"+,-abs .

Random Number Generators• Want random numbers in range 0 < x < 1• Generate sequence of numbers rapidly• No patterns or correlations• Pass statistical tests for randomness• Because using computer algorithms the sequence

will be periodic, so period should be as long as possible – pseudo random numbers

Anyone who considers arithmetical methods for producing random digits is, of course, in a state of sin.

John von Neumann

Random Number Generators• Pseudo random number generators PRNGs• x = ran(seed), seed usually an integer, updated in

each call to ran• Can easily de-bug Monte Carlo codes: if use same

seed for PRNG will get same random sequence• Use uniformly distributed random numbers from

(0 < x < 1) to sample from complex functions• Much research devoted to PRNGs• Computer modular arithmetic, remainders and bits

Middle Square Method• Used by von Neumann in 1940s• Recursive relation: square a n-digit number and take

the middle n digits (add zeroes to make a 2n digit number if necessary), repeat process

• e.g., n = 4:

• Problems: short period, can get stuck in very short loops, or crash (e.g., 0000)

• Von Neumann acknowledged problems, but found this fast (1940s), adequate for problems, and crashes were obvious

25682 = 06594624 gives 5946, x = 0.594659462 = 35354916 gives 3549, x = 0.354935492 = 12595401 gives 5954, x = 0.5954etc, etc

Linear Congruential Generators• Based on integer recurrence relation:

• mod(A,B) gives remainder when A divided by B

• Careful choice of a, c, M gives periods around 232 (109)

• Random number in range (0,1) from:

• ran2.f from Numerical Recipes is more complex, involving shuffling of sequences. Authors offered prize of $1000 if anyone finds a statistical test that ran2 fails.

€

yi+1 =mod(a yi + c,M)

€

ξi =yiM

Good and Bad Random Number Generators

• a = 1366, c = 150889, M = 714025• a = 137, c = 187, M = 256• “First return maps” – plot successive pairs of (xi, xi+1)

yi+1 =mod(a yi + c,M )

€

ξi =yiM

95

The first return maps for these two random number generators are shown in Figure 14.4. Note

that the first random number generator appears to have no correlations; however, the second random

number generator is correlated and shows periodic behavior. Thus, the second random number

generator would not be a good choice for actual use.

0

0.2

0.4

0.6

0.8

1

0 0.2 0.4 0.6 0.8 1

xn

xn+1

0

0.2

0.4

0.6

0.8

1

0 0.2 0.4 0.6 0.8 1

Xn

Xn+1

(a) (b)

Figure 14.4. First return maps for (a) Random Number Generator #1; (b) Random Number Generator #2.

xi xi

xi+1 xi+1

Should we worry…?

• Maybe… but if you read you’ll get scared!

• OK for our needs, need better for cryptography

• Mersenne Twister: period 219937-1 ~ 4.3 E6001