Chapter 2

Flow kinematics

Vector and tensor formulae

This introductory section presents a brief account of different definitions of vector and tensoranalysis that will be used in the following chapters. In the following, we shall consider anorthogonal coordinate system with unit vectors (e1, e2, e3) at each point. In that coordinatesystem, any vector a admits a representation as a function of three scalars ai such that a =∑

i aiei. Some common operations between two vectors a and b include the scalar producta · b =∑i aibi and the cross product

a ∧ b =

∣∣∣∣∣∣

e1 e2 e3a1 a2 a3b1 b2 b3

∣∣∣∣∣∣

= (a2b3 − a3b2)e1 + (a3b1 − a1b3)e2 + (a1b2 − a2b1)e3. (2.1)

A second-order tensor ¯A is to be interpreted in the framework of the present course as a linear op-erator that, when acting over a vector a, gives as result another vector b = ¯A · a with componentsbi =

∑

j Aijaj. The transverse tensor ¯AT, with components ( ¯AT)ij = ( ¯A)ji, satisfies a· ¯A = ¯AT ·a.The tensor ¯I with components Iii = 1 y Iij = 0 if i 6= j is the so-called identity tensor, which

verifies ¯I · a = a for any given vector a. Of interest in the following development are the dyadicproduct of two vectors, ab, which produces a tensor of components (ab)ij = aibj , and the

contraction of two tensors, ¯A : ¯B which gives as a result a scalar ¯A : ¯B =∑

i

∑

j AijBij .

Note that this last result is quite different from the product of the two tensors, ¯A · ¯B, which isanother tensor of components ( ¯A · ¯B)ij =

∑

kAikBkj.Also of interest is the cross product of a

vector a = (a1, a2, a3) and a tensor ¯A, which gives a tensor according to

a ∧ ¯A =

0 −a3 a2a3 0 −a1−a2 a1 0

¯A. (2.2)

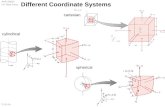
Besides cartesian (rectangular) coordinates (x1 = x, x2 = y, x3 = z), two other types oforthogonal curvilinear coordinates will be found to be useful: cylindrical coordinates (x1 = r,x2 = θ, x3 = z) and spherical coordinates (x1 = r, x2 = θ, x3 = φ), which are schematicallyrepresented in Fig. 2.1, along with their associated unit vectors (e1, e2, e3).

Kinematics

er

eθ

eφ

r

θ

φ

ez

eθ

er

y

ez

e

e

xθ

ry

z

x

Figure 2.1: Schematic representation of relevant coordinate systems.

The differential line elements associated for each of the three coordinate systems considered are,respectively, dx = (dx,dy,dz), dx = (dr, rdθ,dz) and dx = (dr, rdθ, rsinθdφ). The coefficientsthat premultiply each of the differentials in the above expressions are the so-called scale factors(h1, h2, h3), which reduce to (h1 = 1, h2 = 1, h3 = 1) for cartesian coordinates, to (h1 = 1, h2 =r, h3 = 1) for cylindrical coordinates, and to (h1 = 1, h2 = r, h3 = rsinθ) for spherical coordinates.The introduction of these scale factors enables the differential operators to be written in acompact form independent of the coordinate system. Thus, the gradient of a scalar functionΦ is in general given by

∇Φ =

(1

h1

∂Φ

∂x1,1

h2

∂Φ

∂x2,1

h3

∂Φ

∂x3

)

, (2.3)

while its laplacian can be expressed in the form

∇2Φ =1

h1h2h3

[∂

∂x1

(h2h3h1

∂Φ

∂x1

)

+∂

∂x2

(h1h3h2

∂Φ

∂x2

)

+∂

∂x3

(h1h2h3

∂Φ

∂x3

)]

. (2.4)

Similarly, the divergence of a vector function a = a1e1 + a2e2 + a3e3 is

∇ · a =1

h1h2h3

[∂

∂x1(h2h3a1) +

∂

∂x2(h1h3a2) +

∂

∂x3(h1h2a3)

]

, (2.5)

while its curl is given by

∇∧ a = 1h1h2h3

∣∣∣∣∣∣

h1e1 h2e2 h3e3∂

∂x1

∂∂x2

∂∂x3

h1a1 h2a2 h3a3

∣∣∣∣∣∣

= 1h2h3

[∂

∂x2(h3a3)− ∂

∂x3(h2a2)

]

e1+

1h1h3

[∂

∂x3(h1a1)− ∂

∂x1(h3a3)

]

e2 +1

h1h2

[∂

∂x1(h2a2)− ∂

∂x2(h1a1)

]

e3.

(2.6)

Also, the gradient of a vector function produces a tensor according to

(∇a)ii =1

hi

∂ai∂xi

+∑

k 6=i

akhihk

∂hi∂xk

and (∇a)ij =1

hi

∂aj∂xi

− aihihj

∂hi∂xj

if i 6= j, (2.7)

10

Kinematics

while the divergence of a tensor ∇ · ¯A gives a vector function of components

(∇ · ¯A)i =hih

∑

j

∂

∂xj

(hAij

hihj

)

+∑

j

Aij +Aji

hihj

∂hi∂xj

−∑

j

Ajj

hihj

∂hj∂xi

, (2.8)

where h = h1h2h3.The so-called Gauss formula ∫

Σ(n φ)dσ =

∫

V(∇ φ)dV, (2.9)

where φ represents a scalar, vector or tensor function, V is a domain enclosed by the closed surfaceΣ, and denotes any of the products defined above, will be found to be useful in manipulatingthe conservation equations.

Some preliminary concepts

Two different approaches, called respectively Eulerian and Lagrangian descriptions, can beadopted when describing the velocity field. The Lagrangian approach takes a discrete point ofview by treating the fluid as an ensemble of fluid particles. The flow field is described in termsof the fluid-particle trajectories

x = xT(t; xo, to), (2.10)

with each fluid particle identified by its initial position xo at the initial time time to. Theassociated velocity and acceleration is computed by straightforward derivation to give v = dxT/dtand a = d2xT/dt

2. This Lagrangian approximation, which might be of use in specific applications(e.g., for the analysis of the disperse phase in two-phase problems), leads in general to complexconservation laws. For that reason, in the following derivation we shall adopt instead the Euleriandescription, which assumes the velocity to be a continuous vector field v(x, t) as a function ofthe position x and time t.A flow field is said to be uniform when the spatial differences of the different flow properties arestrictly zero. Similarly, a fluid flow is said to be steady when it does not change in time. Thus, auniform velocity field satisfies v = v(t), whereas whereas a steady velocity field is such thatv = v(x). At times, the steadiness of a given flow depends on the observer. For instance, for aflow over an aircraft moving with constant velocity, the flow is clearly unsteady for an observerstanding on the ground, whereas for the pilot the flow is effectively steady. A moving frame ofreference in that case would clearly facilitate the analysis of the flow.A stagnation point is defined as a point where the velocity is zero (all three components). For agiven velocity field v = v(x, t), the stagnation points are determined by the equation

v(x, t) = 0. (2.11)

Clearly, the location of the stagnation points depends on the reference frame selected.

Trajectories, path lines, and streak lines

In its motion, a fluid particle initially located at x = xo changes its position in time as expressedin (2.10). Given the velocity field v(x, t), the location of the fluid particle at each instant of timeis determined by integration of

dx

dt= v(x, t) (2.12)

11

Kinematics

with initial condition x = xo at t = to to give x = xT(t; xo, to). The above vector equation canbe alternatively expressed in its three components

dt =h1dx1

v1(x1, x2, x3, t)=

h2dx2v2(x1, x2, x3, t)

=h3dx3

v3(x1, x2, x3, t)(2.13)

to be integrated subject to x1 = x1o , x2 = x2o and x3 = x3o at t = to. The solution can beexpressed in the general form (2.10), which reduces to

x = xT(t;xo, yo, zo, to)

y = yT(t;xo, yo, zo, to) (2.14)

z = zT(t;xo, yo, zo, to)

for cartesian coordinates.The trajectory contains information about the path followed by the particle and also about therate with which it travels along it. The equations that describe the path lines can be obtainedby eliminating the time in (2.10). For instance, for cartesian coordinates, once the time has beeneliminated in (2.14), the following two equations emerge

f(xo, yo, zo, to, x, y, z) = g(xo, yo, zo, to, x, y, z) = 0 (2.15)

defining two surfaces whose intersection is the path line followed by the fluid particle initiallylocated at (xo, yo, zo).Besides path lines, in connection with the particle trajectories it is of interest to introducethe concept of streak lines. At a given time t = t∗, consider the fluid particles that havepassed through the point x = xo at an earlier time to. These particles lie on a curve, thatwe call streak line. They are useful in experiments for observational purposes; they can bevisualized by injecting dye slowly at some fixed point. Its mathematical description readilyfollows from evaluating the equations for the particle trajectories (2.14) at a fixed time t = t∗

for varying to. Eliminating to from the three equations provides the alternative descriptionF(xo, yo, zo, t

∗, x, y, z) = G(xo, yo, zo, t∗, x, y, z) = 0 in terms of two intersecting surfaces.

Fluid lines, fluid surfaces and fluid volumes

Fluid particles initially located along the curve

x = xl(λ), (2.16)

where λ denotes a parameter describing the curve 1, will continue to form a curve at any sub-sequent time. The equation describing the evolution of a fluid line is obtained by writing theequation for the trajectories, given in (2.10), for the fluid particles located at the initial timet = to along the curve defined in (2.16) to yield

x = xT(xl(λ), t). (2.17)

1Recall that a curve can be in general expressed in the parametric form x = xl(λ) with λ1 < λ < λ2.For instance, the vertical axis is given by the expression x = 0, y = 0, z = λ (−∞ < λ < ∞), while theparametric expression for a circle of radius R contained on the horizontal plane and centered at the origin isx = R cos λ, y = R sinλ, z = 0 (0 < λ < 2π).

12

Kinematics

Similarly, fluid particles initially forming a surface

x = xs(α, β), (2.18)

where α and β are parameters2 will continue to form a surface (fluid surface). The correspond-ing fluid-surface equation

x = xT(xs(α, β), t), (2.19)

can be simplified by eliminating the parameters α and β, yielding in general an implicit equationof the form

f(x, t) = 0. (2.20)

If the surface is initially closed, it can be expected to remain closed in its evolution. The finitevolume of fluid bounded by a closed fluid surface is called a fluid volume, a useful conceptto be used later when deriving the conservation laws governing the fluid motion. In particular,in view of the definition of the fluid velocity as the velocity of the center of mass of the fluidparticle (see (1.4)), it is clear that mass cannot cross a fluid surface, which implies that themass of a fluid volume remains constant, thereby providing the first conservation law offluid mechanics.

Streamlines, stream surfaces and stream tubes

The streamlines of a flow field at a given instant of time t = t∗ are lines that are tangent tothe local velocity vector at each point. This tangency condition can be expressed in the form

h1dx1v1(x1, x2, x3, t∗)

=h2dx2

v2(x1, x2, x3, t∗)=

h3dx3v3(x1, x2, x3, t∗)

(2.21)

The two integration constants for the above pair of differential equations serve to identify a spe-cific streamline. For instance, one could identify a streamline by selecting the location (xo, yo)at which it crosses the horizontal plane z = 0. If two streamlines intersect, the crossing point isnecessarily a stagnation point (why?). There are two additional concepts related to the stream-lines that are worth mentioning. The surface formed by all streamlines intersecting a given lineis called a stream surface. If the line selected is closed, the resulting stream surface wouldform a stream tube.

Although Eqs. (2.13) and (2.21) look similar, they represent two very different physical andmathematical concepts. The time t is an integration variable in the initial value problem definedby (2.13), whereas it merely plays the role of a parameter in the integration of (2.21). To find atrajectory, we follow the temporal evolution of the fluid particle. To find a streamline, we freeze

the time by looking at the velocity field existing at a specific instant.

Path lines and streamlines differ in a general unsteady flow. However, for a steady velocity fieldv = v(x) or, more generally, for a velocity field of the form v = f(t)V (x) with f(t) representingan arbitrary function of time, streamlines and path lines can be shown to coincide (show it!).

2In general, a surface can be defined in terms of a pair of parameters. For instance, a sphere of radius R centeredat the origin admits the parametric representation x = R sinα cos β, y = R sinα sin β, z = R cosα (0 < α < π,0 < β < 2π).

13

Kinematics

Material derivative

To determine the variation of any intensive scalar property φ following the fluid flow, suchas the density, pressure or temperature, one must account for the fluid motion by consideringthe infinitesimal displacement of a fluid particle, as illustrated in Fig. 2.2. At time t the fluid

dt + tt

xx + xd

xd

Figure 2.2: Infinitesimal displacement of a fluid particle.

particle is located at x, so that the initial value of the intensive property is given by φ(x, t).A time increment dt later, the particle has moved to occupy a new position given by x + dx(dx = vdt), and the new value of φ would be given by φ(x+ dx, t+ dt). Neglecting small termsin a Taylor expansion of φ about (x, t) enables the variation of φ for the fluid particle to bewritten in the approximate form

dφ = φ(x+ dx, t+ dt)− φ(x, t) = dt∂φ

∂t+ dx · ∇φ. (2.22)

Dividing the above expression by dt and identifying v = dx/dt leads to

Dφ

Dt=∂φ

∂t+ v · ∇φ, (2.23)

where the material derivative operator

D()

Dt=∂()

∂t+ v · ∇() (2.24)

expresses the variation in time of any intensive scalar property following the fluid particle. Thefirst term on the right-hand side represents the local temporal variation, while the second termis the so-called convective derivative, related to the motion of the fluid particle. Changes in theproperties of a fluid particle may arise because the flow is unsteady and/or because the fluidparticle moves through a nonuniform field 3.

3Note that the concept of material derivative serves to derive the differential equation to be satisfied by thefunction f(x, t) corresponding to the fluid surface f(x, t) = 0 (see Eq. (2.20)). The fluid surface therefore dividesthe flow field in two regions where the sign of f(x, t) is different. Since the fluid particles defining the fluid surfacemaintain a constant value f(x, t) = 0 in their evolution, the function f(x, t) must satisfy the equation

Df

Dt=

∂f

∂t+ v · ∇f = 0.

14

Kinematics

Acceleration

The concept of material derivative can be extended to determine the time evolution of a vectorproperty. In particular, we shall define the acceleration vector as

a =Dv

Dt=∂v

∂t+ v · (∇v), (2.25)

where the gradient of velocity ∇v is a tensor. A convenient way to express (2.25) is

a =∂v

∂t+∇(|v|2/2)− v ∧ (∇ ∧ v), (2.26)

which is valid regardless of the coordinate system selected.

In cartesian coordinates, the components of the gradient of velocity are given by (∇v)ij =∂vj/∂xi, so that each component of the acceleration ai reduces to the material derivative of thecorresponding velocity component according to

ai =DviDt

=∂vi∂t

+ vj∂vi∂xj

. (2.27)

Note that this last result does not hold when cylindrical or spherical coordinates are used.

For the description of certain flow fields, it is at times convenient to employ a non-inertialreference frame, that is, a reference frame that is accelerating and/or rotating with respect tothe laboratory frame of reference. In that case, when writing the fluid acceleration one mustaccount for the additional inertial contribution

as = ao +dΩ

dt∧ x+ Ω ∧ (Ω ∧ x) + 2Ω ∧ v, (2.28)

where ao and Ω are the acceleration and angular velocity of the non-inertial reference frame.

Circulation and vorticity

The circulation Γ along a curve L is defined as the integral

Γ =

∫

Lv · dl, (2.29)

where the vector dl represents the differential line element. Physically, the circulation gives as ameasure of the fluid motion along the direction of the curve. If x = xl(λ) (λ1 < λ < λ2) is theparametric representation of the curve, then

dl =dxldλ

dλ, (2.30)

so that (2.29) reduces to

Γ =

∫

Lv(x, t) · dl =

∫ λ2

λ1

v(xl(λ), t) ·dxldλ

dλ. (2.31)

15

Kinematics

If one considers a closed curve, then according to Stokes theorem

Γ =

∮

Lv · dl =

∫

Σ(∇∧ v) · ndσ, (2.32)

where Σ represents any surface bounded by L and dσ is a surface differential element with normalunit vector n, defined for the surface to have positive orientation according to the so-called right-hand rule; see Fig. 2.3. For the last equation to hold, the velocity field v(x, t) must be continuousand the surface Σ must be completely contained within the fluid domain. The vector ω = ∇∧ vis called vorticity.

σ

L

n

Σ

Figure 2.3: Application of Stokes theorem for the computation of the circulation.

The circulation along a closed curve limiting an infinitesimally small surface dσ contained in aplane normal to n reduces to ∮

Lv · dl = (∇ ∧ v) · ndσ. (2.33)

Hence, (∇ ∧ v)n = (∇ ∧ v) · n turns out to be the circulation per unit surface around a curvenormal to n. At a given point, the circulation will be maximum when the curve is contained ina plane normal to ∇∧ v.

Irrotational flow and velocity potential

The fluid motion is said to be irrotational when the vorticity is identically zero everywhere, i.e.,ω = ∇ ∧ v = 0. In vector calculus we have seen that for any irrotational vector field one candefine a scalar function, called potential function, such that

v = ∇ϕ. (2.34)

The potential is defined by (2.34), except for an integration constant, whose value, a function oftime, can be selected arbitrarily. Clearly, the introduction of the velocity potential will simplifynotably the description of irrotational motions, because we are effectively replacing the compu-tation of a three-component vector field (the velocity v) by that of a scalar field (the potentialϕ).If the circulation along any closed curve is zero, the flow is necessarily irrotational. The demon-stration begins by considering an infinitesimally small closed curve around a given point. Ac-cording to (2.33), the circulation around the curve will be zero, regardless of the orientation n, if

16

Kinematics

∇∧ v = 0. The opposite is not necessarily true, that is, even though ∇∧ v = 0 everywhere in theflow field, the circulation around a closed curve might not be zero. This is so because the validityof (2.32) is restricted to surfaces Σ that are completely contained in the fluid domain. Therefore,for an irrotational field, one can claim that the circulation around a given closed curve is zero ifand only if we can find a surface bounded by the curve that is completely contained in the flowfield, that is, when the curve is continuously reducible to a point (the fluid domain is simplyconnected). This feature of irrotational motion arises in the study of flows over airfoils, relevantto the design of wings, compressor and turbine blades, etc. In the two-dimensional flow fieldthat appears, the circulation around a closed curve circling the airfoil - which is non-reducibleto a point - is non-zero, and turns out to be linearly proportional to the lift force provided bythe airfoil.

Convective flux

Mass, momentum and energy are transported by the moving fluid. To quantify in general thistransport rate, we introduce φ(x, t) to represent a given fluid property expressed per unit volume,with particular cases of interest being the mass, momentum and energy per unit volume (φ = ρ,φ = ρv and φ = ρ(e + |v|2/2)). With this definition, the total amount of a given quantityexisting within a given volume V is given by

∫

V φdV (e.g., the total amount of mass containedin a volume is

∫

V ρdV ).

Let us now consider the fixed surface Σo shown in the figure. The fluid will cross the surface inits motion, transporting across mass, momentum and energy. The volume of fluid crossing in a

σd

dtv

o

n

Σ

Figure 2.4: Convective flux.

time dt through the differential surface element dσ oriented perpendicular to n is that containedin the parallelepiped of base dσ and side vdt shown in the figure, which can be computed asv · ndσdt. The amount of mass, momentum and energy crossing with the fluid is therefore givenby φv · ndσdt, and the total convective flux across the surface (mass, momentum or energy thatcrosses the surface per unit time) is obtained by adding the contribution of the different surface

17

Kinematics

elements and dividing the result by the unit time dt to give

∫

Σo

φv · ndσ. (2.35)

Note that, with φ = 1, the above integral serves to compute the volume of fluid that crosses Σo

per unit time, the volume flux

Q =

∫

Σo

v · ndσ. (2.36)

When φ = v, we find inside the integral (2.35) the so-called momentum flux tensor ρvv.

If Σo is a closed surface (and φv is a continuous function), Gauss formula (2.9) enables theconvective flux to be written in the form

∫

Σo

φv · ndσ =

∫

Vo

∇ · (φv)dV, (2.37)

where Vo is the volume bounded by Σo. If we now consider an infinitesimally small volume, itthen follows that ∇ · (φv) is the rate at which mass, momentum or energy abandons the unitvolume due to the fluid outflow. Similarly, ∇ · v is the amount of volume that abandons theunit volume per unit time (the expansion rate). Note that, for a perfect liquid, whose density isstrictly constant, the condition that the specific volume cannot change requires that the condition

∇ · v = 0 (2.38)

be satisfied at each point.

The concept of convective flux can be extended to a moving surface Σc(t) whose points aremoving with velocity vc(xc, t) by replacing the fluid velocity v with the relative velocity v − vcwhen computing the flux to give ∫

Σc(t)φ(v − vc) · ndσ. (2.39)

The stream function

The description of flows that are either planar or axisymmetric can be simplified when the velocityfield is solenoidal (i.e., satisfies ∇· v = 0), as occurs in constant-density fluids (see the discussionleading to (2.63)). To present the development, we restrict our attention to the case of a planarflow described in a cartesian x− y coordinate system. Extensions to steady gas flow, for whichthe continuity equation becomes ∇ · (ρv) = 0, and also to polar coordinates and axisymmetricflows can be performed, but will not be considered further in this introductory section.

For a planar flow ∇ · v = 0 reduces to

∂vx∂x

+∂vy∂y

= 0. (2.40)

To solve the problem, it is convenient to introduce a scalar function ψ, called stream functiondefined from the two equations

vx =∂ψ

∂yand vy = −∂ψ

∂x, (2.41)

18

Kinematics

which determine ψ upon integration, except for an arbitrary additive constant. Straightforwardsubstitution of (2.41) into (2.40) reveals that the velocity field deriving from a stream functionsatisfies automatically the condition of zero expansion rate. An important property of the streamfunction is that the isolines ψ = constant are streamlines, as can be seen by noticing that alongan isoline

dψ =∂ψ

∂xdx+

∂ψ

∂ydy = −vydx+ vxdy = 0. (2.42)

The last of these equations can be written as

dx

vx=

dy

vy, (2.43)

corresponding to the planar counterpart of (2.21), thereby demonstrating that isolines andstreamlines coincide.Another useful property of ψ is that the difference ψ2 − ψ1 between the value of the streamfunction corresponding to two different streamlines equals the volumetric flux (2.36) for theplanar stream tube defined by the two streamlines. Given a curve with end points on each one

n

n

2

ψ2

ψ1

1

Figure 2.5: Volumetric flux between two streamlines.

of the streamlines, as shown in the figure, the value of ψ2 − ψ1 is given by the integral

ψ2 − ψ1 =

∫ 2

1dψ =

∫ 2

1(−vydx+ vxdy), (2.44)

as can be seen from (2.42). Bearing in mind that (dy,−dx) = ndl, where n is the unit vectornormal to the integration curve, the previous equation can finally be rewritten in the form

ψ2 − ψ1 =

∫ 2

1v · ndl, (2.45)

where the integral on the right-hand side is the volumetric flux between the two stream surfacesconsidered (per unit length perpendicular to the plane)

Relative motion near a point

As previously mentioned, the force exerted by a portion of fluid on an adjacent portion of fluidis proportional to the rate at which the fluid is being deformed. To determine that rate, let us

19

Kinematics

consider the motion of a differential element of fluid line dx, whose ends are initially located at xand x+dx. The velocities of these two ends differ by a small amount dv, which can be expressedin the first approximation as

dv = dx · ∇v (2.46)

in terms of the gradient of velocity ∇v. After an infinitesimally small time dt, the two ends of thefluid line element have moved to occupy new positions given by x+ vdt and x+dx+(v+dv)dt,respectively. Clearly, besides a translation vdt, the fluid element has undergone a distortion,with dx becoming dx+ dvdt, as indicated in Fig. 2.6.

xd

dv t

dv t dv t+ d

dv td dd

d

v tr d

dv t

Figure 2.6: Motion of a differential element of fluid line.

The geometrical character of dvdt = dx · ∇vdt is best investigated by decomposing the velocitygradient into parts that are symmetric and anti-symmetric, according to

∇v =1

2(∇v +∇vT) +

1

2(∇v −∇vT) = ¯Td +

¯Tr. (2.47)

where the symmetric tensor ¯Td is called the rate-of-strain tensor and the anti-symmetric tensor¯Tr is called the rotation tensor. In cartesian coordinates, the two tensors ¯Td and ¯Tr can becomputed according to

¯Td =

∂v1∂x1

12

(∂v2∂x1

+ ∂v1∂x2

)12

(∂v3∂x1

+ ∂v1∂x3

)

12

(∂v2∂x1

+ ∂v1∂x2

)∂v2∂x2

12

(∂v3∂x2

+ ∂v2∂x3

)

12

(∂v3∂x1

+ ∂v1∂x3

)12

(∂v3∂x2

+ ∂v2∂x3

)∂v3∂x3

(2.48)

and

¯Tr =

0 12

(∂v2∂x1

− ∂v1∂x2

)12

(∂v3∂x1

− ∂v1∂x3

)

−12

(∂v2∂x1

− ∂v1∂x2

)

0 12

(∂v3∂x2

− ∂v2∂x3

)

−12

(∂v3∂x1

− ∂v1∂x3

)

−12

(∂v3∂x2

− ∂v2∂x3

)

0

(2.49)

20

Kinematics

This last expression can be rewritten in the form

¯Tr =1

2

0 ω3 −ω2

−ω3 0 ω1

ω2 −ω1 0

, (2.50)

in terms of the three components ω1, ω2 and ω3 of the vorticity vector ω = ∇∧ v.Introducing (2.47) into (2.46) yields

dv = dx · ¯Td + dx · ¯Tr = dvd + dvr. (2.51)

The contribution of the anti-symmetric tensor ¯Tr corresponds to a rotation of the fluid elementdx with angular velocity (∇∧ v)/2, as can be seen by writing dvr in the form

dvr = dx · ¯Tr =1

2(∇∧ v) ∧ dx =

1

2ω ∧ dx. (2.52)

Thus, if ¯Td were identically zero, the motion of the fluid would be exactly that of a rigid body,that is, exclusively translation and rotation.

On the other hand, the symmetry of the rate-of-strain tensor ¯Td enables dvd = dx · ¯Td to bewritten in the form

dvd = ¯Td · n ds, (2.53)

where the differential fluid element has been expressed as dx = nds in terms of its differentiallength ds and the unit vector n. In general, the strain rate is not aligned with n, implying thatthe element dx undergoes both extension and shear strain. The magnitude of the extension rateis given by the scalar product n · ¯Td · n ds, so that n · ¯Td · n represents the extension rate per unitlength along the direction defined by n. On the other hand, the contribution of dvd to the sheardeformation is obtained by appropriately subtracting from the total strain rate the extensionrate according to [ ¯Td · n− (n · ¯Td · n) n]ds.There are three privileged directions of space, called principal directions of strain, along whichthe strain reduces to an extension, without any shear strain (the resulting vector dvd is parallelto n). These principal directions n1, n2 and n3, and their corresponding strain rates, λ1, λ2 andλ3, are computed by solving the eigenvalue problem

¯Td · n = λ n. (2.54)

In particular, the characteristic equation that determines λi,

| ¯Td − λ ¯I| = 0 (2.55)

follows from imposing the existence of nontrivial solutions. The symmetry of the tensor ¯Td

guarantees the existence of three real roots for this equation, associated with three mutuallyperpendicular principal directions. Obviously, in the local reference frame defined by the threedirections ni the associated rate-of-strain tensor becomes diagonal, with diagonal componentsλ1, λ2 and λ3.

21

Kinematics

v

l dt

dl dt

dl dt

dl dt

dl dt

dl dt∂∂x

1

1

vdl

∂∂x

1

2

(21

∂∂x

1

2)

1∂∂x

2

(21

∂∂x

1

2)+

1∂∂x

2

∂∂x

2

2

∂∂x1

2v v

v

v

v

v

d

Figure 2.7: Deformation and rotation of an infinitesimally small fluid element of square shape.

Deformation of a square fluid element

Let us now consider the evolution of a square fluid element. The two sides, of initial length dl,evolve after a time dt from dl to dl+ dl · ∇vdt, so that

dl · ∇v = dl(1, 0)

∂v1∂x1

∂v2∂x1

∂v1∂x2

∂v2∂x2

= dl

(∂v1∂x1

,∂v2∂x1

)

(2.56)

and

dl · ∇v = dl(0, 1)

∂v1∂x1

∂v2∂x1

∂v1∂x2

∂v2∂x2

= dl

(∂v1∂x2

,∂v2∂x2

)

(2.57)

The observation of Fig. 2.7 helps to reveal the physical meaning of each of the terms appearingin the tensors

¯Td =

∂v1∂x1

12

(∂v2∂x1

+ ∂v1∂x2

)

12

(∂v2∂x1

+ ∂v1∂x2

)∂v2∂x2

(2.58)

and

¯Tr =

0 12

(∂v2∂x1

− ∂v1∂x2

)

−12

(∂v2∂x1

− ∂v1∂x2

)

0

(2.59)

Recalling that the decomposition dl · ∇vdt = dvddt + dvrdt applies, with dvd = dl · ¯Td and

22

Kinematics

dvr = dl · ¯Tr, one obtains for the horizontal side dl(1, 0)

dvd = dl

[∂v1∂x1

,1

2

(∂v2∂x1

+∂v1∂x2

)]

and dvr = dl

[

0,1

2

(∂v2∂x1

− ∂v1∂x2

)]

, (2.60)

whereas for the vertical side

dvd = dl

[1

2

(∂v2∂x1

+∂v1∂x2

)

,∂v2∂x2

]

and dvr = dl

[

−1

2

(∂v2∂x1

− ∂v1∂x2

)

, 0

]

. (2.61)

According to the figure, the elements along the diagonal of the rate-of-strain tensor representthe rate of extension per unit length in the directions of the three axes. Besides, the sideshave undergone rotations of angles dt(∂v2/∂x1) and −dt(∂v1/∂x2), so that the average angularvelocity for the square element in its plane is given by 1

2(∂v2/∂x1 − ∂v1/∂x2). Therefore, the

off-diagonal elements of the anti-symmetric tensor ¯Tr represent the three components of theangular velocity of the fluid element. On the other hand, the angle formed by the fluid-elementsides, initially perpendicular, have decreased an amount (∂v2/∂x1 + ∂v1/∂x2)dt, indicating that(∂v2/∂x1+∂v1/∂x2) is the shear strain rate (the rate at which the angle formed by the directions1 and 2 is decreasing). In other words, the off-diagonal components in ¯Td correspond to half ofthe shear strain rate perpendicular to the three axis of the reference frame.

Deformation of a cubic fluid element

t

d t

d t d t

d t

d t

d t

d t

d t

d

l

1vd

1vd

2

3

d v2d v23 1

d v

d v

d 2v3 1 3

33

1v1d

d 2v2

l

l

l

l l

l

l

l

Figure 2.8: Deformation and rotation of a cubic fluid element of infinitesimally small size.

The above figure considers the evolution of an infinitesimally small fluid element of cubic shape,with the simplified notation ∂ivj = ∂vj/∂xi adopted for convenience. The discussion given abovefor the square shape also applies here. In this case, the distortion of the fluid element associatedwith the straining motion produces a variation of volume from its initial value dl3. After adifferential time dt, the new volume is given by

dl3

∣∣∣∣∣∣

1 + ∂1v1dt ∂1v2dt ∂1v3dt∂2v1dt 1 + ∂2v2dt ∂2v3dt∂3v1dt ∂3v2dt 1 + ∂3v3dt

∣∣∣∣∣∣

≃ dl3 + dl3dt(∂1v1 + ∂2v2 + ∂3v3), (2.62)

23

Kinematics

after small terms of order dt2 and dt3 are neglected. The previous equation reveals that thevelocity divergence ∇· v = ∂1v1+∂2v2+∂3v3 represents physically the rate at which the volumeof the fluid element is changing per unit volume. This quantity ∇ · v, equal to the trace of thetensors ∇v and ¯Td, is called rate of expansion or dilatation rate. For a perfect liquid, forwhich the volume of the fluid element does not change since the density is constant, the velocityfield must satisfy

∇ · v = 0, (2.63)

a result that was anticipated earlier. Clearly, for the dilatation rate to be zero, the linearextension rates ∂1v1, ∂2v2 and ∂3v3 cannot all three have the same sign. In other words, for thevolume of an incompressible fluid particle to remain constant, a positive extension rate appearsin one or two directions, with a compensating compression rate appearing in the other one (ortwo) directions to give a zero net expansion rate.

24