PHYSICAL REVIEW 0 VOLUME 38, NUMBER 8 15 OCTOBER 1988

Optimized expansion in quantum field theory of massive fermionswith (ff) interaction

Anna OkopinskaInstitute ofPhysics, Warsaw Uniuersity, BiaIystok Branch, 15-424 Bia@stok, Lipowa 41, Poland

(Received 29 October 1987)

The optimized expansion for the generating functional for Green s functions in the path-integralrepresentation is formulated in quantum field theory of fermions with a scalar Fermi interaction and

compared with different expansion techniques. The effective action in n-dimensional space-time is

calculated to the first order. Renormalization can be performed if the space-time dimension is less

than four. In this case, the renormalized effective potential at a finite temperature is calculated tofirst order. The results suggest that the theory in two- and three-dimensional space-time is nonin-

teracting or precarious.

I. INTRODUCTION

Quantum field theory (QFT) of a massless spinor field Pwith a scalar Fermi interaction (g1(t) has been proposed

by Heisenberg' as a candidate for a unified theory of in-

teractions. The lack of progress in developing theHeisenberg nonlinear theory is due to its perturbativenonrenormalizability in four-dimensional space-time.Even with the use of nonperturbative methods, Heisen-

berg and his co-workers' were not able to extract a physi-cal content of the theory. Renewed interest in (fP)QFT was inspired by the work of Nambu and Jona-Lasinio, who demonstrated that a fermion mass can begenerated dynamically, in analogy with the energy gap in

the microscopic theory of superconductivity. However,the value of the fermion mass, determined self-

consistently, is cutoff dependent and appears infinite, ifthe dimension of space-time is greater than two, i.e.,when the (Pg) QFT is perturbatively nonrenormalizable.The theory of X massless fermions in two dimensions hasbeen solved by Gross and Neveu in the N~ ~ limit andfermion mass generation has been shown. Recently, adynamical mass generation for the Gross-Neveu modelwith any number of fields has been shown by Latorre andSoto in the Gaussian-effective-potential approximation.

In this work we will study the effective action in Fermitheory, extending the method of the optimized expansion(OE), developed in scalar QFT with A,y interaction. Weconsider a massive fermion theory in n-dimensional Eu-clidean space with a classical action obtained by an ordi-nary Wick rotation:

N d N d

S[Q,f]= f d "x g g g'~(x)(tl~s+m5~it)fit(x)+ ~ g g p'~(x)g'~(x)i =1 A, 8=1 2X i=1 3=1

r[y, y]=lnZ [q, q] (1.3)

where f and g are independent Grassmann fields with anumber of Dirac components d =2("~ . The symbol iIdenotes y"t)„with Dirac matrices satisfying ty", y']=25 . In the following, for notational simplicity, thespace arguments and the integrations over them will besuppressed. Also discrete indices and summation overthem are shown only if necessary.

Quantization is done by representing the generatingfunctional for Green's functions as a path integral overthe fields:

Z[Fl, 'tl]= fDQDpe"P( —S[g,g]+f tl+ tip) '(1.2')

with Grass mann sources g and g introduced. Theeffective action is given by

The background fields defined by means of left variationalderivatives as

5 lnZ 5 lnZand

59 58(1.4)

y(y q)1 r[ p& pl

d "xf, /= const

(1.5)

are the vacuum expectation values of Grassmann fields inthe presence of external sources. When the sources areturned off the background Grassmann fields should van-ish, since Lorentz invariance is not expected to be bro-ken. Therefore, the one-particle-irreducible (1PI) Green'sfunctions are taken as derivatives of the effective actionat g, /=0. The effective potential into one field definedas

38 2507 1988 The American Physical Society

2508 ANNA OKOPINSKA 38

generates 1PI vertices at vanishing external momenta andis useful to study vacuum structure and renormalizedmasses and couplings.

In the path-integral approach the statistical fieldtheory of equilibrium can be treated in a similar way asvacuum Euclidean QFT. The same path integral (1.2)with appropriate boundary conditions can be used torepresent a finite-temperature generating functional,which gives a partition function at the temperature T. Inthe imaginary-time formalism the integral is taken overthe functions with periodic (antiperiodic) boundary con-ditions for boson (fermion) fields, with a period T ' inthe time coordinate. For T=O the period becomesinfinite and the partition function becomes the generatingfunctional for Green's functions with vanishing externalmomenta in vacuum QFT. The finite-temperatureeffective potential is defined by Eq. (1.5) and can be ex-pressed by momentum integrals with the aid of theFourier transform. In vacuum QFT the integral (1.2) istaken over all functions in Euclidean space; therefore, theFourier transform is given by an integral over

(1.6)

In equilibrium thermodynamics of Fermi fields the in-

tegral in (1.2) is taken over antiperiodic functions with aperiod T '. Therefore, the momentum vector p has animaginary-time component pa = ( 2j + 1 )nT, where

j =0,+1, . . . , and the Fourier transform becomes acombined sum over j and integral in ( v = n —1)-dimensional momentum space:

refJ

(1.7)

Generally, the path integral for generating functional(1.2) cannot be evaluated analytically; therefore, sys-tematic methods of approximation are developed. ForBose fields the steepest-descent method proves to be veryuseful to represent the path integral for generating func-tional as a series of calculable Gaussian functional in-tegrals. It is remarkable that a path integral for Fermifields bears some similarities with the Bose one. TheGaussian integrals are calculable and the results are verysimilar as in the bosonic case, in spite of so different a na-ture of the Grassmannian integration. Although there isno justification that the mean contribution to the integralcomes from the stationary point of the exponential, thesteepest-descent method "works" also in the fermioniccase. As discussed in Sec. II, similarly as for bosonfields, the steepest-descent method can be used in theQFT of N fields with a Fermi interaction to generate (a)the conventional loop expansion (LE), (b) the optimizedexpansion (QE), and (c) the mean-field (MF) expansion. 'In the above expansions the effective potential and all 1PIvertices given by the derivatives of the effective action at/=/=0 can be found in terms of ordinary integrals inmomentum space. The finite-temperature effective poten-tial in any expansion generated by the steepest-descentmethod has the same structure as the effective potentialand can be obtained after replacing the integrals (1.6) by

II. FORMAL METHODS OF EVALUATIONOF THE EFFECTIVE ACTION

The steepest-descent method for the path integral (1.2}consists in translating the integration variables P by g,and f by g, which minimize the exponent:

6S 6Sand

fiitj 6$(2.1)

Z[J] as a series in a formal parameter is obtained afterexpanding the exponential into a Taylor series and per-forming the Gaussian integration term by term. Theeffective action, to the given order in the formal parame-

(1.7) in the given order approximation. Just as for bosontheories, the LE gives a conventional perturbationtheory; the MF expansion is equivalent to the large-N ex-pansion (with N set equal to the number of fields). Theeffective potential in the first-order OE for Fermi theorycoincides with the Gaussian effective potential obtainedusing the variational principle for the functionalSchrodinger equation. The method is an extension ofthe Gaussian effective potential studied in A,y QFT(Refs. 9 and 10}.

Renormalizability of the theory requires the effectivepotential and vertices at arbitrary momenta to be finite.In the variational approach only the effective potential iscalculated. To find the vertices the effective action has tobe calculated. It can be done using a time-dependentvariational principle, but the Schrodinger approach is notconvenient to study renormalization. For a long time ithas been claimed" that renormalization does not removeinfinities from the Schrodinger equation, even in renor-malizable QFT. Only recently, the correct additional re-normalization was found by Symanzik in his rigorousconstruction of the Schrodinger representation. ' As ad-mitted by Symanzik, the proof of renormalizability israther of conceptual value, but uninviting to compute.The Lagrangian formulation is usually preferred becauseit maintains explicit Lorentz covariance and the discus-sion of renormalizability is more clear. The use of theLagrangian method is the main advantage of the OE un-der the variational method in Hamiltonian theory. TheOE possesses other advantages also, as it gives a sys-tematic approximation procedure and enables an easy ex-tension to finite temperature.

The Fermi theory is perturbatively nonrenormalizable,if n p 2. However, it has been pointed out that renormal-ization can be performed to the leading order of thelarge-N expansion, if n &4 (Refs. 3 and 13}. Moreover,renormalizability in n =2+a dimensions has been shownrigorously. ' In Sec. III we discuss the Fermi theory tothe first-order OE. To this approximation, renormaliza-tion can be explicitly performed, if only n &4. The resultis compared with the leading order of the 1/N expansion.In Sec. IV the finite-temperature behavior of the Fermitheory is studied in the same approximations. As con-cluded in Sec. V the renormalized theory appears trivialor precarious, depending on the choice of a bare couplingconstant. At a critical temperature the precarious theoryundergoes a phase transition to the massless noninteract-ing phase.

38 OPTIMIZED EXPANSION IN QUANTUM FIELD THEORY OF. . . 2509

ter, can be obtained using an implicit definition given by

Eqs. (1.3) and (1.4). Z [g,g]= JDQDgexp —( —S [g,P]+g'rl+~g)

A. Loop expansion

The conventional LE (Ref. 6) in Fermi theory can begenerated applying the steepest-descent method to thegenerating functional written in the form

(2.2)

Upon translating the integration variables and rescal-

ing them by A', the Planck constant can be used as theformal expansion parameter and we obtain

zion st='"P I ~(4 0 )1+0 9+ 94 ~ 'JD'SDS~*P~ —0G 'lfo 0 jDf+6+14~l&+ 0"(' '~I

=exp —( S[g—, g ]+/ rl+rlgo) Det(G '[P,P ])[1+0(A')], (2.3)

where the inverse fermion propagator in the background fields g and g is

2SG~a, [4 &»»]= — =(&~a&"+~~va [4 4]I(x»)

5$ 'z (x)5+&(y)

with mass matrix given by

(2.4)

MAa[4 1 ] m + PC0C 5Aa~ 1 A PBN N(2.5)

The determinant in Eq. (2.3}is taken with respect to space arguments and to discrete indices.The effective action to first order in A becomes

I [t/r, lntt]= f(j3+m—)f (Pf) —+Tr Ln(G '},2)V

and the effective potential can be written as

V (P, g) =—mfa+ (gg) f ln —det(/+M)1 — g —2 d "p

2N

(2.6}

(2.&)

B. Optimized expansion

In the calculation of the effective action we use a trick of Nambu and Jona-Lasinio, writing a classical action as

S.[4 4]=S [4 0]+ S [4 4]=0G 0+ 1('( —fI)4+ 2N(A') (2.8)

where the inverse fermion propagator is given by

GAa (x,y) —[8Aa +Q(x )5 Aa ]5(x,y) . (2.9)

The parameter e has been introduced to identify the order of the perturbation and is set equal to one at the end. In the

path integral (1.2) with the modified classical action (2.8) we translate integration variables to obtain a minimum of the

exponent. After expanding in e we obtain

Z[g, g]=exp —g G 'g att (m —Q)g + (—P P )2N

g2g{ 1) l g4g(1)p —o o + o —o o —o +Or

Sq'fiyo 4 nq'fiq'f y'fiq'

=exp Q„G„a/a e t}j „—(m —Q)g„+ (g—„g„) +rl „P„+g„g„Det G2N

X 1 —e N 0—m — g „P„Gaa—gg „G„ag„— (N G„„Gaa—NG„aGa„) +O(e )N 2N

(2.10)

2510 ANNA OKOPINSKA 38

The effective action to first order in e becomes

f'(tp, g, Q)= —p'A(8AB+m5AB)fa — (g'Ap'A ) +NTr Ln(G ') —N(Q —m)GBB+gp'AGBBQ'A2%

—gg'A GAB/'B — (N G„„GBB N—G„BGB„).2

2N(2.11)

The auxiliary field Q(x) has been introduced in such away that the generating functionals do not depend onthem. However, in the truncated series the dependenceappears. Using Stevenson s principle of minimal sensi-tivity, ' we make the kth-order approximant of theeffective action, as insensitive as possible to the smallvariation of 0, choosing 0 to satisfy

Here and in the following we use the notation

dnI, (Q)= —,

' f ln(p +Q )=f(277 )" (27r )'

I (Q)(2~)" p'+Q' (2n. )' 2~~

(2.16a)

(2.16b)

(2.12)

which can also be regarded as a requirement that thesources for the auxiliary field vanish. It would be possi-ble to improve the lowest-order approximation within thesame scheme, introducing more auxiliary fields in the ma-

trix O'Ja. For the simplest choice O'A~a =Q5'Js„a theeffective action is given by (2.11) with Q satisfying

g- g—(Q —m)G„BGB„—

N gA GAB GBA gA+ N QA GACGCBOB

+ (NGAAGBCGCB GABGBCGCA )gN

(2.13)

V(a, Q)=ma+ga dI, (Q)+[d (Q——m) —rga]QID(Q)

(2.14)+ rg [QI0—(Q)]

where r =(Nd —1)/N. The gap equation (2.13) turnsinto

Q m — ra+—grQIQ(Q) =—0, (2.15)

which is the same as obtained requiring BV/BO=O.

It is not possible to obtain a more explicit expression forthe effective action. However, this implicit expression en-ables us to calculate all derivatives of the effective actionwith respect to background fields g and g. When takenat /=/=0, they give 1PI vertices expressed in terms ofmomentum integrals.

The effective potential depends only on a=fP/N(which can be treated approximately as a real, positivenumber). To first order in e it becomes

((Q) =2 =, (2.16c)(2m)" (p +Q ) (2m. )" 2'

I(Q)= f "P ', =I,(Q) —Q'I, (Q), (2.16d)(2m. )" (p+Q)

where v=n —1 and co&——0 +p&+pz+ +p, . The

integrals Iz have been introduced in Ref. 10 with someuseful relation between the integrals Iz. In Table I we

quote the relations used in our work.In two-dimensional space-time the effective potential

given by Eq. (2.14) coincides (for m=O) with the Gauss-ian effective potential obtained in the Gross-Neveu modelby Latorre and Soto. They extended the variationalmethod for the functional Schrodinger equation in scalarQFT (Ref. 9) to Fermi fields, by taking delta trial vacuumfunctional. Our approach confirms their result and offersa possibility of systematically improving them.

For a=O our Eq. (2.15) coincides with the gap equa-tion obtained by Nambu and Jona-Lasinio, requiringthat radiative corrections to the self-energy vanish. Itcan be shown that their approach is equivalent to calcu-lating the two-particle vertex as a sum of perturbativeFeynman diagrams without overlapping divergences.Other vertices are calculated perturbatively with the useof the improved propagator. In our approach theeffective action is calculated as a sum of vacuum Feyn-man diagrams without overlapping divergences. The re-sult, which is renormalization-group invariant, is used toderive self-energy and other 1PI vertices. Only a self-energy taken at /=/=0 happens to be the same in bothapproacht:s; higher 1PI vertices differ. As will be seen inSec. III B the difference in the four-vertex is crucial forrenormaliz- ability —the (gP) QFT in three-dimensionalspace-time is renormalizable in the first-order OE, but

TABLE I. Relations between I~ integrals in n dimensions: x =Q /m&.

n =2 or 3

Il (Q) —I& (mq ) =—(Q —mz )Io(mz ) — m&L2(x)2 2 1

2 8~1

QIo{Q)—mRIo{ mq ) =(Q —mz )Io(mz ) — Qmq L, (x)4m

1/(2mQ ),„I-1(Q)—1/{4~Q), n 2

3S OPTIMIZED EXPANSION IN QUANTUM FIELD THEORY OF. . . 2511

not in the first order of the Nambu and Jona-Lasinio ap-proach.

In QFT of Fermi fields at finite temperature the in-

tegrals (1.6) should be replaced by (1.7), then the integralsgiven in Eqs. (2.16a) and (2.16b) turn into their finite-

temperature counterparts:

I, (Q)= —,'Tg f "ln(p +Q )

(2m )'

V (a, Q}=ma+ga d—I, (Q)

+ [d (Q —m) —rga]QID (Q)

+ —rg [QI[](Q)]

with 0 satisfying the gap equation

Q —m — ra—+gr QID (Q)=0,g T

(2.18)

(2.19)

d vp []]p —co /T+Tin 1+e(2m)

=I, (Q}+J,(Q},

I[](Q)=Tg f (2m)" p +Q

dvp 1 1 1

(2 }V i0 2 Cd /T

=I[](Q)+J[](Q) .

(2.17a)

(2.17b)

gi~es a finite-temperature Hartree approximation in QFT.

C. Mean-field theory

The mean-field (MF) expansion is obtained formallyby setting N equal to the number of fields in the given or-der of the large-N expansion, even if N is not large. Itcan be justified by a path-integral derivation of the expan-sion, when the role of 1/N as the formal parameter be-comes clear. Multiplying the generating functional (1.2)by a constant factor represented as

e

The temperature-dependent contributions J] (Q) and

Jo (Q ) are finite in any space dimensions v and vanish forT=0. The first-order optimized finite-temperatureeffective potential

C= fd8exp — 8—i m+N . g-2g N

(2.20)

and introducing a source S(») for an auxiliary field 8, thefunctional

mZ[q, q, S]=fD8exp — (8 2im 8)+—N fDQDgexp[ P(8 i8—)g+q—P+Pg+S8]

2g 2g

is defined. Integration over N fields P and g can be performed, leading to

[ , Z, C]C=c[fSDS exp( NF[9, CC, CCS]]—,

where

F[8,Ti, ri, S]=— + 8 — im8 ——TiGTi Tr—LnG ———S8m' 1 , 1. 1 , 1

2g 2g g N

and

(2.21)

(2.22)

(2.23)

G„B](»,y) = []c}„B i 8(»)5AB—]5(» —y) .

The steepest-descent method to the integral (2.22) gives a series in 1/N:

(2.24)

Z [g,g, S]=exp( NF [go, g, ri,—S])fD8exp —— 8 [1— (O1/ )N]=exp( N[F8 go, g, ]S+(O1/ )N} . (2.25)1 5F0

After replacing the sources by the background fields g, ]I(

given by Eq. (1.4) and Q= i 5 lnZ/5S, wi—th the aid of aLegendre transform the efFective action is obtained. Toleading order we have

r(y, y, Q}=N —'y(g+Q}y+ 'Q

'Qm

2g g

where

GAB(» y=}[]AB +Q(»}5AB ]5(»—y) (2.27)

In the physical theory the sources are absent, and thederivative of the effective action over 0 should vanish,leading to the gap equation

Q —m —g a+gd QIO(Q) =0, (2.28)Pl+Tr LnG2g

(2.26) where a=Pg/N and a consistency of the method re-quires Q)0. For constant fields the effective potential

2512 ANNA OKOPINSKA 38

can be expressed as mB™+g™o(m) (3.2)

2

V(a, Q)=Qa — Q +—Qm —dI, (Q)—2g

(2.29)

with Q given by Eq. (2.28).It is worthwhile to note that to the first order of the

OE the gap equation (2.15) for large N turns into (2.28)and the effective potential (2.14) reduces to (2.29) after us-

ing the gap equation. Similarly as for scalar fields, theGaussian effective potential in the large-N limit is exact.Therefore, for infinite N the leading-order MF and first-order OE give an exact result and for finite N bothmethods provide different approximation schemes. Theaccuracy of the approximations can be estimated by cal-culating higher-order contributions. The similarities ofthe MF and OE are due to the fact that in both methodsthe auxiliary field 0 includes some effects of compositefields. In the leading-order MF calculation of theeffective action the same class of perturbative Feynmandiagrams without overlapping divergences is summed, asin the first-order OE, only the coupling constant g is re-placed by gNd/(Nd —1), because only diagrams with acoupling between different fermions are included in MFand Pauli principle does not operate.

The finite-temperature effective potential to the leadingorder in 1/N is given by

2

V (a, Q)=Qa — Q + —Qm —dI, (Q)—,(2.31)&g

with 0 chosen to satisfy

and the renormalized coupling

gB=g 1 — g—r I(m)1

d(3.3)

Solving iteratively Eqs. (3.2) and (3.3) gives the bare mass

m =mB —grm„Io(mB )

and the bare coupling constant

(3.4)

1g =gB 1 — g—ar I(mB ) (3.5)

B. Renormalization in the optimized expansion

In the OE derivatives of the effective potential (2.14) ata =0 will be used as renormalized parameters Since 0as a function of a has been obtained requiring8 V/BQ=0, the first derivative of the effective potential issimply

Elimination of bare parameters with the aid of (3.4) and(3.5) removes all infinities from the effective potentialgiven by Eq. (2.7), only if the divergence of the integralI(mR ) in Eq. (3 ~ 5) is at most logarithmic. Therefore, ifthe space-time dimension is greater than two, the (gg)QFT appears nonrenormalizable already in the first orderof the LE.

Q —rn —ga+gd Q Io (Q) =0, (2.32) dV BV gada Ba

=m +ga grQIo(Q—) =Q+Nd

(3.6)

A. Renormalization in the loop expansion

The two-point proper vertex can be obtained as aFourier transform of the second derivative of the effectiveaction over renormalized fields. To the first order of theLE the renormalized self-energy becomes

I AB(p) Z[pAB+[m +grmIo(rn)]~AB1 . (3.1)

Renormalization is accomplished taking Z= 1, the renor-malized mass

III. RENORMALIZATION OF (QQ)2 GFT

The (PP) theory can be quantized in n-dimensionalspace-tine. If the dimension is greater than one, themomentum integrals in proper vertices become divergentand should be regularized, e.g. , with the help of UVcutoff A. The theory is renormalizable, if a finite and A-

independent content is obtained after reparametrizationin terms of renormalized fields 1(B ——Z' p, 1(R

——Zand physical quantities, instead of bare parameters. Inthis section we will compare the renormalization pro-cedure in different space-time dimensions to the lowestorder of the discussed expansions. The renormalizedmass and coupling are defined, as a second and fourthderivative of the effective potential at vanishing back-ground.

where the last equality has been obtained with the aid ofthe gap equation (2.15). This can be used to define the re-normalized mass by

dVma —— ——m grmBIo™—B ) .

dc'(3.7)

Taking into account that

dQ grda d [1+grI(Q)]

as found from the gap equation, we obtain

(3.8)

d V d=g 1 gr [QI(Q)]-dQda' dQ

1+(gr/Nd)I (Q)1+grI(Q)

and the renormalized coupling constant becomes

1+(gr/Nd)I(mB )=g

1+grI(m„)

(3.9)

(3.10)

Taking the effective action to the first-order OE (2.12)with Q given by (2.13) we find the renormalized two-point proper vertex at vanishing background fields equalto

1 »(p)=ZIp»+ [m grmBIo(mB )lfiwB] . —

38 OPTIMIZED EXPANSION IN QUANTUM FIELD THEORY OF. . . 2513

m =my +grmaIp(mg ) (3.12)

and

Therefore, taking mass-shell normalization conditions,we have Z=1 and the renormalized mass given by Eq.(3.7).

The effective potential to the first-order OE coincideswith the Gaussian effective potential, which renormaliza-tion in the two-dimensional case has been studied by La-torre and Soto for the massless theory. We can extendtheir analysis to an arbitrary bare mass and arbitraryspace-time dimension. Solving Eqs. (3.7) and (3.10) withrespect to bare parameters gives

1

rI(mR )

1

r dgR [I(mz )]

1 G

rIo(m„) r [Io(m„)]

with G defined by

G =mzI &(mz )+2 1

(3.15)

(3.16)

It is worthwhile to observe that requiring the baremass to vanish, as in the original Gross-Neveu model, re-quires the bare coupling g = —1/rIp(mz ), according toEq. (3.12). As can be seen from Eq. (3.15) it correspondsto G=O and Eq. (3.16) gives the renormalized coupling

Nd

2rI(ma )—1+garI(mz )

1

mR dI, (m„)

n=2,—2m /ma, n =3, (3.17)

0, n)4.+ 1+ g„I(ma )(2 —Nd)

Nd

2 21/2

+g, r [I(m„)] (3.13)

g =N dgz, (3.14)

or infinitesimal and negative:

If the dimension n & 2, the integral I(ma ) defined in Eq.(2.16d) diverges in the limit of an infinite cutoff. In thislimit the solutions (3.13) for g become finite

Therefore, fixing a bare mass to zero, fixes the renormal-ized coupling, while the dynamically generated mass m~remains arbitrary. That is unlikely with the scalar A,y"GFT (Refs. 10 and 5), when the relation between bareand renormalized mass is given by m =ma+12AIp(ma )

and although the bare coupling is vanishingly smallA. = —1/6I, (m~ ), the bare mass has to be infinite in or-der to have finite renormalized parameters.

In two- and three-dimensional space-time the Diracspinor has d =2 components; therefore, the effective po-tential is very similar. After eliminating the bare massand adding an infinite-constant term the effective poten-tial can be written as

V(a Q) =ma a+ga 2[I&(Q) I& (ma )]+2(Q—ma )QIp(Q) rga[QIp(Q) mgIp(mg )]

+gr [QIo(Q) —m&Ip(mz )]

and the gap equation turns into

Q —ma ——ra+gr[QIo(Q) —maIo(ma )]=0 .g2

With the relations of Table I, the effective potential becomes

(3.18)

(3.19)

V(a, Q) ™~a+ga—(Q —mR )Io(ma )+ maL2(x)+2(Q —m„)QIo(Q)4a

1 1+rga Qmg L, (x)—(Q —ma )Io(ma ) +rg Qma L, (x)—(Q —m~ )Ip(m„)

4m. 4~

2

(3.20)

and the gap equation can be written as

fL —mg — r A2

1gr Qmg L&(x—) —(Q —mg )Ip(mg ) =0,4'

where x =0 /mz and the functions L,- are different intwo- and three-dimensional space-time, as given in TableII.

It remains to eliminate the bare coupling constant. Ifwe take it to be finite g =2Ng~, the gap equations can besatisfied with finite 0, only if

a=2(Q —m~ )Io(m~ ) (3.22)

(3.21) and after eliminating Q the effective potential becomes

2514 ANNA OKOPINSKA 38

TABLE II. The L, (x) functions used in relations given in

Table I.and

m]] ——m —gdm]]IO(mR ) (3.29)

n =even

L, (x)= ln(x)L (x)=x ln(x) —(x —1)

n =odd

Ll (x)=(&x —1)L (x)=—'(&x —1) (2&x + 1)

1+g dI(mR )(3.30)

finite:

V(a ) =m]] a+ —,'g]]a (3.23)

From the leading-order expression for the effective action(2.26) we find the renormalized two-point proper vertexfor a vanishing background to be equal:

I (p)=Z[p„z+[m —gdmzIO(mz)]5„&] . (3.31)

In this case the finite-temperature effective potential,after using the gap equation becomes

Therefore, with Z=1 and m]] given by Eq. (3.29), themass-shell renormalization is accomplished. Hence, thebare mass has to be chosen as

V (a)=m]]a+ —,'g]]a —2J, (mR ) . (3.24)m =m]t+g dm]]IO(m~ ) . (3.32)

The first-order effective potential suggests that the renor-malized theory differs only in replacing bare parametersby renormalized ones. However, the finite-temperaturebehavior indicates that the theory is noninteracting, asthe temperature contribution does not depend on thebackground fields and is the same as for free particle witha mass ply.

If the infinitesimal solution (3.15) for the bare couplingconstant is taken, the precarious effective potential

a+ Qm]] 'L, (x)—26(Q ms)=—0.2' (3.26)

V(a)=aQ+ mgL2(x) G(Q —mz)—4a

is finite for all Q. Requiring dVldQ=O, gives the gapequation

Keeping the bare coupling constant g nonvanishing, thegap equation (2.28) can be satisfied with finite Q, only if

a=2(Q —m]] )Io(m]] ) . (3.33)

V(a) =m~a,

and the finite-temperature effective potential

V (a)=m]ta —2J] (m„)

(3.34)

(3.35)

is a free energy of the free particle with a mass mz.The other possibility is to choose the bare coupling

constant as the infinitesimal solution of Eq. (3.30):

In this case the renormalized coupling constant ap-proaches zero and after eliminating 0 the effective poten-tial becomes trivial,

At finite temperature the renormalized effective potentialto the first-order OE is given by

V (a) =aQ+ m„"L2(x)—G(Q —m]] ) —2J, (Q),4m.

(3.27)

where 0 satisfies

gR

1 gRdr™R)—which in the limit of the infinite cutoff becomes

1 6dIO(m]] ) d [Io(m]] )]

(3.36)

(3.37)

with G defined by (3.16). In two- and three-dimensionalspace-time, after eliminating the bare parameters withthe aid of (3.32) and (3.37), the same precarious theory asin the OE is obtained; the finite-temperature effective po-tential is given by (3.27) with Q satisfying (3.28). If thedimension of space-time is greater than or equal to four,the theory appears nonrenormalizable in the leading or-der MF.

It is worthwhile to mention that similar features havebeen found in A, ])t] theory in four dimensions, studied insimilar approximations at zero' and finite tempera-ture, ' ' and they persist in five dimensions.

a+ Qm„" L, (x) —26(Q —m]] ) —2QJO(Q)=0 .2'(3.28)

For T=O, the temperature-dependent contributions van-ish and the result turns into a precarious effective poten-tial (3.25).

In the (Pg) theory in four- and greater-dimensionalspace-time it can be found by inspection that eliminationof the bare parameters with the aid of renorrnalized onesdoes not remove infinities from the effective potential foreither choice of bare coupling, since the integral I &(0)diverges.

C. Renormalization in the mean-field expansion

In the MF approximation the renormalized mass andcoupling constant defined by the first and second deriva-tives of the effective potential are equal:

IU. FINITE-TEMPERATURE BEHAVIOROF ( tPQ) QFf IN TWO AND THREE DIMENSIONS

As discussed in the previous section, renormalizationof the QFT with (PP) interaction can be performed inthe leading order of the MF expansion, as well as in thefirst order of the OE, if the space-time dimension is less

38 OPTIMIZED EXPANSION IN QUANTUM FIELD THEORY OF. . . 2515

than four. However, the only possibility to obtain non-trivial renormalized theory is to choose the bare couplinginfinitesimal negative, which gives the same precarioustheory in both approximations. In this section we willdiscuss numerical results in two- and three-dimensionalspace-time. For arbitrary bare mass, the renormalizedtheory can be parametrized by mR and gR. The masslessGross-Neveu model will be recovered for gR given by(3.17). To get rid of one parameter we express all dimen-sional quantities in units of an arbitrary mR.

It is necessary to stress that our analysis is limited tothe lowest order of the considered expansions. In two di-

mensions, when the perturbative proof of renormalizabili-ty exist, it provides an approximation of the renormalizedtheory. However, in three dimensions the results can ap-pear meaningless, if renormalizability of the theorywould not be maintained in higher orders.

A. Precarious theory in two dimensions

In two-dimensional QFT the precarious finite-temperature efFective potential (3.27), after taking thefunctions L; from Table II (n even), becomes

V (a)=aQ+ Q ln(Q) — (Q —1)—G(Q —1) —2—f dp ln(l+e ' +~ ' ~)2' 4m ~ 0

with Q determined by the gap equation (3.28), which becomes

(4.1)

a+ —Q ln(Q) —26(Q —1)+—1

(Q +p )'~~texp[(Q +p )'~ /T]+I)=0, (4.2)

where

1 1 16 ———+2 7T gR

(4.3)

For T =0 the gap equation (4.2) has a solution only for

a &a,„=—e " —26= —e2~G —&

7T 7r gR(4.4)

Therefore the range in which the precarious effective po-tential is determined in the discussed approximation isfinite and a,„~ec, when ~ga ~

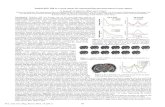
~0. For fixed renor-malized coupling constant a,„decreases with increasingtemperature. The critical temperature T„ is that atwhich a,„=O; i.e., the gap equation has a solution onlyfor a =0. We will study the case 6 =0 as an example. InFig. 1 we show the effective potential at T=0 and

T =0.3. The zero-temperature result coincides with thatobtained by Latorre and Soto. The critical temperatureis T„=(lie)er =0.567 (y=0. 577. . . is Euler's con-stant), which agrees with the value obtained in the paperson the thermal behavior of the Gross-Neveu model in theleading order of the 1/N expansion, ' although their dis-cussion has been done in a different way —studying thefinite-temperature effective potential for a compositefield. The phase transition is of the second order becausethe second derivative of the effective potential, whichplays a role of the order parameter, decreases smoothlywith increasing temperature and approaches zero at T„.That is unlikely with A,P theory, where the order paratn-eter jumps from a finite value to zero at critical tempera-ture, because the value of the finite-temperature effectivepotential at the end point Q=O becomes lower than thevalue obtained using the gap equation. '

V

0.03—

0.05

0.05 0.14

0.05

FICy. l. The effective potential for (gg) QFT in two-dimensional space-time at T =0 and T =0.3. The critical tem-perature T,„=0.567. All variables are in the units of renormal-ized mass m&.

FIG. 2. The effective potential for (fP) QFT in three-dimensional space-time at T =0 and T =0.4. The critical tem-perature T„=0.721. All variables are in the units of renormal-ized mass m~.

2516 ANNA OKOPINSKA 38

B. Precarious theory in three dimensionsV (a)=aQ+ (0—1) (20+1)—6(Q —1)

12m

The precarious finite-temperature effective potential inthree-dimensional QFT, after taking the functions L,from Table II (n odd), becomes

1+e—(0 +P ) /T77 0

with the gap equation given by

a+ Q(Q —1)—26(Q —1)+-2m. tr o (0'+p')'~'[exp[(Q'+p')' 'T]+ 1 t

(0—1)—26(A —1)+ ln(1+e ) =0 .2' 2' (4.6)

These equations are simpler than in the two-dimensionalcase. For zero temperature the gap equation is quadraticwith two solutions:

0—= —,'

I 1 +4m G+[(1—4n 6 ) —8na]'izI (4.7)

and the corresponding branches of the effective potential

V —=—+ —— [( 1 —4~6 ) 8na] —+.ct cx 1

2 3 24m 24~

(4.8)

are defined for

tt &a,„= (1—4m.G ) =1 p vr

2gR

Therefore, a,„ increases infinitely when~ ga ~

~0. Thedependence on the temperature is also similar to thetwo-dimensional case; i.e., a,„decreases with increasingtemperature. For G =0 the effective potential at T =0and T=0.4 is shown in Fig. 2. In this case, the criticaltemperature T„=1/2 ln2=0. 721 and the transition is ofsecond order.

coupling constant g.If g is finite, the theory is noninteracting. In the MF

method the triviality of the theory can be seen from thebehavior of the effective potential. In the OE consideringthermal properties is necessary to draw this conclusion.

If g is chosen to be infinitesimally negative, the theoryappears precarious. The renormalized effective potentialcoincides with that obtained in the MF approximation,although the unrenormalized results are different. Thefinite-temperature behavior of the precarious theory sug-gests a second-order phase transition to a free theory ofmassless particle. However, it should be stressed that theconclusion is drawn using the end-point behavior of thefinite-temperature eff'ective potential when the OE, aswell as the MF, are unreliable. The lack of a solution tothe gap equation can be only a signal that both methodsbreak down beyond a critical temperature.

Note added. For finite temperature similar results havebeen deduced' from the Gaussian effective potential cal-culated in compact space (S'), using an analogy betweeninternal energy in the space with closed dimension andthe free energy in Minkowski space.

V. CONCLUSIONS ACKNOWLEDGMENTS

The results of the study of the QFT of Fermi fieldswith a (gtj'r) interaction to the first order of the OE arevery similar to those obtained in the leading order of theMF expansion. The theory can be renormalized, if thespace-time dimension is less than four, but the result istrivial or precarious, depending on the choice of the bare

The author wishes to acknowledge M. Spalinski and R.Tarrach for reading the manuscript. Thanks are alsogiven to M. W. Kalinowski for several comments. Thiswork was supported in part by the Polish Ministry of Sci-ence and Higher Education under Contract No. CPBP01.03.

'W. Heisenberg, Introduction to the Uni+ed Field Theory of Elementary Particles (Interscience, London, 1966). Earlier pa-pers are quoted there.

2Y. Nambu and G. Jona-Lasinio, Phys. Rev. 122, 345 (1960).3D. J. Gross and A. Neveu, Phys. Rev. D 10, 3235 (1974).~J. I. Latorre and J. Soto, Phys. Rev. D 34, 3111 (1986).sA. Okopinska, in Proceedings of the VIII 8'arsaw Symposium

on Elementary Particle Physics, Kazimierz, Poland, 1985,edited by Z. Ajduk (Institute of Theoretical Physics, Warsaw,1985); Phys. Rev. D 35, 1835 (1987).

R. Jackiw, Phys. Rev. D 9, 1686 (1974).7L. Dolan and R. Jackiw, Phys. Rev. D 9, 3320 (1974).8F. Cooper, G. S. Guralnik, and S. H. Kasdan, Phys. Rev. D 14,

1607 ()976); C. M. Bender, F. Cooper, and G. S. Guralnik,Ann. Phys. (N.Y.) 109, 165 (1977).

9J. M. Cornwall, R. Jackiw, and E. Tomboulis, Phys. Rev. D 10,2428 (1974); T. Barnes and G. I. Ghandour, ibid. 22, 924(1980).P. M. Stevenson, Phys. Rev. D 32, 1389 (1985).N. N. Bogoliubov and D. V. Shirkov, Introduction to the

38 OPTIMIZED EXPANSION IN QUANTUM FIELD THEORY OF. . . 2517

Theory of Quantized Fields (Wiley-interscience, New York,1979).

t2K. Symanzik, Nncl. Phys. B190 [FS3], 1 (1981).' K. Wilson, Phys. Rev. D 7, 2911 (1973);G. Parisi, Nucl. Phys.

B100, 368 (1975).K. Gawedzki and A. Kupiainen, Phys. Rev. Lett. 55, 363(1985);Nucl. Phys. B262, 33 (1985).

' P. M. Stevenson, Phys. Rev. D 23, 2916 (1981).W. A. Bardeen and M. Moshe, Phys. Rev. D 28, 1382 (1983);

34, 1229 (1986).' I. Roditi, Phys. Lett. 169B, 264 (1986); A. Okopinska, Phys.

Rev. D 36, 2415 (1987).' H. O. Wada, Lett. Nuovo Cimento 1I, 697 (1974); L. Jacobs,

Phys. Rev. D 10, 3956 (1975); B.J. Harrington and A. Yildiz,ibid. 11, 779 (1975); R. F. Dashen, S. Ma, and R. Rajaraman,ibid. 11, 1499 (1975).J. Soto, Phys. Rev. D 37, 1086 (1988).