Damped Oscillations
description
Transcript of Damped Oscillations

Physics 1D03 - Lecture 35 1
Damped Oscillations
(Serway 15.6-15.7)

Physics 1D03 - Lecture 35 2
Simple Pendulum
L
θ T
Lg
dtd
2
2
mg
Recall, for a simple pendulum we have thefollowing equation of motion:
Which give us:Lg
Hence:2
2
2 4gTgL
Application - measuring height - finding variations in g → underground resources
or: 2
22 4
TLLg
-------------------------------------------------------------------------

Physics 1D03 - Lecture 35 3
t
x
x
t
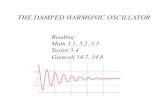
SHM: x(t) = A cos ωt Motion continues indefinitely. Only conservative forces act, so the mechanical energy is constant.
Damped oscillator: dissipative forces (friction, air resistance, etc.) remove energy from the oscillator, and the amplitude decreases with time.
SHM and Damping

Physics 1D03 - Lecture 35 4
)cos()( 2
tAetxt
mb
For weak damping (small b), the solution is:
f = bv where b is a constant damping coefficient
x
t
A damped oscillator has external nonconservativeforce(s) acting on the system. A common example is a force that is proportional to the velocity.
eg: green water(weak damping)
A e-(b/2m)t
2
2
dtxdm
dtdxbkx F=ma give:

Physics 1D03 - Lecture 35 5
Without damping: the angular frequency is
22
0
2
22
mb
mb
mk
the amplitude gets smaller (decays exponentially) as time goes on:
mk0
With damping:
tmb
oeAtA 2)(
Effectively, the frequency ω is slower with damping, and

Physics 1D03 - Lecture 35 6
Example: A mass on a spring oscillates with initial amplitude 10 cm. After 10 seconds, the amplitude is 5 cm.
Question: What is the amplitude after 30 seconds?
Question: What is the value of b/(2m)?

Physics 1D03 - Lecture 35 7
Example: A pendulum of length 1.0 m has an initial amplitude 10°, but after a time of1000 s it is reduced to 5°. What is b/(2m)?

Physics 1D03 - Lecture 35 8
220 2
mb
water
axle grease?
Eg: Strong damping (b large): there is no oscillation when:
02
mb
Types of Damping
Since:
We can have different cases for the value underthe root: >0, 0 or <0. This leads to three types ofdamping !

Physics 1D03 - Lecture 35 9
02 mb
x(t)
t
overdamped
critical damping
underdamped
: “Overdamped”, no oscillation
: “Underdamped”, oscillations with decreasing amplitude
: “Critically damped”
Critical damping provides the fastest dissipation of energy.
02 mb
02 mb

Physics 1D03 - Lecture 35 10
Quiz: If you were designing a automobile suspensions:
Should they be:
a) Underdamped
b) Critically damped
c) Overdamped
d) I don’t need suspension !

Physics 1D03 - Lecture 35 11
Example:
Show that the time rate of change of mechanical energy for a damped oscillator is given by:
dE/dt=-bv2
and hence is always negative.

Physics 1D03 - Lecture 35 12
Damped Oscillations and Resonance
(Serway 15.6-15.7)
• Forced Oscillations• Resonance

Physics 1D03 - Lecture 35 13
Forced Oscillations
A periodic, external force pushes on the mass(in addition to the spring and damping):
tFtFext cos)( max
The frequency is set by the machine applying the force. The system responds by oscillating at the same frequency . The amplitude can be very large if the external driving frequency is close to the “natural” frequency of the oscillator.
This transfers energy into the system

Physics 1D03 - Lecture 35 14
is called the natural frequency or resonant frequency of the oscillation.m
k0
2
2
max cosdt
xdmdtdxbkxtFF
2
220
2
max
mb
mF
A
Newton’s 2nd Law:
Assume that : x = A cos (t + ) ; then the amplitude of a drive oscillator is given by:

Physics 1D03 - Lecture 35 15
So, as the amplitude, A, increases !
If the external “push” has the same frequency as the resonant frequency ω0. The driving force is said to be in resonance with the system.
0
0
A
2
220
2
max
mb
mF
A

Physics 1D03 - Lecture 35 16
Resonance occurs because the driving force changes direction at just the same rate as the “natural” oscillation would reverse direction, so the driving force reinforces the natural oscillation on every cycle.
Quiz: Where in the cycle should the driving force be at its maximum value for maximum average power?
A) When the mass is at maximum x (displacement)
B) When the mass is at the midpoint (x = 0)
C) It matters not

Physics 1D03 - Lecture 35 17
Example
A 2.0 kg object attached to a spring moves without friction and is driven by an external force given by:
F=(3.0N)sin(8πt)
If the force constant of the spring is 20.0N/m, determine
a) the period of the motion
b) the amplitude of the motion

Physics 1D03 - Lecture 35 18

Physics 1D03 - Lecture 35 19
Summary
• An oscillator driven by an external periodic force will oscillate with an amplitude that depends on the driving frequency. The amplitude is large when the driving frequency is close to the “natural” frequency of the oscillator.
•For weak damping, the system oscillates, and the amplitude decreases exponentially with time.• With sufficiently strong damping, the system returns smoothly to equilibrium without oscillation.