Chapter 8 Rotation of Rigid Body -...

CHAPTER 8 ROTATION OF RIGID BODY prepared by Yew Sze Ling@Fiona, KML

1

Chapter 8 Rotation of Rigid Body

Curriculum Specification Remarks

Before After Revision

8.1 Rotational Kinematics

a) Define and use

i. Angular displacement, θ

ii. Average angular velocity, ωav

iii. Instantaneous angular velocity, ω

iv. Average angular acceleration, αav

v. Instantaneous angular acceleration, α

(C1, C2, C3, C4)

b) Relate parameters in rotational motion with their

corresponding quantities in linear motion:

𝑠 = 𝑟𝜃, 𝑣 = 𝑟𝜔, 𝑎𝑡 = 𝑟𝛼,

(C1, C2, C3, C4)

c) Solve problem related to rotational motion with constant

angular acceleration.

𝜔 = 𝜔𝑜 + 𝛼𝑡, 𝜃 = 𝜔𝑜𝑡 +1

2𝛼𝑡2 and 𝜔2 = 𝜔𝑜

2 + 2𝛼𝜃

(C3, C4)

8.2 Equilibrium of a Uniform Rigid Body

a) Define torque, 𝜏 = 𝑟 × �⃗�. (C1, C2)

b) Solve problems related to equilibrium of a uniform rigid

body. (C3, C4)

8.3 Rotational Dynamics

a) Define and use the moment of inertia of a uniform rigid

body (sphere, cylinder, ring, disc, and rod). (C1, C2)

b) Determine the moment of inertia of a flywheel.

(Experiment 4: Rotational motion of rigid body)

(C1, C2, C3, C4)

c) State and use torque, 𝜏 = 𝐼𝛼. (C1, C2, C3, C4)

8.4 Conservation of Angular Momentum

a) Define and use angular momentum, 𝐿 = 𝐼𝜔.

(C1, C2, C3, C4)

b) State and use principle of conservation of angular

momentum. (C1, C2, C3, C4)

𝑎𝑐 = 𝑟𝜔2 =𝑣2

𝑟


2

8.1 Rotational Kinematics

A rigid object is an object with a definite shape that doesn’t

change, so that the particles composing it stay in fixed positions relative to one another.

The motion of a rigid object can be analysed as the translational

motion of the object’s centre of mass, plus rotational motion

about its centre of mass.

In the simplest kind of rotation, points on a rigid object move on circular paths. The centres of all such circular paths define a line, called the axis of rotation.

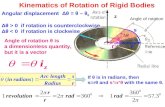
Angular displacement

When a rigid body rotates about a fixed axis, the angular displacement is the angle ∆θ swept out

by a line passing through any point on the body and intersecting the axis of rotation perpendicularly.

S.I. unit: rad (radian)

Other unit:

o Revolution (rev) → 1 rev = 2π rad

o Degree (°) → 360° = 2π rad

Sign convention:

o Negative → if the rotational motion is clockwise

o Positive → if the rotational motion is anticlockwise

Average angular velocity

The average angular velocity is defined as the angular displacement ∆θ divided by the elapsed time ∆t during which the displacement occurs.

S.I. unit: rad s-1

Other unit:

o Revolution per second (rps) → 1 rps = 2π rad s-1

o Revolution per minute (rpm) → 1 rpm = 2𝜋

60 rad s

-1

Direction:

Rotational

Translational

�̅� =𝜃𝑓 − 𝜃𝑖𝑡𝑓 − 𝑡𝑖

=∆𝜃

∆𝑡


3

Instantaneous angular velocity

The instantaneous angular velocity ω is the angular velocity that exists at any given instant.

Commonly referred as ‘angular velocity at point A’ or ‘angular velocity at time t ’

All points in a rigid object rotate with the same angular velocity, since every position in the

object moves through the same angle in the same time interval.

Average angular acceleration

The average angular acceleration is defined as the change in angular velocity ∆ω divided by the elapsed time ∆t.

S.I. unit: rad s-2

Direction:

Sign convention

o Positive → if the angular velocity is increasing

o Negative → if the angular velocity is decreasing

Instantaneous angular acceleration

The instantaneous angular acceleration α is the angular acceleration at a given instant.

Commonly referred as ‘angular acceleration at point A’ or ‘angular acceleration at time t ’

Since is the same for all points of a rotating object, α also will be the same for all points.

𝜔 = lim∆𝑡→0

∆𝜃

∆𝑡=𝑑𝜃

𝑑𝑡

�̅� =𝜔𝑓 − 𝜔𝑖

𝑡𝑓 − 𝑡𝑖 =

∆𝜔

∆𝑡

𝛼 = lim∆𝑡→0

∆𝜔

∆𝑡=𝑑𝜔

𝑑𝑡


4

Relation between Rotational and Linear Motion

When a rigid body rotates about a fixed axis, all the particles in the

rigid body move in a circular path. Since the particle moves through

a distance s on a circular arc of radius r :

The magnitude of the tangential speed at point P is 𝑣 =𝑑𝑠

𝑑𝑡, where s

is the distance travelled by point P along the circular path. Recalling

𝑠 = 𝑟𝜃, where r is constant, we obtain

Since 𝑑𝜃

𝑑𝑡= 𝜔, thus

When a rigid body rotates about an axis at angular velocity ω,

different points on the body moves at different linear velocity, v.

Since, r2 > r1 → v2 > v1

We can relate the angular acceleration of the rotating rigid object to the tangential acceleration of the point P by taking the time derivative of v:

Since 𝑑𝜔

𝑑𝑡= 𝛼, thus

In chapter 6, we found that a point moving in a circular path undergoes a radial acceleration directed toward the centre of rotation and whose magnitude is that of the centripetal acceleration:

Thus, the total acceleration at point P is �⃗⃗⃗� = 𝒂𝒕⃗⃗⃗⃗⃗ + 𝒂𝒄⃗⃗⃗⃗⃗

Magnitude of total acceleration at point P:

Direction of total acceleration:

𝑠 = 𝑟𝜃

𝑣 =𝑑𝑠

𝑑𝑡 = 𝑟

𝑑𝜃

𝑑𝑡

𝑣 = 𝑟𝜔

𝑎𝑡 =𝑑𝑣

𝑑𝑡 = 𝑟

𝑑𝜔

𝑑𝑡

𝑎𝑡 = 𝑟𝛼

𝑎𝑐 =𝑣2

𝑟= 𝑟𝜔2

𝑎 = √𝑎𝑡 + 𝑎𝑐

tan 𝜃 =𝑎𝑡𝑎𝑐


5

The symbols used in linear and rotational kinematics:

The analogy of linear motion with rotational motion parameters:

8.2 Equilibrium of a Uniform Rigid Body

We know that net external force acting on an object causes linear motion to change, but what causes rotational motion to change?

The tendency of a force to rotate an object about some axis is measured by a quantity called

torque.

The magnitude of torque is defined as the magnitude of force times the lever arm:

The line of action is an extended line drawn collinear with the

force.

The lever arm d (or moment arm) is the distance between the

line of action and the axis of rotation, measured on a line that is

perpendicular to both.

𝜏 = 𝐹𝑑 = 𝐹𝑟 sin 𝜃

𝑟 × �⃗�


6

Force acting at different angles/positions at the door

τ = Fd = Fr sin 90° τ = 0 because d = 0, since line of action passes through axis

S.I. unit: Newton-meter (N m)

Sign convention:

o Negative → if the rotational motion is clockwise

o Positive → if the rotational motion is anticlockwise

Torque is a vector.

Direction:

8.3 Rotational Dynamics

Torque (Equilibrium)

A rigid body is in equilibrium if it has zero translational acceleration and zero angular

acceleration.

In equilibrium, the sum of the externally applied forces is zero, and the sum of the externally

applied torques is zero:

Centre of Gravity

The centre of gravity of a rigid body is the point at which its weight can be considered to act when the torque due to the weight is being calculated.

If you point the fingers of

your right hand in the

direction of r and then curl

them in the direction of F,

your outstretched thumb

points in the direction of τ.

∑𝐹𝑥 = 0 ∑𝜏 = 0 ∑𝐹𝑦 = 0


7

Torque (Rotational Dynamics)

For particle m1:

For particle m2:

All particles have the same angular acceleration since the rotating object is assumed to be rigid.

For N amount of particles in a rigid body,

For the rotation of a rigid object about a fixed axis, the nett torque acting on the rigid body is proportional to the body’s angular acceleration.

That is analogous to the nett force,

Moment of Inertia

Moment of inertia is defined as the sum of the products of the mass of each particle and the square of its respective distance from the rotation axis.

I (rotational) is analogous to the mass, m (linear).

𝜏1 = 𝐹1𝑟1 sin 90 °

𝜏1 = (𝑚1𝑎1)𝑟1

𝜏1 = [𝑚1(𝑟1𝛼1)]𝑟1

𝜏1 = 𝑚1𝑟12𝛼1

𝜏2 = 𝑚2𝑟22𝛼2

I1, moment of inertia of particle m1

I2, moment of inertia of particle m2

𝛼1 = 𝛼2 = 𝛼𝑁 = 𝛼

∑𝜏 = (∑𝑚𝑖

𝑁

𝑖=1

𝑟𝑖2)𝛼

I, moment of inertia of rigid body

∑ 𝜏 = 𝐼 𝛼

∑𝐹 = 𝑚𝑎

𝐼 = ∑𝑚𝑖

𝑁

𝑖=1

𝑟𝑖 2


8

The moments of inertia for a number of objects about axes through the centre of mass:

8.4 Conservation of Angular Momentum

The angular momentum L of a body rotating about a fixed axis is the product of the body’s

moment of inertia I and its angular velocity ω with respect to that axis:

S.I. unit: kg m s-2

Direction:

The Principle of Conservation of Angular Momentum

The total angular momentum of a system remains constant (is conserved) if the net average external

torque acting on the system is zero.

𝐿 = 𝐼 𝜔

𝐿 = 𝐼𝜔 = constant if the ∑ 𝜏 = 0

∑ 𝐿initial =∑ 𝐿 final


9

Example

Summary


10

Exercise

Rotational Kinematics

1. A gymnast on a high bar swings through two revolutions in a time of 1.90 s. Find the average

angular velocity (in rad s-1

) of the gymnast.

Answer: 6.61 rad s-1

2. If a disc 30 cm in diameter rolls 65 m along a straight line without slipping, calculate,

a) the number of revolutions would it makes in the process b) the angular displacement would be through by a speck of gum on its rim

Answer: 69 rev; 138π rad

3. A flywheel has a constant angular deceleration of 2.0 rad s–2

.

a) Find the angle through which the flywheel turns as it comes to rest from an angular

velocity of 220 rad s–1

b) Find the time required for the flywheel to come to rest

Answer: 12100 rad; 110 s

Equilibrium of a Uniform Rigid Body

1. Determine a resultant torque of all the forces

about rotation axis, O in the following problems.

Answer: − 40 N m (clockwise)

2. A cat walks along a uniform plank that is 4.0

m long and has a mass of 7 kg. The plank is

supported by 2 sawhorses one 0.5 m from the

left end of the board and other 1.50 m from its

right end. When the cat reaches the right end,

the plank just begins to tip. What is the mass of the cat?

Answer: 2.33 kg

3. A traffic light hangs from a structure as shown above.

The uniform aluminium pole AB is 7.5 m long has a

mass of 8.0 kg. The mass of the traffic light is 12.0 kg. Determine,

a) the tension in the horizontal massless cable CD

b) the vertical and horizontal components of the

force exerted by the pivot A on the aluminium pole

Answer: 248 N; 197 N, 248 N


11

Rotational Dynamics

1. An object of mass 1.50 kg is suspended from a rough pulley of radius

20.0 cm by light string as shown. The pulley has a moment of inertia

0.020 kg m2 about the axis of the pulley. The object is released from rest

and the pulley rotates without encountering frictional force. Assume that

the string does not slip on the pulley. After 0.3 s, determine,

a) the linear acceleration of the object,

b) the angular acceleration of the pulley,

c) the tension in the string,

d) the linear velocity of the object, e) the distance travelled by the object.

Answer: 7.36 m s-2

; 36.8 rad s-2

; 3.68 N; 2.21 m s-1

; 0.331 m

2. A 5.00 kg object placed on a frictionless horizontal table is

connected to a string that passes over a pulley and then is

fastened to a hanging 9.00 kg object as in Figure. The pulley has

a radius of 0.250 m and moment of inertia I. The block on the

table is moving with a constant acceleration of 2.00 m s-2

.

a) Calculate T1 and T2 the tensions in the string. b) Determine I.

Answer: 10.0 N, 70.3 N; 1.88 kg m2

Conservation of Angular Momentum

1. A light rigid rod 1.0 m in length rotates in the xy plane about a

pivot through the rod’s centre. 2 particles of masses 4 kg and

3 kg are connected to its end. Determine the angular momentum

of the system about the origin at the instant the speed of each particle is 5.0 m s

–1. ( Neglect the mass of light rod )

Answer: 17.5 kg m2 s

-1

2. A horizontal disc rotates about an axis which passes vertically through the centre of the disc

with angular velocity of 100 rpm. A small particle of mass 10 g is dropped onto the disc 9.0

cm from the axis and sticks to the disc. If the angular velocity is reduced to 90 rpm,

determine the moment of inertia of the disc about the axis.

Answer: 7.3×104 kg m

2

Chapter 8 Rotation of Rigid Body -...

Documents

Transcript of Chapter 8 Rotation of Rigid Body -...