Z y x θ φ |ψ>|ψ> z y x θ φ |ψ>|ψ> Quantum Computing presented by Scott Erholm and Bob Wall.
-
date post
21-Dec-2015 -
Category
Documents
-
view
237 -
download
0
Transcript of Z y x θ φ |ψ>|ψ> z y x θ φ |ψ>|ψ> Quantum Computing presented by Scott Erholm and Bob Wall.

z
y
θ
φ
|ψ>z
y
θ
φ
|ψ>
Quantum Computingpresented by
Scott Erholm and Bob Wall

z
y
θ
φ
|ψ>
Motivation for Quantum Computing
•Moore's Law: The number of transistors capable of being
placed
on a chip doubles every 18 months.
•If the number or transistors doubles, then individual size
must decrease, or we would have gigantic processors which
would require enormous amounts of energy and
generate destructive heat.
•Therefore, size must decrease as complexity increases.
•Intel's latest technique uses a 90nm process.
•Each transistor is 50nm wide.
•Some gates are a scant 1.2nm wide.
•1.2nm is the same width as about 5 silicon atoms

z
y
θ
φ
|ψ>
Nu
mb
er
of
Ato
ms
per
Bit
The number of atoms needed to represent one bit has been decreasing
nearly linearly. Extrapolation suggests the one-atom-per-bit level would
be reached in in about 2020.
Before then, we will either hit a wall and fail to keep up with Moore's pace,
or we will be forced to use and exploit quantum effects in computers.

z
y
θ
φ
|ψ>
Brief History of Quantum Computing
•1982 Richard Feynman proposes quantum computer
•1985 David Deutsch gives a description of a universal quantum computer
•Pre-1994 Quantum computing remains a marginal curiosity
•1994 Peter Shor introduces quantum algorithm for factoring integers and
extracting discrete logarithms in polynomial time
•1995 Shor establishes theory of quantum error-correcting codes
•1997 Ethan Bernstein and Umesh Vazirani construct theoretical quantum
Turing machine
•1998 First working 2-qubit NMR demonstrated at Berkeley.
•1999 First working 3-qubit NMR demonstrated at IBM
•2000 First working 5-qubit NMR demonstrated at IBM
•2001 First working 7-qubit NMR demonstrated at IBM
•2004 “Flying Qubit” is demonstrated by researchers at U. Michigan

z
y
θ
φ
|ψ>
In normal, or “classical” computing, the basic unit of information is the bit➢A bit can be in one of two states, 0 or 1
Representing quantum information
In quantum computing, the basic unit of information is the “qubit”➢After measurement, a qubit will be in one of two states, |0> or |1>
➢|0>, |1> notation called “ket”, invented by Dirac➢States of a qubit can be represented by entities which resolve two
states, such as:➢Photon: Vertical or Horizontal polarization➢Electron: Spin up or Spin down➢Atom: Discrete energy levels
➢|0> and |1> are called “basis states”➢Prior to measurement however, the qubit exists in some linear
combination of states:
|ψ> = α|0> + β|1>
which is called a superposition.

z
y
θ
φ
|ψ>
Superposition |ψ> = α|0> + β|1>
α and β coefficients are complex numbers, called the amplitudes of
superposition
α = x0 + iy0 and β = x1 + iy1
These coefficients represent the probability of the qubit being in
the |0> or |1> state.
Upon measurement, a qubit will collapse into either the |0> or |1>
state, but before measurement, there is only the probability that
the qubit is in a particular state.
|α|2 is the probability of |0> |β|2 is the probability of |1>
|α|2 + |β|2 = 1 since the probabilities must sum to one.
Quantum Physics is probabilistic

z
y
θ
φ
|ψ>
Classical 2-state Probabilistic System
If p is the probability of state x, then state y has a probability of
(1-p).
The canonical example is that of flipping a fair coin:
Probability of T = ½, so therefore the probability of H = (1-
½) = ½.
A classical probabilistic system can be thought of as a
probabilistic bit, or pbit.
Ignoring for the moment that it is incorrect use of the ket
notation, a pbit can
be represented the same way as a qubit:
|outcome> = a|0> + b|1> where a = p and b = (1-p)
So in the coin example, the outcome is = ½|T> + ½|H>

z
y
θ
φ
|ψ>
Comparisons
•Bit is 1-D point in only one of two states, 0 and 1.
•Pbit is a 2-D line between the two states 0 and 1
•Qubit is a 3-D sphere with 0 and 1 at the poles, and an infinite
number of superpositions as points on the sphere

z
y
θ
φ
|ψ>
Sphere representations of a qubit
The reason a qubit is represented as a sphere is because the
coefficients are
complex numbers. The probability from 0 to 1 is the similar to
classical
probability, but the complex coefficient introduces an additional
parameter,
phase angle. The spheres below represent three different qubits
with the
same probability proportions of “0-ness” and “1-ness”, but with
different phases.

z
y
θ
φ
|ψ>
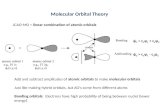
Bloch Sphere
Because |α|2 + |β|2 = 1, the
superposition equation
|ψ> = α|0> + β|1>
may be re-written in polar coordinate
fashion as:
|ψ> = eiγ(cosθ/2 |0> + eiφsinθ/2 |
1>)
Since the factor eiγ has no observable
effects, it can be ignored, so we can
effectively write:
|ψ> = cosθ/2 |0> + eiφsinθ/2 |1>It is important to note that the Bloch sphere is a unit sphere—
that is, every point on the surface of the sphere can be described
by a unit vector—a vector of length 1. It is easy to see then, that
every possible state is a unit vector. Therefore, any state of a
qubit can be described by a vector, and the vectors may be
manipulated mathematically.

z
y
θ
φ
|ψ>
Why does the phase matter?
Phase becomes important when adding together the effects of a
computational operation on all the terms in a superposition. For
example, consider a pair of qubits A and B:
|ψA> = α|0> + β|1> and |ψB> = α|0> - β|
1>
Individually, they both have the same probability |α|2 of |0>, and
since |β|2 = |-β|2, they both have the same probability of |1>.
Now however, consider a specific quantum computation for which
the output is defined to be:
[(α+β)/√2]|0> + [(α-β)/√2]|1>

z
y
θ
φ
|ψ>
Why does the phase matter? (cont.)
Using qubit A, the output is [(α+β)/√2]|0> + [(α-β)/√2]|1>,
but using qubit B, the output is [(α-β)/√2]|0> +
[(α+β)/√2]|1>. The only difference in the output is the sign
of β in the coefficients. As a special illustrative case, set α =
β = 1/√2. In this case, the measured answer of from qubit A
will always be |0>, and the measured answer from qubit B
will always be |1>.
Even though A and B have the same proportions of “0-ness”
and “1-ness”, because the phase is different, they will
produce different measurements.

z
y
θ
φ
|ψ>
Qubit gatesIn order to perform any real computation, we need gates to act
upon the qubits! In classical computation, the familiar gates are
not, and, or, xor, and others which take bits as the input(s), and
combine them in a logical manner to produce an output. Since
the states and operations are entirely different, traditional logic
gates will not work on qubits, but there do exists some analogs.
NOT
Since α|0> + β|1> is a unit vector, it can be represented as a matrix
If a NOT function is applied, the vector becomes α|1> + β|0>, or
The NOT itself may be represented as a matrix
In matrix form then, =

z
y
θ
φ
|ψ>
Matrix manipulations
Can any matrix manipulation be performed on a qubit?➢No, not just any manipulation
The normalization condition requires that |α|2 + |β|2 = 1 for the
state |ψ> = α|0> + β|1>. This must also be true of the resultant
state |ψ'> = α'|0> + β'|1> after the gate has acted.
The condition the gate must adhere to in order to achieve the
constraint is known as the unitary condition. In order for a unit
function matrix U to act, U†U = I, where U† is the conjugate
transpose of U (obtained by transposing and then complex
conjugating U), and I is the 2x2 identity matrix. This is the only
constraint on quantum gates. Any unitary matrix specifies a valid
quantum gate!

z
y
θ
φ
|ψ>
Single qubit quantum gates
•In classical computing, the NOT gate is the only non-trivial single-bit gate.
•In quantum computing, there are many non-trivial single-qubit gates.
•Already shown the NOT (X) gate:
•One important gate is the phase shift (Z) gate:
•One most useful is the Hadamard (H) gate:
•The z rotation (Zϕ) gate rotates the vector around the
z axis, :
•In addition to the z rotation, gates exist for x and y rotations also.

z
y
θ
φ
|ψ>
Multiple qubit quantum gates
•Prototypical multiple-qubit gate is the controlled-NOT, or CNOT gate.
•Two qubit inputs—one the control and the other the target.
•If the control qubit is set to 0, then the target qubit is not changed.
•If the control qubit is set to 1, then the target qubit is flipped.
|00>⇒|00>; |01>⇒|01>; |10>⇒|11>; |11>⇒|10>;
CNOT =

z
y
θ
φ
|ψ>
Multiple qubit quantum gates cont.
Inputs Outputs
a b c a' b' c'
0 0 0 0 0 0
0 0 1 0 0 1
0 1 0 0 1 0
0 1 1 0 1 1
1 0 0 1 0 0
1 0 1 1 0 1
1 1 0 1 1 1
1 1 1 1 1 0
Quantum gates cannot be used directly to simulate classical
logic gates because quantum gates are reversible (they have
an inverse) while classical gates do not. However, the Toffoli
gate can be used to simulate any classical using reversible
quantum gates, even though the Toffoli gate is itself reversible.
Toffoli gate truth table

z
y
θ
φ
|ψ>
● The state of a register of n qubits has 2n different dimensions (rather than 2n dimensions with 2n different values).
● This exponential growth of the state space is what really gives quantum computing its “bang for the buck”.
● A number of these dimensions cannot be represented as simple products of the states of individual qubits; these are referred to as entangled states.
● When the state of two qubits is entangled, an operation that affects one of them (i.e. measuring it) also affects the other qubit
Multiple Qubits and Quantum Entanglement

z
y
θ
φ
|ψ>
● This entanglement leads to some truly hard-to-explain quantum effects, such as the Einstein-Podolsky-Rosen (EPR) Paradox.
– Suppose you take two entangled qubits, and give one to Alice and one to Bob. They move far apart.
– Now Alice measures the state of her qubit – suppose she measures a |0>.
– If Bob now measures his qubit, he will measure the same thing.
– This seems to imply that it is possible to communicate instantaneously across any distance (i.e. faster than the speed of light), violating laws of physics.
Entanglement (cont.)

z
y
θ
φ
|ψ>
● In fact, it turns out that even though this action at a distance seems to happen, it cannot be used to actually communicate – whew, relativity saved again!
● But it can be used for quantum teleportation, dense coding, and key distribution, some important applications of quantum theory that have been experimentally proven.
Entanglement (cont.)

z
y
θ
φ
|ψ>
Quantum Parallelism
● Given some universal function Uf, it is simultaneously
applied to each basis vector in the superposition of its inputs – this generates the superposition of the results.
● This in conjunction with entanglement is the reason for the excitement about quantum computing – there are a huge number of possible superpositions of states, and computations can be done on all of these superpositions in parallel.

z
y
θ
φ
|ψ>
Quantum Circuits
● Quantum circuits or networks are analogous to digital electronic circuits – a set of quantum gates connected together to perform a specific operation.
● In addition to interconnected gates, the circuit can include measurement points.
U1 U2 U3
M

z
y
θ
φ
|ψ>
Quantum Circuits (cont.)● Because a state cannot be copied or cloned, fan-out from a
gate is not allowed.
● Simple example – quantum half-adder.
● There are a number of different possible sets of universal quantum gates.

z
y
θ
φ
|ψ>
Quantum Computers
● Requirements for quantum hardware:
– Scalable, with well-characterized qubits
– Initializable to a pure state such as |00…0>
– Relatively long decoherence time
– Universal set of quantum gates
– Qubit-specific measurement capability
– Ability to faithfully communicate qubits

z
y
θ
φ
|ψ>
Quantum Computers (cont.)
● Possible technologies for creating and connecting qubits:
– Ion traps
– Nuclear Magnetic Resonance (NMR)
– Solid-state (semiconductor quantum dots)
– Optical lattices
● None of these has yet exhibited much scalability.

z
y
θ
φ
|ψ>
Quantum Computers (cont.)
● Ion Traps
– One of the first implemented mechanisms
– Small number of ions trapped using electromagnetic fields
– Ions manipulated using laser pulses
– Progress is being made on producing lattices of ion traps, some of which store ions (memory) and some of which allow interactions (computation units)
– Ion trap hardware used to implement the Deutsch–Jozsa algorithm in 2002

z
y
θ
φ
|ψ>
● NMR
– Another early mechanism – liquid-based two qubit device built in 1998.
– Qubits stored in nuclear spin of hydrogen atoms, constrained by magnetic fields.
– Spins manipulated using radio waves.
– Most advanced computer to date is a seven-qubit device built using NMR techniques – implemented Shor’s algorithm.
Quantum Computers (cont.)

z
y
θ
φ
|ψ>
Quantum Computers (cont.)
● Solid-state devices
– First proposed in 1998.
– Early implementation used the spin of a phosphorus nucleus, qubit controlled and observed via radio waves.
– Qubits placed within a grid of silicon electrodes
– Believed by many to be the best chance for long-term viable hardware implementation.
– Another possibility – Superconducting Quantum Interference Devices (SQUIDs)

z
y
θ
φ
|ψ>
Error Correction
● One big problem with quantum computers is decoherence – interaction of the particles representing qubits with the outside environment causes a deterioration of the state of the qubit.
● Since the qubits can’t be completely isolated from the external world, need a way to correct the deterioration – quantum error correction
● This is difficult, because you cannot copy or clone a quantum state

z
y
θ
φ
|ψ>
Error Correction (cont.)
● Characterization of errors:
– No errors (I)
– Bit flip errors (X)
– Phase errors (Z)
– Bit flip/phase errors (Y)● Qubit error is a transformation formed by a linear
combination of these components e1 I + e2 X + e3 Y + e4 Z

z
y
θ
φ
|ψ>
● Quantum error correction can be done similarly to classical error correction – add parity qubits and define a transform SC (the syndrome extraction operator) such
that for a given set of n data qubits and k parity qubits C(x) which has been transformed by a correctable error, applying SC identifies which error occurred.
That is,i = SC(Ei(C(x)))
Error Correction (cont.)

z
y
θ
φ
|ψ>
● Error correction proceeds as follows:
– Apply SC to quantum state padded with |0> bits:
– This will generate a superposition of errors associated with their respective index.
– Measure the |i> component of the result – yields a value i0
and projects the state to
iiEe
iEeS iiiic 0
0,0 iEi
Error Correction (cont.)

z
y
θ
φ
|ψ>
– Now apply the inverse of the error transform Ei0 to the first n
+ k qubits to get the corrected state
– We only need to do one inverse transform, because the second step projected multiple error transformations onto a single error.
● The errors that can occur (and their frequency) is dependent on the quantum hardware implementation. The correction would need to be built into the software or the hardware.
Error Correction (cont.)

z
y
θ
φ
|ψ>
Future Direction
● One researcher, Marshall Stoneham at University College London, is working on a silicon-based approach, and he predicts that there could be desktop quantum computers by 2010.
– (Is this guy a programmer trapped in a physicist’s body? We all know how good software people are at time estimates …)

z
y
θ
φ
|ψ>
References
http://www.cs.caltech.edu/~westside/quantum-intro.html
Introduction to Quantum Information Processing. A paper by Krill, et. al., from 2002.
An Introduction to Quantum Computing for Non-Physicists. A paper by Rieffel and Polak, found in ACM Computing Surveys, Vol. 32, No. 3, September 2000, pp. 300-335.
Jenny Hogan, “Quantum Bits and Silicon Chips”, Nature, Vol. 24, 31 July 2003, pp. 484-486.
http://videos.dac.com/videos/40th/51/51_1/51_1slides.pdf

z
y
θ
φ
|ψ>z
y
θ
φ
|ψ>
Questions?(... sure, like we'll be able to answer them ... )

z
y
θ
φ
|ψ>
Don’t touch that dial…
Stay tuned next time, when we’ll see how you actually program one of these
things to do something useful.









![Biological Research in India - · PDF fileRamachandran plot or a [φ,ψ] plot developed in 1963 by G. N. Ramachandran, C. ... biotechnology, bioinformatics, and the various ‘omics’](https://static.fdocument.org/doc/165x107/5ab3b6597f8b9a1d168ea056/biological-research-in-india-plot-or-a-plot-developed-in-1963-by-g-n.jpg)