What is Quantization?What is Quantization? · 2020-01-01 · Quantization of Algebraic Curves •...
Transcript of What is Quantization?What is Quantization? · 2020-01-01 · Quantization of Algebraic Curves •...

What is Quantization?What is Quantization?What is Quantization?

“Quantum Symplectic Geometry”
symplectic manifold(Hilbert space)H
algebra of functionson
(algebra of operators)A
Lagrangian submanifoldvector P 2222 H
A = 0^
P = 0i
A i
(M, ω)
M
L 3333 M

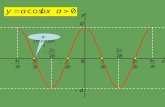
The simplest example
symplectic manifold:
Lagrangian submanifoldvector P 2222 H
A(x,y) = 0 P = 0
parametrized by
A (x,y;q)^ ^^

What is expected …
PA(x,y)=0
A

The First Surprise
A(x,y) polynomial in x,y
and

Quantization of Algebraic Curves
• For any closed cycle:
[S.G., P.Sulkowski]
• Has an elegant interpretation in terms of algebraic K-theory and the Bloch
group of �

Quantization of Algebraic Curves
• For any closed cycle:
Example:
A(x,y) = 1 - (x - x - 2 - x + x )y + y-4 -2 42 2
B(x,y) = 1 - (x - x - 2 - x + x )y + y-6 -2 62 2
Has all the symmetries, but is NOT A-polynomial of any knot

Geometric Representation Theory
e.g. SL(2,�)
e.g. SL(2,�)
e.g. SU(2)
G = real form of G� �
G = complexification of G�
G = (simple) compact Lie group
• Let O (x) = G , x be a coadjoint orbit
through an element x , where� �
an example of a symplectic manifold!

More Surprises
• there exist unitary representations that
don’t appear to correspond to orbits,
e.g. complementary series
• conversely, there are real orbits that don’t seem to correspond to unitary representations.
M = O�
real coadjoint orbit of G�
representation of G�
: [Borel-Weil-Bott][Harish-Chandra]
: [B.Kostant]
[A.A.Kirillov][D.Vogan]
[R.Brylinski][N.Berline, M.Vergne]
:
Puzzles (lessons for quantization):

More Surprises
M = O�
real coadjoint orbit of G�
representation of G�
Puzzles (lessons for quantization):
= minimal orbit of SO(p,q) type B
(p+q = odd)
exists if p #### 3 or q #### 3does not exist if p,q PPPP 4
[D.Vogan, …]

More Surprises
M = O�
real coadjoint orbit of G�
representation of G�
Puzzles (lessons for quantization):
• Both of these issues can be resolved at the cost of replacing classical geometric objects (namely, coadjoint orbits) with their quantum or “stringy” analogs (branes).
[S.G., E.Witten]

Brane Quantization
Puzzle 1: complementary series?
M = O�
real coadjoint orbit of G�
representation of G�
Puzzle 2: = minimal orbit of SO(p,q) type B
There is a corresponding A-brane!
Lagrangian brane supported on M is a good
object in the Fukaya category of Y = M only if
is a mod 2 reduction of
a torsion class in the integral cohomology of M.
�

Quantization: Uniqueness?Quantization: Uniqueness?Quantization: Uniqueness?

Integrable Systems
Spectral curve:
Baxter equation
A(x,y) = 0
Q = 0
in
A (x,y;q)^ ^^

XXZ magnet and sinh-Gordon
Spectral curve:
Baxter equation: Q = 0A (x,y;q)^ ^^

Trigonometric Ruijsenaars-Schneider
Baxter equation: Q = 0A (x,y;q)^ ^^
Spectral curve:
has a simple solution:

Two Different Quantizations
[A.Gadde, S.G., P.Putrov]
P = 0A (x,y;q)^ ^^Q = 0A
^Baxter

Complex Chern-SimonsComplex ChernComplex Chern--SimonsSimons

Quantization of
LLLL = line bundle
overwith

E.Verlinde
Example: G=SU(2) g=2
Quantization of

Complexification
-valued connectionG�
moduli space of Higgs bundleshyper-Kahler
ω
I
ω
J
ω
K
I J K conj.

Complexification
-valued connectionG�
circle action

Equivariant Verlinde Formula
Example: G=SU(2)
[S.G., D.Pei]

New 2d/ 3d TQFT
• “equivariant Higgs vertex”
• 3d-3d correspondence (equivariant integration over Hitchin moduli space)
• Equivariant G/G model on S
• Abelian 2d theory on the Coulomb branch
• Topological twist of 3d N=2 adjoint SQCD (equivariant quantum K-theory of vortex moduli space)

Classifying Phases of MatterClassifying Phases of MatterClassifying Phases of Matter

Quiver Chern-Simons theory
cf. [D.Belov, G.Moore][A.Kapustin, N.Saulina]
[J.Fuchs, C.Schweigert, A.Valentino]:
avertex U(1) Chern-Simons at level a
a
edge
ai
aj

Quiver Chern-Simons theory
integrate out A

3d Kirby moves

3d Kirby moves
A is Lagrange multiplier
Integrating out A makes B pure gaugeand removes all its Chern-Simons couplings

Plumbing graphs
Intersection form on :

Kaluza-Klein compactification
6d fivebrane theory
on � x M6-n
n
“effective” theory T[M ]
in 6-n dimensionsn
depends on topology and
geometry of Mn

4-manifolds VOA’s44--manifolds manifolds VOAVOA’’ss

6 = 2 + 4
4-manifold M42d N = (0,2) theory
T[M ]4
6d fivebrane theory
on � x M2
4depends on topology and
geometry of M4

6 = 2 + 4
4-manifold M42d N = (0,2) theory
T[M ]4
• representations of affine Kac-Moody algebras
• moonshine module / monster symmetry
• affine W-algebras
• chiral de Rham complex
Vertex Operator Algebras:

6 = 2 + 4
4-manifold M4Vertex Operator
Algebra
Heisenberg algebra0-handle
affine Kac-Moodyadding 2-handles: ADE
more general plumbinggraphs, Kirby moves, …
VOAs associated witheven positive lattices …




![G54FOP: Lecture 11psznhn/G54FOP/LectureNotes/lecture11.pdf · G54FOP: Lecture 11 – p.3/21. Capture-Avoiding Substitution (1) [x 7→s]y = s, if x ≡ y y, if x 6≡y [x 7→s](t1](https://static.fdocument.org/doc/165x107/5fb46e9fbf194c18af79d0d2/g54fop-lecture-11-psznhng54foplecturenotes-g54fop-lecture-11-a-p321.jpg)










![-Quantization of Fourier-Mukai transforms · An algebraic result Theorem [Arinkin’06] Suppose • X, Y are smooth qcqs schemes over C; • K ∈ Db coh(X ×Y) is a complex for which](https://static.fdocument.org/doc/165x107/5f5b1345aa54817dac3a2ebc/quantization-of-fourier-mukai-an-algebraic-result-theorem-arinkina06-suppose.jpg)