Submitted bySohanlalRiturajSandeepSanjay KabirSanjay SahuSatyendraShubham GuptaShubham Prajapati

The Trigonometry is derived from a Greek word, trigonon and metron. The word trigonon means a triangle and the word metron means measure. Therefore, trigonometry means the science of measuring triangles.

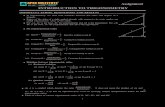
(I) Sin θ = Perpendicular Hypotenuse (ii) Cosine θ = Base Hypotenuse (iii) Tangent θ = Perpendicular Base (iv) Cosecant θ = Hypotenuse Perpendicular (v) Secant θ = Hypotenuse Base (vi) Cotangent θ = Base Perpendicular

Let angle XAY = θ be an acute angle and P be a point on its terminal side AY. Draw perpendicular PM from P on AX .

IN ∆AMP, we have Sin θ = PM, cos θ = AM AP AP and tan θ = PM AM

It is evident from ∆AMP that as θ becomes smaller and smaller, line segment PM also becomes smaller and smaller; finally when θ becomes O ; the point P will ⁰coincide with M. Consequently , we have PM = O and AP=AM Therefore, sin O = PM = O ⁰=O AP AP cos O =AM =AP = ⁰ 1 AP AP

Therefore, sin 90 = PM = PM = 1⁰ AP PM and cos 90 = AM = O = O⁰ AP AP Thus, we have sin 90 = 1 and cos 90 =O⁰ ⁰Remark:- It is evident from

the above discussion that tan 90 = PM =O is not ⁰

defined . Similarly, sec 90 , ⁰cosec 0 , cot o are not ⁰ ⁰defined .

and , tan O = PM = O =O⁰ AP APThus, we have sin O = O, cos O = 1 ⁰ ⁰ and tan O = O⁰From ∆AMP, it is evident that as θ increase, line segment AM becomes smaller and smaller and finally when θ becomes 90 ⁰the point M will coincide with A. Consequently, we have AM =O, AP =PM

Considered an equilateral triangle ABC with each side of

length 2a. Since each angle of an equilateral triangle is of 60 . Therefore, each angle of ⁰∆ABC is of 60 . Let AD be ⁰perpendicular from A on BC. Since the triangle is equilateral the triangle is equilateral. Therefore, AD is the bisector of angle A and D is the mid-point of BC.

Therefore, BD =DC=a and angle BAD =30⁰

Thus, in ∆ABD , angle D is a right angle, hypotenuse AB =2a and BD = a.

So, by Pythagoras theorem, we

Have AB² = AD² + BD² (2a)²= AD² = a² AD²= 4a²- a² AD =√3a Trigonometric Ratios of

30 :⁰In right ∆ ADB, we have

Base =AD = √3a , perpendicular = BD = a, Hypotenuse = AB = 2a and angle DAB= 30 ⁰

sin 30 =BD = a = 1⁰ AB 2a 2 Therefore, cos 30 = AD = √3a = √3⁰ AB 2a 2 tan 30 = BD = a = 1⁰ AD √3a √3 cosec 30 = 1 =2⁰ sin 30⁰ sec 30 = 1 = 2 and cot30 = ⁰ ⁰

√3 cos 30 √3 ⁰

Trigonometry ratios of 60 :⁰ In right triangle ADB, we have Base = BD =a, Perpendicular

=AD= √3a , Hypotenuse =AB = 2a and angle ABD = 60 ⁰

Therefore, Sin 60 = AD =√3a = √3,⁰ AB 2a 2 Cos 60 = BD = a = 1⁰ AB 2a 2 Tan 60 = AD = √3a = √3⁰ BD a Cosec, sec and cot are

opposite of sin, cos, tan respectively.

Consider a right angle triangle ABC with right at B such that angle A= 45 °. Then,

Angle A + Angle B + angle C =180°

45 ° + 90° + Angle C= 180 ° angle C = 45 ° Therefore, angle A = angle C Therefore, AB = BC

Let AB = BC =a. Then , by Pythagoras theorem , we

have AC² = AB² = BC²AC² =a² +a²AC² = 2a²AC =√2aThus, in we have triangle

ABC, we have Angle = 45°, Base = AB =a,

Perpendicular = BC =a, Hypotenuse = AC =√2a

Therefore sin 45= BC = a = 1 AC √2 √2 cos 45° = AB = a = 1 AC √2a √2 tan 45° = BC =a =1 , AB a cosec 45° = 1 = √2 sin 45° sec 45° = 1 = √2 and cos 45° cot 45° = 1 = 1 tan 45°

An equation involving trigonometric ratios of an angle θ (say)is said to be a Trigonometric identity if it is satisfied for all values of θ for which the given trigonometric ratios are defined.

For example, cos² θ – 1cos θ = cos θ ( cos θ – 1) 2 2 is a trigonometric identity, whereas cos θ ( cos θ – 1 ) = 0 2is an equation.