Transfer (Frequency Response) Functions

To characterize the response of a SDOF system to forced vibrations it is useful to define atransfer function or frequency response function between the input and output of thesystem.

HOutput

Input( )Ω = (44)

By normalizing the output of the system with respect to the input, we emphasize thecharacteristics and response of the system over the characteristics of the output or input.

Let's define a transfer function between the steady-state displacement output and forceinput of a SDOF system undergoing forced vibrations:

HDisplacement

Force

u t

Pess

i t( )( )

Ω Ω= = (45a)

H

Pe

k m i cPe

i t

i t( )Ω Ω Ω

Ω

Ω= − +2

(45b)

Hk m i c

( )ΩΩ Ω

=− +

12 (45c)

Hk

in n

( )ΩΩ Ω

=− +

1 1

1 22

2ωβ

ω

(45d)

Notice that the transfer function is a complex-valued quantity meaning the response of theSDOF system can be characterized by a magnitude and phase. Figure 6 shows themagnitude and phase plots for a SDOF system expressed as a function of the normalizedfrequency, nωΩ .

Figure 6 Magnitude and Phase of Transfer Function

Equations 45c and 45d and Figure 6 can be used to provide insight into the parametersthat control the response of a SDOF in different frequency ranges. Note in Equations 45cand d that when Ω→0, the transfer function reduces to:

Hk

( )Ω = =01

(46)

Thus, the stiffness of the system controls the response at low frequency. As Ω→ωn, thetransfer function reduces to:

Hi c ikn( )ΩΩ

= = =ωβ

1 1

2(47)

and the response of the system is controlled to a large extent by the damping in thesystem. Finally, as Ω becomes large, the transfer function becomes:

Hm

( )ΩΩ

→ ∞ ∝−

12 (48)

and the response of the system is largely controlled by the mass (the inertia) of the system.

Other Forms of the Transfer Function

The transfer function defined above was expressed in terms of the displacement. Otherresponse quantities such as the velocity and acceleration of the mass can also be used todefine a transfer function for various applications. The names associated with each ofthese transfer or frequency response functions are given in Table 1.

Table 1 Transfer Functions Used in Vibration Analysis (after Inman, 1994)

Response Parameter Transfer Function Inverse Transfer Function

Displacement Receptance Dynamic Stiffness

Velocity Mobility Impedance

Acceleration Inertance Apparent Mass

Ground Displacement and Acceleration

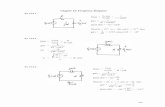
Consider the situation in which the systemvibrates because of motion introduced at thebase of the system, not by a force applied tothe mass. The system is shown at the right.

The forces exerted by the spring and thedashpot on the mass are functions of therelative displacement and velocity betweenthe mass and the base of the system. Theabsolute acceleration of the mass is still used(F=ma).

Thus, the equation of motion of the systembecomes:

mu c u z k u z&& ( & &) ( )+ − + − = 0 (49)

The right hand side is set equal to zero because there are no external forces applied to themass. Rearranging yields:

m

k c

z t( )

u(t)

mu cu ku cz kz&& & &+ + = + (50)

We can assume that the ground motion is given by a harmonic function:

z t Ae i t( ) = Ω (51)

and that the response of the mass is given by:

u t Be i t( ) = Ω (52)

After differentiating, substituting, and solving, we obtain the solution for the steady-statedisplacement of the mass:

u tk i c

k m i cAe i t( ) =

+− +

ΩΩ Ω

Ω2 (53)

We can also define a transfer function between the displacement of the mass and the inputground displacement:

Hu t

z t( )

( )

( )Ω = (54a)

H

k i c

k m i cAe

Ae

i t

i t( )Ω

ΩΩ Ω

Ω

Ω=

+− +2

(54b)

Hk i c

k m i c( )Ω

ΩΩ Ω

=+

− +2 (54c)

H

i

i

n

n n

( )Ω

Ω

Ω Ω=

+

− +

1 2

1 22

2

βω

ωβ

ω

(54d)

As before we can express the complex-valued transfer function in terms of the magnitudeand phase:

Figure 7 Magnitude and Phase of Transfer Function for Ground Displacement

In many earthquake engineering problems,the ground motion input at the base of thesystem is specified in terms of a groundacceleration.

&&( )z t Ce i t= Ω (55)

Furthermore, the response parameter ofinterest is the relative displacement betweenthe base and the mass. The latter is importantbecause it is the relative displacements thatare proportional to the forces induced in thestructure.

y t u t z t( ) ( ) ( )= − (56)

Recall that the equation of motion is:

mu c u z k u z&& ( & &) ( )+ − + − = 0 (49 again)

After substituting Eq. 56 we obtain:

m y z cy ky(&& &&) &+ + + = 0 (55a)

or

my cy ky mz&& & &&+ + = − (57b)

After solving for y(t) we obtain:

y tm

k m i cCe i t( ) =

−− +Ω Ω

Ω2 (58)

Finally, we can define the transfer function between the ground acceleration and therelative displacement of the mass and base:

Hy t

z t( )

( )

&&( )Ω = (59a)

Hm

k m i c( )Ω

Ω Ω=

−− +

(59b)

m

k c

&&( )z t

u(t)

H

i

n

n n

( )ΩΩ Ω

=−

− +

1

1 2

2

2

2

ω

ωβ

ω

(59c)

Figure 8 Magnitude and Phase of Transfer Function for Ground Acceleration