Single-Source Shortest Paths
32
Single-Source Shortest Paths
description
Single-Source Shortest Paths. Contents. Definition Optimal substructure of a shortest path Negative-weight edges Cycles Predecessor subgraph Relaxation The Bellman-Ford algorithm Single-source shortest paths in directed acyclic graphs Dijkstra's algorithm. Definition. Definition - PowerPoint PPT Presentation
Transcript of Single-Source Shortest Paths
Single-Source Shortest Paths
2
Contents
Definition
Optimal substructure of a shortest path
Negative-weight edges
Cycles
Predecessor subgraph
Relaxation
The Bellman-Ford algorithm
Single-source shortest paths in directed acyclic graphs
Dijkstra's algorithm
3
Definition
Definition edge weight path weight shortest-path weight: δ(u,v) shortest path
4
Definition
source, destination single-source single-destination single-source single-destination all pair
5
Optimal substructure of a shortest path
Optimal substructure of a shortest path the shortest path consists of shortest subpath
6
Optimal substructure of a shortest path
Lemma 24.1 Given a weighted, directed graph G = (V, E) with weig
ht function w : E → R, let p = v1,v2,..., vk be a shortest path from vertex v1 to vk and, for any i and j such that 1 ≤ i ≤ j ≤k, let pij = vi, vi+1,..., vj be the subpath of p from vertex vi to vj .
Then, pij is a shortest path from vi to vj.
7
Optimal substructure of a shortest path
Proof If we decompose path p into , v1 vi vj vk then w
e have that w(p) = w(p1i) + w(pij) +w(pjk).
Now, assume that there is a path from vi to vj with weight w(p′ij)< w(pij). Then, v1 vi vj vk is a path from v1 to vk whose weight w(p1i)+w(p′ij)+w(pjk) is less than w(p), which contradicts the assumption that p is a shortest path from v1 to vk.
p1i pij pjk
p1i pij pjk
8
Negative-weight edges
Negative-weight edges Negative-weight edges are permitted if negative-weight
cycles are not reachable from s.
3 -1
5 11
-∞ -∞
0 -∞
-4
6
-3
3
-6
4
8
72
5
3
a b
gdcs
e f
∞ ∞
∞
h i
j
2
3-8
Figure 24.1
9
Cycles
Cycles A shortest path does not include cycles. A shortest path is of length at most |V|-1.
10
Predecessor subgraph
Predecessor subgraph shortest-path tree for example : shows a weighted , directed graph and tw
o shortest-paths trees with the same root.
11
Predecessor subgraph
Figure 24.2 (a)
0s
3t
5y
9x
11z
3
2 12 7
6
4
3
6
5
12
Predecessor subgraph
Figure 24.2 (b)
0s
3t
5y
9x
11z
3
2 12 7
6
4
3
6
5
13
Predecessor subgraph
Figure 24.2 (c)
0s
3t
5y
9x
11z
3
2 12 7
6
4
3
6
5
14
Relaxation
Relaxation definition path-relaxation property
952
752
Relax(u,v,w)
652
652
Relax(u,v,w)
u v
u v u v
u v
15
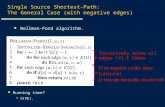
The Bellman-Ford algorithm
The Bellman-Ford algorithm Running time : O(VE) it solves the single source shortest-paths problem in the
general case in which edge weights may be negative.
16
The Bellman-Ford algorithm
5
s
zy
6
7
8-3
72
9
-2xt
-4
order (t,x), (t,y), (t,z), (x,t), (y,x), (y,z), (z,x), (z,s), (s,t), (s,y)
s
zy
6
7
8-3
72
9
-2xt
-4
5
17
The Bellman-Ford algorithm
order (t,x), (t,y), (t,z), (x,t), (y,x), (y,z), (z,x), (z,s), (s,t), (s,y)
s
zy
6
7
8-3
72
9
-2xt
-4
5
s
zy
6
7
8-3
72
9
-2xt
-4
5
18
The Bellman-Ford algorithm
s
zy
6
7
8-3
72
9
-2xt
-4
5
order (t,x), (t,y), (t,z), (x,t), (y,x), (y,z), (z,x), (z,s), (s,t), (s,y)
19
Single-source shortest paths in directed acyclic graphs
Single-source shortest paths in directed acyclic graphs Running time : O(V+E) time starts by topologically sorting the dag to impose a linea
r ordering on the vertices. just one pass over the vertices
20
Single-source shortest paths in directed acyclic graphs
0∞ ∞∞ ∞∞r s t x y z
5
3
2
6
7 -1 -2
1
42
0∞ ∞∞ ∞∞r s t x y z
5
3
2
6
7 -1 -2
1
42
21
Single-source shortest paths in directed acyclic graphs
0∞ 62 ∞∞r s t x y z
5
3
2
6
7 -1 -2
1
42
0∞ 62 46r s t x y z
5
3
2
6
7 -1 -2
1
42
22
Single-source shortest paths in directed acyclic graphs
0∞ 62 45r s t x y z
5
3
2
6
7 -1 -2
1
42
0∞ 62 35r s t x y z
5
3
2
6
7 -1 -2
1
42
23
Single-source shortest paths in directed acyclic graphs
0∞ 62 35r s t x y z
5
3
2
6
7 -1 -2
1
42
24
Dijkstra's algorithm
Dijkstra's algorithm all edge weights are nonnegative. the running time of Dijkstra's algorithm is lower than th
at of the Bellman-Ford algorithm. Running time :
O (V^2) if we use array O(VlgV + ElgV) if we use a heap (VlgV + E) if we use a Fibonacci heap.
25
Dijkstra's algorithm
DIJKSTRA(G, w, s)
1 INITIALIZE-SINGLE-SOURCE(G, s)
2 S ← Ø
3 Q ← V[G]
4 while Q ≠ Ø
5 do u ← EXTRACT-MIN(Q)
6 S ← S {u}
7 for each vertex v Adj[u]
8 do RELAX(u, v, w)
26
Dijkstra’s Algorithm
s t y x z
0 ∞ ∞ ∞ ∞ 0s
∞
t
∞y
∞
x
∞z
Q
S
10
5
2 3
1
94 6
7
2
27
Dijkstra’s Algorithm
s t y x z
0 ∞ ∞ ∞ ∞
10 5 - -
0s
10
t
5y
∞
x
∞z
Q
S
10
5
2 3
1
94 6
7
2
{s}
28
Dijkstra’s Algorithm
s t y x z
0 ∞ ∞ ∞ ∞
10 5 - -
0s
10
t
5y
∞
x
∞z
Q
S
10
5
2 3
1
94 6
7
2
{s, y}
29
Dijkstra’s Algorithm
s t y x z
0 ∞ ∞ ∞ ∞
10 5 - -
8 14 7
0s
8
t
5y
14
x
7z
Q
S
10
5
2 3
1
94 6
7
2
{s, y}
30
Dijkstra’s Algorithm
s t y x z
0 ∞ ∞ ∞ ∞
10 5 - -
8 14 7
8 13
0s
8
t
5y
13
x
7z
Q
S
10
5
2 3
1
94 6
7
2
{s, y, z, t}
31
Dijkstra’s Algorithm
s t y x z
0 ∞ ∞ ∞ ∞
10 5 - -
8 14 7
8 13
9
0s
8
t
5y
9
x
7z
Q
S
10
5
2 3
1
94 6
7
2
{s, y, z, t}
32
Dijkstra’s Algorithm
s t y x z
0 ∞ ∞ ∞ ∞
10 5 - -
8 14 7
8 13
9
0s
8
t
5y
9
x
7z
Q
S
10
5
2 3
1
94 6
7
2
{s, y, z, t, x}
