ROTATIONAL KINEMATICS

1

Ch8. Rotational KinematicsRotational Motion and Angular

Displacement

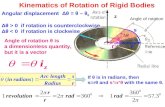
Angular displacement: When a rigid body rotates about a fixed axis, the angular displacements is the angle swept out by a line passing through any point on the body and intersecting the axis of rotation perpendicularly. By convention, the angular displacement is positive if it is counterclockwise and negative if it is clockwise.

SI Unit of Angular Displacement: radian (rad)

2

1. Degree (1 full turn 3600 degree)

2. Revolution (rev) RPM

3. Radian (rad) SI unit

Angular displacement is expressed in one of three units:

3

r

s

Radius

lengtharc

radr

r 22

3.572

3601

rad

(in radians)

For 1 full rotation,

radree 2deg360

4

Example 1. Adjacent Synchronous Satellites

Synchronous satellites are put into an orbit whose radius is r = 4.23*107m. The orbit is in the plane of the equator, and two adjacent satellites have an angular separation of . Find the arc length s.

0.2

5

radiansrees

radiansrees 0349.0)

deg360

2)(deg0.2(0.2

)0349.0)(1023.4( 7 radmrs

)920(1048.1 6 milesm

6

Conceptual example 2. A Total Eclipse of the Sun

7

The diameter of the sun is about 400 times greater than that of the moon. By coincidence, the sun is also about 400 times farther from the earth than is the moon. For an observer on earth, compare the angle subtended by the moon to the angle subtended by the sun, and explain why this result leads to a total solar eclipse.

Since the angle subtended by the moon is nearly equal to the angle subtended by the sun, the moon blocks most of the sun’s light from reaching the observer’s eyes.

8

moon

moonmoon r

s

moonmoon diameters

sun

sunsun r

s sunsun diameters

moonsun ss 400 moonsun rr 400

Since they are very far apart.

9

moon

moonmoon r

diameter

moon

moon

sun

sunsun r

diameter

r

diameter

400

400

moon

moon

moon

moon

r

s

r

diameter

10

moonsun total eclipse

Since the angle subtended by the moon is nearly equal to the angle subtended by the sun, the moon blocks most of the sun’s light from reaching the observer’s eyes.

11

Check Your Understanding 1

Three objects are visible in the night sky. They have the following diameters (in multiples of d and subtend the following angles (in multiples of 0) at the eye of the

observer. Object A has a diameter of 4d and subtends an angle of 20. Object B has a diameter of 3d and subtends

an angle of 0/2. Object C has a diameter of d/2 and

subtends an angle of 0/8. Rank them in descending order

(greatest first) according to their distance from the observer.

12

sr ds

r

00

2

2

4

dd

rA 00

6

2

3

dd

rB

000

4

2

8

8

2dd

d

rC ACB rrr

B, C, A

13

CONCEPTS AT A GLANCE To define angular velocity, we use two concepts previously encountered. The angular velocity is obtained by combining the angular displacement and the time during which the displacement occurs. Angular velocity is defined in a manner analogous to that used for linear velocity. Taking advantage of this analogy between the two types of velocities will help us understand rotational motion.

14

DEFINITION OF AVERAGE ANGULAR VELOCITY

SI Unit of Angular Velocity: radian per second (rad/s)

15

Example 3. Gymnast on a High Bar

A gymnast on a high bar swings through two revolutions in a time of 1.90s. Find the average angular velocity (in rad/s) of the gymnast.

16

revolution

radianssrevolution

1

200.2

radians6.12

17

Instantaneous angular velocity is the angular velocity that exists at any given instant.

The magnitude of the instantaneous angular velocity, without reference to whether it is a positive or negative quantity, is called the instantaneous angular speed. If a rotating object has a constant angular velocity, the instantaneous value and the average value are the same.

t t t

18

In linear motion, a changing velocity means that an acceleration is occurring. Such is also the case in rotational motion; a changing angular velocity means that an angular acceleration is occurring.

CONCEPTS AT A GLANCE The idea of angular acceleration describes how rapidly or slowly the angular velocity changes during a given time interval.

19

DEFINITION OF AVERAGE ANGULAR ACCELERATION

SI Unit of Average Angular Acceleration: radian per second squared (rad/s2)

The instantaneous angular acceleration is the angular acceleration at a given instant.

20

Example 4. A Jet Revving Its Engines

A jet awaiting clearance for takeoff is momentarily stopped on the runway. As seen from the front of one engine, the fan blades are rotating with an angular velocity of –110 rad/s, where the negative sign indicates a clockwise rotation .

As the plane takes off, the angular velocity of the blades reaches –330 rad/s in a time of 14 s. Find the average angular velocity, assuming that the orientation of the rotating object is given by…..

21

The Equations of Rotational Kinematics

22

In example 4, assume that the orientation of the rotating object is given by 0 = 0 rad at time t0 = 0 s. Then, the

angular displacement becomes = – 0 = , and the

time interval becomes t = t – t0 = t.

23

Rotational Motion ( = constant)

Linear Motion (a = constant)

The Equations of Kinematics for Rational and Linear Motion

2

2

1

)(2

1

20

2

20

0

0

tt

t

t

axvv

attvx

tvvx

atvv

2

2

1

)(2

1

20

2

20

0

0

24

Rotational Motion

Quantity LinearMotion

Displacement x

0 Initial velocity v0

Final velocity v

Acceleration a

t Time t

Symbols Used in Rotational and Linear Kinematics

20 2

1tt 22

02

25

Example 5. Blending with a Blender

The blades of an electric blender are whirling with an angular velocity of +375 rad/s while the “puree” button is pushed in. When the “blend” button is pressed, the blades accelerate and reach a greater angular velocity after the blades have rotated through an angular displacement of +44.0 rad (seven revolutions). The angular acceleration has a constant value of +1740 rad/s2. Find the final angular velocity of the blades.

26

0 t

+44.0 rad +1740 rad/s2 ? +375 rad/s

220

)0.44)(/1740(2)/375( 22 radsradsrad

srad /542

27


00 revolution2 radian22

The blades of a ceiling fan start from rest and, after two revolutions, have an angular speed of 0.50 rev/s. The angular acceleration of the blades is constant. What is the angular speed after eight revolutions?

sradsradsrevf //25.0/5.0

What can be found next?

28

220

2 f

22202

2/8

14.3

8srad

after eight revolution, 288 revolution

220

2 f22 )2(28

820

srevsradf /1/2 1.0 rev/s

29

Angular Variables and Tangential Variables

For every individual skater, the vector is drawn tangent to the appropriate circle and, therefore, is called the tangential velocity vT.

The magnitude of the tangential velocity is referred to as the tangential speed.

30

If time is measured relative to t0

= 0 s, the definition of linear acceleration is given by Equation 2.4 as aT = (vT – vT0)/t, where vT

and vT0 are the final and initial

tangential speeds, respectively.

t

rt

rr

t

vva TT

T000 )()(

)/( sradinrvT

)/( 2sradinraT

31

Example 6. A Helicopter Blade

A helicopter blade has an angular speed of = 6.50 rev/s and an angular acceleration of = 1.30 rev/s2. For points 1 and 2 on the blade, find the magnitudes of (a) the tangential speeds and (b) the tangential accelerations.

32

(a)

(b)

33

Centripetal Acceleration and Tangential Acceleration

r

va T

c

2

(centripetal acceleration)

34

The centripetal acceleration can be expressed in terms of the angular speed by using vT = r

While the tangential speed is changing, the motion is called nonuniform circular motion.

Since the direction and the magnitude of the tangential velocity are both changing, the airplane experiences two acceleration components simultaneously.

aT

aC

raT C

T

a

atan

22Tc aaa

35


sradsrev /217/17 smvT /32rv

The blade of a lawn mower is rotating at an angular speed of 17 rev/s. The tangential speed of the outer edge of the blade is 32 m/s. What is the radius of the blade?

0.30 m

21732 r

3.0217

32

r

36

Example 7. A Discus Thrower

Discus throwers often warm up by standing with both feet flat on the ground and throwing the discus with a twisting motion of their bodies. A top view of such a warm-up throw. Starting from rest, the thrower accelerates the discus to a final angular velocity of +15.0 rad/s in a time of 0.270 s before releasing it. During the acceleration, the discus moves on a circular arc of radius 0.810 m.

37

Find (a) the magnitude a of the total acceleration of the discus just before it is released and (b) the angle that the total acceleration makes with the radius at this moment.

(a)

38

(b)

39


00 cast2/0.2 smac

A rotating object starts from rest and has a constant angular acceleration. Three seconds later the centripetal acceleration of a point on the object has a magnitude of 2.0 m/s2. What is the magnitude of the centripetal acceleration of this point six seconds after the motion begins?

0.3t

rvT

40

22 /0.2 smr 22

rr

vac

t 0

3)0.3( t

0.23 2 r

after six second, 660 (=0)

41

at six second

22)0.6( 6 rr t

232 r

234 r

234 r

2/0.80.24 sm8.0 m/s2

42

Rolling Motion

43

)/( sradinrv

)/( 2sradinra

Linear speed

Linear acceleration

Tangential speed, vT

Tangential acceleration, aT

44

Example 8. An Accelerating Car

An automobile starts from rest and for 20.0 s has a constant linear acceleration of 0.800 m/s2 to the right. During this period, the tires do not slip. The radius of the tires is 0.330 m. At the end of the 20.0-s interval, what is the angle through which each wheel has rotated?

45

20 2

1tt

22 )0.20)(/42.2(2

1)0.20)(/0( ssradssrad

rad484

w w0 t

? –2.42 rad/s2 0 rad/s 20.0 s

46

The Vector Nature of Angular Variables Right-Hand Rule Grasp the axis of rotation with your right hand, so that your fingers circle the axis in the same sense as the rotation. Your extended thumb points along the axis in the direction of the angular velocity vector.Angular acceleration arises when the angular velocity changes, and the acceleration vector also points along the axis of rotation. The acceleration vector has the same direction as the change in the angular velocity.

47

Concepts & Calculations Example 9. Riding a Mountain Bike

A rider on a mountain bike is traveling to the left. Each wheel has an angular velocity of +21.7 rad/s, where, as usual, the plus sign indicates that the wheel is rotating in the counterclockwise direction.

48

(a) To pass another cyclist, the rider pumps harder, and the angular velocity of the wheels increases from +21.7 to +28.5 rad/s in a time of 3.50 s.

(b) After passing the cyclist, the rider begins to coast, and the angular velocity of the wheels decreases from +28.5 to +15.3 rad/s in a time of 10.7 s. In both instances, determine the magnitude and direction of the angular acceleration (assumed constant) of the wheels.

(a)

The angular acceleration is positive (counterclockwise).

49

(b)

The angular acceleration is negative (clockwise).

50

Concepts & Calculations Example 10.

A Circular Roadway and the Acceleration of Your Car

51

Suppose you are driving a car in a counterclockwise direction on a circular road whose radius is r = 390 m (see Figure 8.20). You look at the speedometer and it reads a steady 32 m/s (about 72 mi/h). (a) What is the angular speed of the car? (b) Determine the acceleration (magnitude and direction) of the car. (c) To avoid a rear-end collision with a vehicle ahead, you apply the brakes and reduce your angular speed to 4.9 × 10–2 rad/s in a time of 4.0 s. What is the tangential acceleration (magnitude and direction) of the car?

(a)

52

(b)

(c)

53

Problem 5

2)60

min1)(

1

2)(

min74

min/480min/210(

srev

radrevrev

t

REASONING AND SOLUTION Using Equation 8.4 and the appropriate conversion factors, the average angular acceleration of the CD in rad/s2 is

The magnitude of the average angular acceleration is 6.4 × 10-3 rad/s2

23 /104.6 srad

54

Problem 7

REASONING AND SOLUTION Equation 8.4 gives the desired result. Assuming t0 = 0 s, the final angular velocity is

20 0 rad/s (328 rad/s )(1.50 s) 492 rad/st

55

Problem 13

REASONING AND SOLUTION The baton will make four revolutions in a time t given by

t

Half of this time is required for the baton to reach its highest point. The magnitude of the initial vertical velocity of the baton is then

10 2 2

v g t g

56

With this initial velocity the baton can reach a height of

222 20

2 2

9.80 m/s 8 rad6.05 m

2 8 2 radrev8 1.80

s 1 rev

v gh

g

57

Problem 14REASONING AND SOLUTION

r

s

celestial bodyperson on earth

The figure above shows the relevant angles and dimensions for either one of the celestial bodies under consideration.

58

a. Using the figure above

-3

-3

59

b. Since the sun subtends a slightly larger angle than the moon, as measured by a person standing on the earth, the sun cannot be completely blocked by the moon. Therefore, .

a "total" eclipse of the sun is not really total

c. The relevant geometry is shown below.

person on earth

moon

r moon

r sun

s sun

R sun

sun moonsb

Rb

60

The apparent circular area of the sun as measured by a person standing on the earth is given by: , where Rsun is the radius of the sun. The apparent circular area of the sun that is blocked by the moon is , where Rb is shown in the figure above. Also from the figure above, it follows that

2sun sunA R

2blocked bA R

Rsun = (1/2) ssun and Rb = (1/2) sb

Therefore, the fraction of the apparent circular area of the sun that is blocked by the moon is

2 22 2blocked b b b moon sun

2 2sun sun sun sunsun sun

22 3moon

3sun

( / 2)

( / 2)

9.04 10 rad0.951

9.27 10 rad

A R s s r

A s rR s

The moon blocks out 95.1 percent of the apparent circular area of the sun.

61

Problem 17

)75.1)(/0.42(/8.83 20 ssradsradt

REASONING AND SOLUTION Since the angular speed of the fan decreases, the sign of the angular acceleration must be opposite to the sign for the angular velocity. Taking the angular velocity to be positive, the angular acceleration, therefore, must be a negative quantity. Using Equation 8.4 we obtain

srad /3.157

62

Problem 21

REASONING Equation 8.8 from the equations of rotational kinematics can be employed to find the final angular velocity . The initial angular velocity is 0 = 0 rad/s since the top is initially at rest, and the angular acceleration is given as = 12 rad/s2. The angle θ (in radians) through which the pulley rotates is not given, but it can be obtained from Equation 8.1 (θ = s/r ), where the arc length s is the 64-cm length of the string and r is the 2.0-cm radius of the top.

2 20

2

SOLUTION Solving Equation 8.8 for the final angular velocity gives

20

2

63

We choose the positive root, because the angular acceleration is given as positive and the top is at rest initially. Substituting θ = s/r from Equation 8.1 gives

22 20

64 cm2 0 rad/s 2 12 rad/s 28 rad/s

2.0 cm

s

r

64

Problem 29

REASONING AND SOLUTION Equation 8.9 gives the desired result

-3

65

Problem 39

REASONING Since the car is traveling with a constant speed, its tangential acceleration must be zero. The radial or centripetal acceleration of the car can be found from Equation 5.2. Since the tangential acceleration is zero, the total acceleration of the car is equal to its radial acceleration.

SOLUTION

a. Using Equation 5.2, we find that the car’s radial acceleration, and therefore its total acceleration, is

a aR vT

2

r

(75.0 m/s)2

625 m 9.00 m/s 2

66

b The direction of the car’s total acceleration is the same as the direction of its radial acceleration. That is, the direction is

radially inward

67

Problem 42

REASONING The drawing shows a top view of the race car as it travels around the circular turn. Its acceleration a has two perpendicular components: a centripetal acceleration ac that arises because the car is moving on a circular path and a tangential acceleration aT due to the fact that the car has an angular acceleration and its angular velocity is increasing.

68

We can determine the magnitude of the centripetal acceleration from Equation 8.11 as ac = r2, since both r and are given in the statement of the problem. As the drawing shows, we can use trigonometry to determine the magnitude a of the total acceleration, since the angle (35.0) between a and ac is given.

SOLUTION Since the vectors ac and a are one side and the hypotenuse of a right triangle, we have that

0.35cosca

a

69

The magnitude of the centripetal acceleration is given by Equation 8.11 as ac = r2, so the magnitude of the total acceleration is

0.35cosca

a

0.35cos

)/571.0)(5.23(

0.35cos

22 sradmr

2/35.9 sm

70

Problem 46

REASONING AND SOLUTION

a. If the wheel does not slip, a point on the rim rotates about the axle with a speed vT = v = 15.0 m/s

For a point on the rim = vT/r = (15.0 m/s)/(0.330 m)

45.5 rad/s

b. vT = r = (0.175 m)(45.5 rad/s) = 7.96 m/s

=

71

Problem 50

REASONING The angle through which the tire rotates is equal to its average angular velocity multiplied by the elapsed time t, t . According to Equation 8.6, this angle is related to the initial and final angular velocities of the tire by

102t t

The tire is assumed to roll at a constant angular velocity, so that 0 = and = t. Since the tire is rolling, its angular speed is related to its linear speed v by Equation 8.12, v = r, where r is the radius of the tire. The angle of rotation then becomes v

t tr

72

The time t that it takes for the tire to travel a distance x is equal to t = x/v, according to Equation 2.1. Thus, the angle that the tire rotates through is

v v x xt

r r v r

SOLUTION Since 1 rev = 2 rad, the angle (in revolutions) is

3896 000 10 m

= 3.1 10 rad0.31 m

x

r

8 71 rev3.1 10 rad 4.9 10 rev

2 rad

73

Problem 51

74

REASONING Assuming that the belt does not slip on the platter or the shaft pulley, the tangential speed of points on the platter and shaft pulley must be equal; therefore,

rss rp p

SOLUTION Solving the above expression for gives

p ps 2

s

(3.49 rad/s)(0.102 m)28.0 rad/s

1.27 10 m

r

r

s

75

Problem 60

REASONING AND SOLUTION

a. The tangential acceleration of the train is given by Equation 8.10 as

2 3 2 2T = = (2.00 10 m)(1.50 10 rad/s ) = 0.300 m/sa r

The centripetal acceleration of the train is given by Equation 8.11 as

2 2 2 2c = = (2.00 10 m)(0.0500 rad/s) = 0.500 m/sa r

76

The magnitude of the total acceleration is found from the Pythagorean theorem to be

2 2 2T c 0.583 m/sa a a

b. The total acceleration vector makes an angle relative to the radial acceleration of

21 1T

2c

0.300 m/stan tan 31.0

0.500 m/s

a

a

77

Problem 67

REASONING AND SOLUTION By inspection, the distance traveled by the "axle" or the center of the moving quarter is

d 2 (2 r ) 4 r

78

where r is the radius of the quarter. The distance d traveled by the "axle" of the moving quarter must be equal to the circular arc length s along the outer edge of the quarter. This arc length is , where is the angle through which the quarter rotates. Thus,

s r

4 r r

so that . This is equivalent to 4 rad

(4 rad)1 rev

2 rad

2 revolutions

ROTATIONAL KINEMATICS

Documents

Transcript of ROTATIONAL KINEMATICS