1 / 34

Rigid Body DynamicsSimulation and Modeling (CSCI 3010U)

Faisal Qureshihttp://vclab.science.uoit.ca

Computer Science, Faculty of Science

2 / 34

Rigid Bodies

!

"

#

!

"

#

Particle RigidBody

3 / 34

Particle vs. Rigid Body DynamicsI State of a particle

I Position pI Velocity v

I State of a rigid bodyI Position pI Velocity vI Orientation θI Angular velocity ω

4 / 34

Coordinate frames

I [x]e is (1, 2) in coordinate frame described by e1 and e2I What is [x]u, i.e., [x]u expressed in u1 and u2?

5 / 34

Coordinate frames

I x = e1 + 2e2I x = [u0]e + c1[u1]e + c2[u2]eI Note that [x]u = (c1, c2), so we are interested in finding values

of c1 and c2.

6 / 34

Coordinate frames

[u0]e + c1[u1]e + c2[u2]e = [x]ec1[u1]e + c2[u2]e = [x]e − [u0]e[

[u1]e [u2]e] [ c1

c2

]=[

c1c2

]=[

[u1]e [u2]e]−1

([x]e − [u0]e)

Change of basis

[x]u =[

[u1]e [u2]e]−1

([x]e − [u0]e)

7 / 34

Coordinate Frames Exercise - Part 1What is [x]u?

8 / 34

Coordinate Frames Exercise - Part 2What is [x]u?

9 / 34

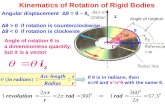
Rigid Bodies in 2D

!"

#

$

Angular VelocityI ω = dθ

dtI Units are radians per secondI Radian is the angle subtended by an arc whose length is equal

to its radious: θ = lr

Linear Velocity at a Point on the BodyI v = rω

10 / 34

Rigid Bodies in 3DI Unlike 2D, orientation in 3D cannot be described using any

angle.I There are many schemes for describing rotations in 3D.I We will use a 3x3 rotation matrix RI We need to find the relationship between angular velocity and

rotation matrix.

We will return to this later.

11 / 34

Equations of Motions for Rigid BodiesForce acting on a Rigid BodyI Net force acting on an object is the rate of change of its linear

momentum.dPdt

= F

I Linear momentum: P = mv, where m is the mass of theobject and v is its linear velocity

Torque acting on a rigid bodyI Net torque acting on an object (about point o) is the rate of

change of its angular momentum.

dLdt

= N

I Angular momentum: L = Iω, where I is the inertia tensor andω is its angular velocity (about point o)

12 / 34

Torque

!Center of mass

"

I Torque (in this example, clockwise or counter-clockwise):

T = d × F

I When force passes through the center of mass, the associatedd vector is zero; therefore, this force produces no torque orrotational effect

13 / 34

Center of Mass (COM)

("#, "%, "&)

World frame

I The center of mass is the mean location of all the mass of thebody.

I The center of mass r is defined as

rx = 1m

∫ρ(x, y, z)xdV

ry = 1m

∫ρ(x, y, z)ydV

rz = 1m

∫ρ(x, y, z)zdV

where ρ(x, y, z) is the density at point (x, y, z).

14 / 34

COM as the origin of the body coordinate frameI Selecting COM as the origin of the body coordinate frame

greatly simpifies the equation of motionsI Any force applied to (or passing through) the COM doesn’t

induce rotation.

Force 1

Force 2

Force 3

Body frame

I Force 1 results in translationonly

I Force 2 results in translationonly

I Force 3 results in bothtranslation and rotation

15 / 34

COM - DiscretizationCenter of mass of a rectangular brick with point masses at its 8vertices

I xi, yi and zi are ith vertexlocation in the worldcoordinates.

I mi is the value of the pointmass at vertex i.

I (rx, ry, rz) is the center ofmass of the rectangular brickin the world coordiantes.

rx =(∑

i

mixi

)/

(∑i

mi

)

ry =(∑

i

miyi

)/

(∑i

mi

)

rz =(∑

i

mizi

)/

(∑i

mi

)

16 / 34

COM - Example% MATLAB Code% 5 ----- 6 % / /|% 4 ----- 3 7% | |/ % 1 ----- 2%

m = ones(1,8) / 8.;

r = zeros(8, 3);r(1,:) = [1, 1, 1];r(2,:) = r(1,:) + [w, 0, 0];r(3,:) = r(2,:) + [0, h, 0];r(4,:) = r(1,:) + [0, h, 0];r(5,:) = r(4,:) + [0, 0, d]; r(6,:) = r(3,:) + [0, 0, d];r(7,:) = r(2,:) + [0, 0, d];r(8,:) = r(1,:) + [0, 0, d];

% compute center of mass firstM = sum(m);

com = ( m(1)*r(1,:) + ...m(2)*r(2,:) + ...m(3)*r(3,:) + ...m(4)*r(4,:) + ...m(5)*r(5,:) + ...m(6)*r(6,:) + ...m(7)*r(7,:) + ...m(8)*r(8,:) ) / M

17 / 34

Inertia TensorI Inertia tensor provides a concise description of the mass

distribution around the center of mass

⎥⎥⎥

⎦

⎤

⎢⎢⎢

⎣

⎡

−−

−−

−−

=

zzyzxz

yzyyxy

xzxyxx

IIIIIIIII

I

∫∫∫∫∫∫

=

=

=

+=

+=

+=

yzdVzyxI

xzdVzyxI

xydVzyxI

dVxyzyxI

dVzxzyxI

dVzyzyxI

yz

xz

xy

zz

yy

xx

),,(

),,(

),,(

))(,,(

))(,,(

))(,,(

22

22

22

ρ

ρ

ρ

ρ

ρ

ρ

18 / 34

Inertia Tensor - Discretization

I =

Ixx −Ixy −Ixz−Iyx Iyy −Iyz−Izx −Izy Izz

I Ixx =

∑imi(y2

i + z2i )

I Iyy =∑imi(z2

i + x2i )

I Izz =∑imi(x2

i + y2i )

I Ixy = Iyz =∑imixiyi

I Ixz = Izx =∑imixizi

I Iyz = Izy =∑imiyizi

I mi are point masses.

19 / 34

Inertia Tensor - Example% CONTINUED FROM PREVIOUS.

% com - center of mass (1x3)% r – vertex locations (8x3)

% now lets compute inertia tensor

rp = r - repmat(com, 8, 1);

I = zeros(3,3);

mrp = repmat(m',1,3) .* rp

I(1,1) = rp(:,2)' * mrp(:,2) + rp(:,3)' * mrp(:,3);I(2,1) = - rp(:,1)' * mrp(:,2);

I(3,1) = - rp(:,1)' * mrp(:,3);

I(1,2) = I(2,1);I(2,2) = rp(:,1)' * mrp(:,1) + rp(:,3)' * mrp(:,3);

I(3,2) = - rp(:,2)' * mrp(:,3);

I(1,3) = I(3,1);

I(2,3) = I(3,2);I(3,3) = rp(:,1)' * mrp(:,1) + rp(:,2)' * mrp(:,2);

20 / 34

Inertia Tensor in the Body Coordinate FrameI The inertia tensor I that we just computed is expressed in the

world coordinate frame. Consequently it changes as theorientation of the rigid body changes.

I We can express the inertia tensor in the body coordinate frame.I We refer to inertia tensor in the body coordinate frame as Ibody.I Ibody doesn’t change as the orientation of the body changes.I Ibody is diagonal, i.e.,

Ibody =

I11 0 00 I22 00 0 I33

I Inverse of Ibody:

I−1body =

1I11

0 00 1

I220

0 0 1I33

21 / 34

Computing IbodyOption 1Diagonalize II Compute eigenvectors and eigenvalues of II Eigenvalues form the diagonal matrix IbodyI Eigenvectors form the 3-by-3 rotation matrix R that describes

the orientation of the rigid bodyI This is the preferred approach

Option 2Use 3-by-3 rotation matrix R that describes the orientationof the rigid bodyI Ibody = RT IR

22 / 34

Inertia TensorI Inertia tensors are available for many canonical objects:

rectangles, circles, spheres, etc.I Efficient algorithms exist to compute inertia tensor, center of

mass, body coordinate frames a given polygonal model of anobject

I Many tools exist to construct polygonal models of 2D/3D rigidobjects

23 / 34

Body coordinate frame

Attach a coordinate framewith each rigid bodyI Origin = center of mass

(defined in the world frame)I Axes = defined in the world

coordinate frame by a 3-by-3rotation matrix R. Columnsof R define the x, y and zaxes of the body coordinateframe

I Inertia tensor Ibody isconstant and diagonal in thisframe

From body coordinate frameto world coordinate frame.

pworld = Rpbody + x

Body frame

! translation

" orientation

#$%&'

#(%)*&

Center of mass

24 / 34

World and Body Coordinate FramesWorld coordinate frameI Collision detection and responseI Display and visualization

Body coordinate frameI Compute quantitites such as inertia tensor once and store them

for later use.

25 / 34

Rigid Body Dynamics

Position ! 1by3vector

Orientation " 3 by3rotationmatrix

LinearMomentum # 1by3vector

AngularMomentum $ 1 by3vector

Mass % scalar

Inertia tensor &'()* 3 by3matrix(inbody frame)

Linear velocity + 1by3 vector

Angular velocity , 1 by3vector

Inertiatensor &-. 3by 3matrix(inworldframe)

Constants

State variables

Derived quantities

Total force / 1by3vector

Totaltorque 0 1 by3vector

26 / 34

Rigid Body DynamicsLinear effectsI dx/dt = vI dP/dt = FI v = P/m

Angular effectsI dR/dt = ω∗R, where 0 −ωx ωy

ωz 0 −ωz−ωy ωx 0

I dL/dt = NI ω = I−1LI I−1 = RI−1

bodyRT

27 / 34

Rigid Body Dynamics

// x - position

state[0] = x[0];state[1] = x[1];

state[2] = x[2];

// R - orientationstate[3] = R[0][0];

state[4] = R[1][0];state[5] = R[2][0];

state[6] = R[0][1];state[7] = R[1][1];

state[8] = R[2][1];state[9] = R[0][2];

state[10] = R[1][2];state[11] = R[2][2];

// P - linear momentum

state[12] = P[0];state[13] = P[1];

state[14] = P[2];

// L - angular momentum

state[15] = L[0];state[16] = L[1];

state[17] = L[2];

// t – OSP needs itstate[18] = 0.0

// dx/dt = v

rate[0] = v[0];rate[1] = v[1];

rate[2] = v[2];

// dR/dt = w* Rdouble[][] Rdot = mult(star(omega), R);rate[3] = Rdot[0][0];

rate[4] = Rdot[1][0];rate[5] = Rdot[2][0];

rate[6] = Rdot[0][1];rate[7] = Rdot[1][1];

rate[8] = Rdot[2][1];rate[9] = Rdot[0][2];

rate[10] = Rdot[1][2];

rate[11] = Rdot[2][2];

// dP/dt = forcerate[12] = force[0];

rate[13] = force[1];rate[14] = force[2];

// dL/dt = torque

rate[15] = torque[0];rate[16] = torque[1];

rate[17] = torque[2];

// dt/dt = 1rate[18] = 1;

odeSolver.step();

// xx[0] = state[0]; x[1] = state[1];x[2] = state[2];

// RR[0][0] = state[3]; R[1][0] = state[4];R[2][0] = state[5];R[0][1] = state[6]; R[1][1] = state[7];R[2][1] = state[8];R[0][2] = state[9]; R[1][2] = state[10];R[2][2] = state[11];R = orthonormalize(R);

// PP[0] = state[12];P[1] = state[13];P[2] = state[14];

// LL[0] = state[15];L[1] = state[16];L[2] = state[17];

Iinv = mult(R, mult(IbodyInv, transpose(R)));omega = mult(Iinv, L);

Init:Flattenstatevariablesintoastatevector

Rate[]encodes 1st orderODEforoursystem

LetODEsolvethestateandthencopythestatebacktoourstatevariables!, #, $

and%.

28 / 34

Rigid Body Dynamics: Numerical ConsiderationsI Over time numerical errors accumulate in rotation matrix RI This effects our computation of I and ωI Orthonormalize R after every timestep

Orthonormalization1. Normalize R1 (excluding last column)2. R1 × R2 = R3 (normalize)3. R3 × R1 = R2 (normalize)

Here Ri represent the i-th row of matrix RErrors were shifted in the matrix

29 / 34

Representing RotationsI We chose to represent rotations as 3-by-3 rotation matricesI Quaternions can be used to represent rotationsI Most rigid body dynamics systems use quaterionsI See Ch. 17 of the textbook

30 / 34

Representing Rigid BodiesI A rigid body has a shape that does not change over timeI It can translate through space and rotateI A rigid body occupies a volume of spaceI The distribution of its mass over this volume determines its

motion or dynamicsI Shape representation is studied extensively in computer

graphics and some areas of mechanical engineering andmathematics

I There are many ways of representing shape, each with adifferent set of advantages and disadvantages

I We will stick to polygons

31 / 34

Shape Representation using PolygonsI The surface of the object is represented by a collection of

polygonsI The polygons are connected across their edges to form a

continuous surfaceI In order to have a well behaved representation we need to

constrain our polygonsI First all of the polygons must be convex, note that we can

always convert a concave polygon into two or more convex ones

Convex Polygon Concave Polygon Non-planar Polygon

Self-intersecting Polygon Triangle

32 / 34

Shape Representation using TrianglesI We will stick to triangles

I Any convex polygon can be converted to a collection oftriangles

AdvantagesI We are only dealing with one type of polygon, a uniform

representationI Triangles are the simplest polygon, makes our algorithms

simplerI Many modeling programs allow us to construct polygonal

modelsI Easy to displayI Many efficient algorithms exist for manipulating triangles

DisadvantagesI Not a compact representationI Not a good approximation for curved surfaces

33 / 34

Other Types of DynamicsI Articulated figures

I Rigid bodies connected by joints and hingesI Used to model the dynamics of human figures

I Vehicle dynamics used to model the dynamics of various kindsof vehicles

I Deformable objectsI Cloth, soft toys, etc.

I These are more complicated than what we have seen so far

34 / 34

ReadingsI Ch. 17 of the textbookI Classical Mechanics (3rd Edition) by H. Goldstein and C.P.

Poole Jr.