On Clustering Financial Time Series - Beyond Correlation
-
Upload
hellebore-capital-limited -
Category
Data & Analytics
-
view
176 -
download
3
Transcript of On Clustering Financial Time Series - Beyond Correlation
ON CLUSTERING FINANCIAL TIME SERIESGAUTIER MARTI, PHILIPPE DONNAT AND FRANK NIELSEN
NOISY CORRELATION MATRICESLet X be the matrix storing the standardized re-turns of N = 560 assets (credit default swaps)over a period of T = 2500 trading days.
Then, the empirical correlation matrix of the re-turns is
C =1
TXX>.
We can compute the empirical density of itseigenvalues
ρ(λ) =1
N
dn(λ)
dλ,
where n(λ) counts the number of eigenvalues ofC less than λ.
From random matrix theory, the Marchenko-Pastur distribution gives the limit distribution asN →∞, T →∞ and T/N fixed. It reads:
ρ(λ) =T/N
2π
√(λmax − λ)(λ− λmin)
λ,
where λmaxmin = 1 + N/T ± 2
√N/T , and λ ∈
[λmin, λmax].
0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0
λ
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
1.6
1.8
ρ(λ
)
Figure 1: Marchenko-Pastur density vs. empirical den-sity of the correlation matrix eigenvalues
Notice that the Marchenko-Pastur density fitswell the empirical density meaning that most ofthe information contained in the empirical corre-lation matrix amounts to noise: only 26 eigenval-ues are greater than λmax.The highest eigenvalue corresponds to the ‘mar-ket’, the 25 others can be associated to ‘industrialsectors’.
CLUSTERING TIME SERIESGiven a correlation matrix of the returns,
0 100 200 300 400 5000
100
200
300
400
500
Figure 2: An empirical and noisy correlation matrix
one can re-order assets using a hierarchical clus-tering algorithm to make the hierarchical correla-tion pattern blatant,
0 100 200 300 400 5000
100
200
300
400
500
Figure 3: The same noisy correlation matrix re-orderedby a hierarchical clustering algorithm
and finally filter the noise according to the corre-lation pattern:
0 100 200 300 400 5000
100
200
300
400
500
Figure 4: The resulting filtered correlation matrix
BEYOND CORRELATIONSklar’s Theorem. For any random vector X = (X1, . . . , XN ) having continuous marginal cumulativedistribution functions Fi, its joint cumulative distribution F is uniquely expressed as
F (X1, . . . , XN ) = C(F1(X1), . . . , FN (XN )),
where C, the multivariate distribution of uniform marginals, is known as the copula of X .
Figure 5: ArcelorMittal and Société générale prices are projected on dependence ⊕ distribution space; notice theirheavy-tailed exponential distribution.
Let θ ∈ [0, 1]. Let (X,Y ) ∈ V2. Let G = (GX , GY ), where GX and GY are respectively X and Y marginalcdf. We define the following distance
d2θ(X,Y ) = θd21(GX(X), GY (Y )) + (1− θ)d20(GX , GY ),
where d21(GX(X), GY (Y )) = 3E[|GX(X)−GY (Y )|2], and d20(GX , GY ) =12
∫R
(√dGX
dλ −√
dGY
dλ
)2
dλ.
CLUSTERING RESULTS & STABILITY
0 5 10 15 20 25 30
Standard Deviation in basis points0
5
10
15
20
25
30
35
Num
ber
of
occ
urr
ence
s
Standard Deviations Histogram
Figure 6: (Top) The returns correlation structure ap-pears more clearly using rank correlation; (Bottom)Clusters of returns distributions can be partly describedby the returns volatility
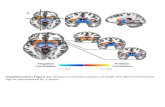
Figure 7: Stability test on Odd/Even trading days sub-sampling: our approach (GNPR) yields more stableclusters with respect to this perturbation than standardapproaches (using Pearson correlation or L2 distances).