Introduction to Algorithms
-
Upload
nicholas-kirkland -
Category
Documents
-
view
58 -
download
1
description
Transcript of Introduction to Algorithms

Introduction to Algorithms
All-Pairs Shortest Paths
My T. Thai @ UF

Single-Source Shortest Paths Problem
Input: A weighted, directed graph G = (V, E) Output: An n × n matrix of shortest-path
distances δ. δ(i, j) is the weight of a shortest path from i to j.
My T. [email protected]
2
1 2 3 4 5
1 0 1 -3 2 -4
2 3 0 -4 1 -1
3 7 4 0 5 3
4 2 -1 -5 0 -2
5 8 5 1 6 0

Can use algorithms for Single-Source Shortest Paths
Run BELLMAN-FORD once from each vertex Time:
If there are no negative-weight edges, could run Dijkstra’s algorithm once from each vertex Time:
My T. [email protected]
3

Outline
Shortest paths and matrix multiplication
Floyd-Warshall algorithm
Johnson’s algorithm
My T. [email protected]
4

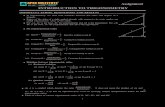
Recursive solution
Optimal substructure: subpaths of shortest paths are shortest paths
Recursive solution: Let = weight of shortest path from i to j that contains ≤ m edges.
Where wij:My T. Thai

Computing the shortest-path weights bottom up
All simple shortest paths contain ≤ n − 1 edges
Compute from bottom up: L(1), L(2), . . . , L(n-1). Compute L(i+1) from
L(i) by extending one
more edge
Time:
My T. [email protected]
6

Shortest paths and matrix multiplication
Extending shortest paths by one more edge likes matrix product: L(i+1)= L(i).W
Compute L(1), L(2), L(4) . . . , L(r) with
My T. [email protected]
8
Time:

Floyd-Warshall algorithm
For path p = <v1, v2, . . . , vl> , v2 … vl-1 are intermediate vertices from v1 to vl
Define = shortest-path weight of any path from i to j with all intermediate vertices in {1, 2, . . . , k}
Consider a shortest path with all intermediate vertices in {1, 2, . . . , k}: If k is not an intermediate vertex, all intermediate vertices
in {1, 2, . . . , k -1} If k is an intermediate vertex:
10

Floyd-Warshall algorithm
Recursive formula:
Time:
My T. [email protected]
11
Note: since we have at most n vertices, return

Constructing a shortest path
is the predecessor of vertex j on a shortest path from vertex i with all intermediate vertices in the set {1, 2, . . . , k}
My T. [email protected]
12
(Use vertex k)

Johnson’s algorithm
Reweighting edges to get non-negative weight edges: For all u, v V∈ , p is a shortest path using
w if and only if p is a shortest path using
For all (u, v) E, ∈ Run Dijkstra’s algorithm once from each vertex
My T. [email protected]
16

Producing nonnegative weights
Construct
Since no edges enter s, has the same set of cycles as G has a negative-weight cycle if and only if G does
Define: Claim:
Proof: Triangle inequality of shortest pathsMy T. Thai
19

Summary
Dynamic-programming algorithm based on matrix multiplication
Define sub-optimal solutions based on the length of paths
Use the technique of “repeated squaring” Time:
Floyd-Warshall algorithm Define sub-optimal solutions based on the set of allowed
intermediate vertices Time:
My T. [email protected]
23

Johnson’s algorithm Reweight edges to non-negative weight edges Run Dijkstra’s algorithm once from each vertex Time: Faster than Floyd-Warshall algorithm when the graph
is dense E = o(V2)
My T. [email protected]
24