Dark Matter and Dark Energy from the solution of the strong CP problem Roberto Mainini, L. Colombo &...
-
Upload
jeffry-blake -
Category
Documents
-
view
217 -
download
3
Transcript of Dark Matter and Dark Energy from the solution of the strong CP problem Roberto Mainini, L. Colombo &...

Dark Matter and Dark Energy from the solution of the strong
CP problem
Roberto Mainini, L. Colombo & S.A. BonomettoUniversita’ di Milano Bicocca
Mainini & Bonometto Phys.Rev.Lett. 93 (2004) 121301Mainini, Colombo & Bonometto (2004) Apj submitted

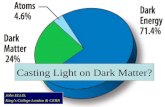
Most cosmological data (CMB, SNIa, LSS) fitted by‘concordance model’ (CDM)
H 70 km/s/Mpc , n 1
ΩDM 0.3 , ΩDE 0.7 , Ωbar 0.04
DE from cosmological constant but….
…. || < 10 -56 cm -2 why so small? (fine-tuning problem)
…. why ΩDM ΩDE ? (coincidence problem)

Dynamical DE models to ease CDM problems
Tracking quintessence
DE from a scalar field self-interacting through an effective potential V() but…. …. at least 1 more parameter required
more complex models to try to unify DM and DE….
Interacting DM-DE models coupling parameter also required

Dual-Axion Model
Axion: DM candidate from Peccei-Quinn (PQ) solution to the strong CP problem
modifying PQ model :
- strong CP problem solved (even better so…)
- DM and DE from single complex scalar field (exploit better the same fields as in PQ approach)
- no fine-tuning
- number of parameter as SCDM (even 1 less than LCDM…) DM an DE in fair proportion from one parameter
- DM and DE coupled (this can be tested) but ….. …..no extra parameter (coupling strength set by theory)
ie2

Strong CP problem
Non-perturbative effects related to the vacuum structure of QCD leads a CP-violating term in LQCD :
Neutron electric dipole moment
Experimental limits on electric dipole moment
GGs ~
2
L
1010
Why θ is so small?

Peccei-Quinn solution and the axion Peccei & Quinn 1977
PQ idea: CP-violating term is suppressed making a dynamical variable driven to zero by the action of its potential
- Additional global U(1)PQ symmetry in SM
- U(1)PQ is spontaneously broken at the scale FPQ
- -parameter is now the NG boson due to sym.br. : the axion Weinberg 1978; Wilczek 1978
with NG potential ie
2 222 )|(||)(| PQFV
PQF

- CP-violating terms generate a potential for the axion which acquires a mass m(T) (chiral symmetry break). From instantonic calculus:
- FPQ is a free parameter
- Cosmological and astrophysical constraints require:
22222
2
1)cos1()( PQPQ FmFmV
)
0)1
PQQCD
QCD
FΛm(T
Λm(T
GeVFGeV PQ1210 1010 eVTmeV 36 102.6)0(102.6

Axion cosmology
- Equation of motion (θ <<1):
- Coherent oscillations for
- Oscillations are damped by the expansion of the universe
- Axions as Dark Matter candidate
Averaging over cosmological time <Ekin> = <Epot>
HTm 2)(
0)(2 22 Tmaa
a
0 potkin EEp )(3 3 Tmaa
a
m
m
30 amT QCD Kolb & Turner 1990

Can a single scalar field account for both DM and DE?
NG potential Tracker quintessence potential with a complex scalar field
no longer constant but evolves over cosmological times
|)(|V
||
PQ model Dual-Axion Model
1)( QCDΛTm
cost
Angular oscillations are still axions while radial motion yields DE
PQF1)( PQQCD FTm
Φ variation cause a dependence of the axion mass on scale factor a

LAGRANGIAN THEORY
AXION DARK ENERGY
)cos1(),()(
2
1 222
TmVgL
0sin)(2 22
Tma
a
a 22 )(2 Va
a
a
)()(3 Cpa
a
022 ma 2)( aC
13 a
)( 3 Ca
a
Friction term modified: moredamping than PQ case
COUPLED QUINTESSENCE MODEL with a time dependent coupling C()=1/
Amendola 2000, 2003

Background evolution
We use SUGRA potential
Note: in a model with dynamical DE (coupled or uncoupled) once ΩDM is assigned can be arbitrarily fixed.
Here is univocally determined
244
)(
GeV
GeVDM10103.0

Background evolution
coupling term settles on different tracker solution
Va 22
22 )(2 Vaa
a

Background evolution
After equivalence the kinetic energy of DE
is non-negligible during matter era

*4
4
DM DM DM DM b b
b b DM DM b b
aC G G
a
aG
a
* 241
3G G
Density fluctuations: linear evolution
modified friction term
DM and baryons fluctuations described by 2 coupled Jeans’ equations:
modified dynamical term

Density fluctuations: linear evolution
Red: dual axion C()=1/Blue: Coupled DE C=cost=<C()>Black: CDM
Differences from CDM:- objects should form earlier - baryons fluct. keep below DM fluct. until very recently

Uncoupled SUGRASUGRA with C = costSUGRA with C= 1/SUGRA Dual-Axion
Fit to WMAP data
- Main differences at low l- 2
eff from 1.064 (uncoupled SUGRA) to 1.071 (C=1/)- SUGRA with C=1/ h=0.930.05
Uncoupled SUGRA
x <x> x
Ωbh2 0.025 0.001
Ωdmh2 0.12 0.02
h 0.63 0.06
0.21 0.07
ns 1.04 0.04
A 0.97 0.13
Log 3.0 7.7
SUGRA with C=cost
x <x> x
Ωbh2 0.024 0.001
Ωdmh2 0.11 0.02
h 0.74 0.11
0.18 0.07
ns 1.03 0.04
A 0.92 0.14
Log -0.5 7.6
0.10 0.07
SUGRA with C= 1/
x <x> x
Ωbh2 0.025 0.001
Ωdmh2 0.11 0.02
h 0.93 0.05
0.26 0.04
ns 1.23 0.04
A 1.17 0.10
Log 4.8 2.4
Best fit parameters:

- One complex scalar field yields both DM & DE
- Fair DM-DE proportions from one parameter : /GeV~1010
- Strong CP problem solved
- DM-DE coupling fixed (C=1/)
- Fluctuation growth is fair
- Structure formation earlier than in CDM
- Fair fit to WMAP data, constraining in the expected range
- SUGRA potential large H0 (~90 10 km/s/Mpc)
- Halo concentration and distribution to be tested, smaller concentrations expected
Conclusions

Dynamical DE models to ease CDM problems
Tracking quintessence
DE from a scalar field self-interacting through an effective potential V() but…. …. at least 1 more parameter required
Ex. : RP model
4
V we have to set the energetic scale
more complex models to try to unify DM and DE….
Interacting DM-DE models
coupling parameter also required

1. Dark Matter (DM): non-baryonic component to account for
dynamics in galaxies and galaxy clusters
1. Dark Energy (DE): smooth component with p<0 to account for cosmic acceleration
Most cosmological data (CMB, SNIa, LSS) fitted by‘concordance model’ (CDM)
Two dark components required:
H 70 km/s/Mpc , n 1
ΩDM 0.3 , ΩDE 0.7 , Ωbar 0.04
DE from cosmological constant but….
…. || < 10 -56 cm -2 why so small? (fine-tuning problem)…. why ΩDM ΩDE ? (coincidence problem)

Axion mass
Φ variation cause a dependence of the axion mass on scale factor aRebounce at z=10 could be critical for structure formation
Maccio’ et al 2004, Phys. Rev. D69, 123516

Some features of coupled quintessence model
• DM particles don’t follow geodesics:
00 xm
mxp
violation of equivalence principle
• Newtonian interactions:
- DM-DM particles - DM- baryons or baryons-barions
2*
3
41GG = effective gravitational constant
ordinary gravitational constant
Modified DM dynamics could be critical for structure formation