Context Free Grammars - E-STUDytoccomp.weebly.com/uploads/3/8/9/3/38938075/3.context_free_gra… ·...
Transcript of Context Free Grammars - E-STUDytoccomp.weebly.com/uploads/3/8/9/3/38938075/3.context_free_gra… ·...

Context Free Grammars
UNIT –III
By
Prof.T.H.Gurav
Smt.Kashibai Navale COE, Pune

Context-Free Grammar
Definition. A context-free grammar is a 4-tuple :
G = (V, T, P, S) OR G = (V, Σ, P, S)
V = Non-terminal(variables) a finite set
T = alphabet or terminals a finite set
P = productions a finite set
S = start variable SV
Productions’ form,
A α
where AV, α (VS T)*: NT NT OR NT T

String generation by CFG
• Generate strings by repeated replacement of non-
terminals with string of terminals and non-
terminals.
1. write down start variable (non-terminal)
2. replace a non-terminal with the right-hand-
side of a rule that has that non-terminal as its
left-hand-side.
3. repeat above until no more non-terminals

Context-Free Languages
• Definition. Given a context-free grammar
• G = (T, NT, P, S), the language generated or derived
from G is the set:
L(G) = {w ε T* | }
• All intermediate stages of the strings resulting from the
start S in the derivation process are called as sentential
form.
• Definition. A language L is context-free if there is a
context-free grammar G = (T, NT, P, S), such that L is
generated from G
S * w

Types of derivations
• There are two ways to derive the string from the grammar
1. Leftmost derivation : When at each step of derivation a production is applied to the leftmost NT, then the derivation is said to be leftmost.
2. Rightmost derivation: When at each step of derivation a production is applied to the rightmost NT, then the derivation is said to be rightmost.

• Consider the following grammar
• S A | A B
• A e | a | A b | A A
• B b | b c | B c | b B
Sample derivations:
S AB AAB aAB aaB aabB aabb
S AB AbB Abb AAbb Aabb aabb
These two derivations use same productions, but in different orders.

Parse Trees
• The pictorial representation of the derivations in
the form of a tree is very useful. This tree is called
parse tree OR derivation Tree.
Root label = start node.
Each interior label = variable.
Each parent/child relation = derivation step.
Each leaf label = terminal or e.
All leaf labels together = derived string = yield.
S
A B
A A B b
a a b

Yield of a parse Tree
• If we look at the leaves of any parse tree and
concatenate them from left to right we get a string
called yield of parse tree.

Derivation Trees/parse trees
Infinitely many others
possible.
S
A B
A A b
a
a
b A
S
A
A A
A A b A
a e
a
b A
S
A B
A A B b
a a b
S A | A B
A e | a | A b | A A
B b | b c | B c | b B
w = aabb Other derivation trees
for this string?
? ?

CFGs & CFLs: Example 1
{an bn | n0}
It is non regular already proved by pumping lemma.
Can be represented by CFG
G = ({S}, {a,b}, {S Є, S a S b}, S)

Example2
Eg: Construct a CFG for language L which has all strings
which are palindromes over ∑={a,b}
Example : madam is palindrome
Gpal=({S}, {a,b}, A, S),
where A={S→e,
S→0,
S→1,
S→0S0,
S→1S1}
Sometimes we group productions with the same head, e.g.
S→e | 0 | 1 | 0S0 | 1S1.

Example
• The string abaaba can be derived as
S start symbol
aSa Rule SaSa
abSba Rule SbSb
abaSaba Rule SaSa
abaЄaba Rule S Є
abaaba is a palindrome

Ambiguty:Defination
• A CFG is ambiguous if there is a string in
the language that is the yield of two or more
parse trees.
• A CFG is ambiguous if there is a terminal
string that has multiple leftmost derivations
from the start variable. Equivalently:
multiple rightmost derivations

Example
Let G={{E},{a,b,-,/},P,E}
P = { EE-E | E/E | a | b} E is start symbol
Solution : Consider the derivation of the string-> a – b/a
Derivation 1 Derivation 2
E=>E-E E=>E/E
E=>a-E/E E=>E-E/E
E=>a-a/E E=> a-E/E
E=>a-a/b E=>a-a/E
E=>a-a/b

Parse trees
E
E E
E E
/
-
a b
a
E
E E
E E
-
/
a b
a

Reasons
• The relative precedence of subtraction and
division are not uniquely defined.
• And two groupings correspond to
expressions with different values.
• It doesn’t captures Associativity!!

Unambiguous G
• Try for a-b/a Now!!
E → E - T | T
T → T / F | F
F → (E) | I
I → a|b

CFG Simplification
Grammar may consists of extra symbols which unnecessarily
increases length of grammar. So simplification needed.
1. Eliminate ambiguity.
2. Eliminate “useless” variables.
3. Eliminate e-productions: Ae.
4. Eliminate unit productions: AB.
5. Eliminate redundant productions.

Eliminate “useless” variables.
• A variable is useful if it occurs in a derivation that begins
with the start symbol and generates a terminal string.
• Two types of the symbols are useless
• A symbol (NT or T )
– Non generating symbols : symbols not generating any terminal
string
– Non reachable symbols : can not be reached from Start symbol.
We use Dependency Graph method to decide not reachable NT.
S aA
BA S aA BA
Here A is Reachable and B is not Reachable from S
A B S

Eliminate e-productions: Ae.
• A CFG may have productions of the form A e . This
production is used to erase A . Such production is called as
null production .
• While eliminating e rule from grammar .. Meaning of
CFG should not be changed.
Example:G= S0S| 1S | e construct G’ generating L(G)-{e}
Solution : Then replace Se in other rules to generate new
rules.
ie S0 and S1
There fore G’ = S0S| 1S| 1 | 0

Eliminate unit productions:
AB
• Unit productions are the productions in which one NT
gives another NT
Eg: AB OR XY
Steps : 1. Select unit production AB , such that there exists
production BX1X2X3…Xn
2. Then while removing AB we should
add A X1X2X3…Xn in the grammar .
eliminate AB from grammar
}

Example
G { S0A | 1B | C
A0S | 00
B1 | A
C01 }
Solution : unit productions are SC BA
We have C01 … So S0A | 1B | 01
We have A0S | 00 … So B0S | 00 | 1
Thus G’ = {S0A | 1B | 01
A0S | 00
B0S | 00 | 1
C01 }

Two normal forms :
1. Chomsky N F
2. Greibach N F

Chomsky Normal Form
• If all rules of the grammar are of the form.
NT NT . NT
NT T
In CNF we have restriction on the length of RHS
and nature of Symbols in RHS of Rules.

Greibach Normal Form
• A CFG is in Griebach Normal Form if each rule is of the form
NT one terminal . Any number of NT
Example
SaA is in GNF
Sa
But SAA Or SAa is not in GNF

Rules: 1. Substitution Rule
Let G=(V,T,P,S) be a given Grammar and if production
A Ba &
B β1 | β2 | β3 | ….| βn
then we can convert A rule to GNF as
A β1a | β2a | β3a | ….| βna
Example : let S Aa and A aA | bA | aAS | b
We can apply rule 1 as
S aAa | bAa | aASa | ba
A aA | bA | aAS

2. Left Recursion Rule
Let G=(V,T,P,S) be a given Grammar and if production
such that βi do not start with A then equivalent grammar in
GNF is :
A β1 | β2 | β3 | ….| βn
A β1 Z | β2 Z | β3Z | ….| βnZ
Z a1 | a2 | a3 | ….| an
Z a1Z | a2Z | a3Z | ….| anZ
A Aa1 | Aa2| Aa3|……| β1 | β2 | β3 | ….| βn

Left linear grammar and right
linear grammar 1. If NT appears as a rightmost symbol in each production
of CFG then it is called right-linear grammar.
2. If NT appears as a leftmost symbol in each production of
regular grammar then it is called left-linear grammar.
• Linear grammars (either left or right) actually produce
the Regular Languages, and also called as regular
Grammar. ( which means that all the Regular Languages are also CF.)

Regular grammars
Right Linear Grammars:
Rules of the forms
A → ε
A → a
A → aB
A,B: variables(NT) and
a: terminal
Left Linear Grammars:
Rules of the forms
A → ε
A → a
A → Ba
A,B: variables(NT) &
A: terminal

RLG to FA
Grammar G is right-linear
Example:
aBbB
BaaA
BaAS
|
|

Steps
Consider grammar G is given , corresponding FA ,
M will be obtained as follows:
1. Initial state of FA will be start NT of G.
2. A Production in G corresponds to transition in M
3. The transitions in M are defined as :
1. Each production AaB gives transition from State A
to B on input alphabet ‘a’.
2. Each production Aa gives transition from State A to
Qf(final state of FA) on input alphabet ‘a’.

Example
Construct NFA , M such that
bBaB
BaA
BaAS
|
|

1. Every state is a grammar variable:
2. Add edges to each production
(a) SaA
SB
(b) AaB
(C) Ba
BbB
S FV
A
B
special final state
a
e
aa
b
L(G) = L(M)

FA to RLG
• Steps :
1. Start State of the FA will become the Start Symbol of the G
2. Create set of Productions as
a. If q0(initial state of the FA) Ԑ F then add a production S Ԑ to P
b. For every Transition of the form ,
add production BaC
a
c.
Add production BaC and Ba
B C
B C a

FA to RLG(example)
Convert FA to a RLG
a
b
a
be
0q 1q 2q
3q

0q 1qa
10 aqq
b
11 bqq
a2q
21 aqq
b
3q
32 | bqbq
e
13 qq
LMLGL )()(

Conversion from RLG to LLG and
Vice versa
fig : From RLG to LLG
Steps :
1 Represent RLG using Transition graph(FA) .
2. Interchange the start state and the Final State .
3.Reverse the directions of all transitions keeping the labels
and the states unchanged.
4. Write left linear G from the changed transition graph.
Right Linear G
Transition Graph
Left Linear G

Properties of CFL
1. The union and concatenation of two context-free languages is context-free, but the intersection need not be.
2. The reverse of a context-free language is context-free, but the complement need not be.
3. Every regular language is context-free because it can be described by a regular grammar.
4. The intersection of a context-free language and a regular language is always context-free.
5. There exist context-sensitive languages which are not context-free.
6. To prove that a given language is not context-free, one may employ the pumping lemma for context-free languages

Pumping lemma for CFL
• Let G be a CFG. Then there exists a
constant ‘n’ such that any string w ε L(G)
with |w|>=n can be rewritten as w=uvxyz,
subject to the following conditions: 1. |vxy|<=n , the middle portion is less than n.
2. |vy| = Є strings v and y will be pumped.
3. For all i>=0 uvixyiz is in L. the two strings v and y can
be pumped zero or more times.

x u z y v

Example 1
• L = {anbncn | n 0}
• Assume L is a CFL,
• Choose w = a2b2c2 in L
• Applying PL, w = uvxyz, where |vy|>0 and |vxy|p, such that uvixyiz in L for all i0
• Two possible cases:
– vxy = (combination of a & b) , uv2xy2z will result in more a’s and/or more b’s than c’s, not in L
– vxy = (combination of b & c), uv2xy2z will result in more b’s and/or more c’s than a’s, not in L
• Contradiction, L is not a CFL

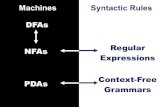
Grammar types
• There are 4 types of grammars according to the types of
rules:
• Each type recognizes a set of languages.
– General grammars → RE languages
– Context Sensitive grammars → CS languages
– Context Free grammars → CF languages
– Linear grammars → Regular languages

Chomsky Hierarchy
• Comprises four types of languages and their associated
grammars and machines.
• Type 3: Regular Languages
• Type 2: Context-Free Languages
• Type 1: Context-Sensitive Languages
• Type 0: Recursively Enumerable Languages
• These languages form a strict hierarchy

1. Type 3 : A є
Aa | aB
ABa
2. Type 2:
Aα
where A ε V and α ε (V union T)*
3. Type 1:
αAβ αXβ with | β | >=| α |
where β ,and X are strings of NT and/or T
with X not NULL and A is NT.

Language Grammar Machine Example
Regular
Language
Regular Grammar
Right-linear
grammar
Left-linear
grammar
Deterministic or
Nondeterministic
Finite-state
Acceptor(FA)
a*
Context-free
Language
Context-free
grammar
Pushdown
automaton(PDA)
anbn
Context-
sensitive
Context-sensitive
grammar
Linear-bounded
Automaton
anbncn
Recursively
enumerable
Unrestricted
grammar
Turing
machine(TM)
Any computable
function

Graph grammars
• Graph grammars has been invented in order
to generalize (Chomsky) string grammars.

Graph grammars: definition
• A graph grammar is a pair:
GG = (G0,P)
G0 is called the starting graph and P is a set of production rules
L(GG) is the set of graphs that can be derived starting with G0 and applying the rules in P

Continue..
• A set of production rules are used to replace
one subgraph by another.
• The process of replacing depends upon the
embedding: edges to/from the old subgraph
must be transformed into edges to/from the
new subgraph.

Types of GG
• Often, on a high level, two kinds of graph grammars are distinguished:
– Hyperedge replacement grammars
• Rewrite rule replaces (hyper)edge by new graph
– Node replacement grammars • Rewrite rule replaces node by new graph

Node replacement grammars
• node replacement grammars with rules of
the form:
N G / E
Node label Labeled graph Embedding rules
Replace any node with label N by G, connecting
G to N’s neighborhood according to the embedding rules listed in E.
Embedding rules are based on node labels.

Example NR-GG rule
N a
c c
/ {(a,b), (b,c)} b b
N
c c
b b
a
a b
c a
N
c c
b b
a
a b
c a

b b a
c c
Example NR-GG rule
N a
c c
/ {(a,b), (b,c)} b b
N
c c
b b
a
a b
c a
c c
b b
a
a b
c a

Production Rules
• Following two types are used to describe
the production rules in GG.
1. Algebraic (using gluing construction)
2. Set theoretic( uses expressions to describe
the embedding

Applications
• Picture processing : A picture can be
represented as a graph , where labelled
nodes represents primitives and labelled
edges represents geometric representations(
such as is right of , is bellow)
• Diagram recognition:

Recursively Enumerable Languages
• A TM accepts a string w if the TM halts in a final state. A
TM rejects a string w if the TM halts in a non final state or
the TM never halts.
• A language L is recursively enumerable if some TM
accepts it. Hence they are also called as Turing
Acceptable L .
• Recursively Enumerable Languages are also called
Recognizable

Input string
Turing Machine for Lacceptq
rejectq
For a Turing-Acceptable language : L
It is possible that for some input string the machine enters an infinite loop

Recursive Language
• Recursive Language : A language L is recursive if some TM
accepts it and halts on every input.
• Recursive languages are also called Decidable Languages
because a Turing Machine can decide membership in those
languages (it can either accept or reject a string).

Input string
Accept
Reject
Decider for L
Decision On Halt:
acceptq
rejectq
For a decidable language : L
For each input string, the computation halts in the accept or reject state

Undecidable Languages
• undecidable language = not decidable language
• If there is no Turing Machine which accepts the
language and makes a decision (halts) for every
input string.
• Note : (machine may make decision for some
input strings)
• For an undecidable language, the corresponding
problem is undecidable (unsolvable):

Applications of RE and CFG in
compilers

Programming
Language
(Source) Compiler
Machine
Language
(Target)
c

The Structure of a Compiler
c

1. RE and FA : Are usually used to classify the basic
symbols (e.g. identifiers, constants,keywords) of a
language.
2. Context free Grammar:
1. Describes the structure of a program.
2. are used to count: brackets: (), begin...end,
if...then...else
c

Lexical Analysis/ Scanning
Converts a stream of characters (input program) into a
stream of tokens.
Terminology
Token: Name given to a family of words.
e.g., integer constant
Lexeme: Actual sequence of characters representing a
word. e.g., 32894
Pattern: Notation used to identify the set of lexemes
represented by a token. e.g., [0 − 9]+
c

Some more examples
Token Sample
Lexemes
Pattern
while while while
integer constant 32894, -1093, 0 [0-9]+
identifier buffer size [a-zA-Z]+
c

Patterns
How do we compactly represent the set of all lexemes
corresponding to a token?
For instance: The token integer constant represents
the set of all integers: that is, all sequences of digits (0–9),
preceded by an optional sign (+ or −).
Obviously, we cannot simply enumerate all lexemes.
Use Regular Expressions.
c

Regular Definitions
Assign “names” to regular expressions.
For example,
digit → 0 | 1 | ··· | 9
natural → digit digit∗
Shorthands:
a+: Set of strings with one or more occurrences of a. a*: Set
of strings with zero or one occurrences of a.
Example:
integer → (+|−)*digit+
c

Regular Definitions and Lexical Analysis
Regular Expressions and Definitions specify sets of strings
over an input alphabet.
They can hence be used to specify the set of lexemes
associated with a token.
That is, regular expressions and definitions can be used as
the pattern language
c

Parsing/ syntax analysis
Main function of parser: Produce a parse tree from
the stream of tokens received from the lexical analyzer
which is then used by Code Generator to produce target
code.
This tree will be the main data structure that a
compiler uses to process the program. By traversing this
tree the compiler can produce machine code.
Secondary function of parser: Syntactic error
detection – report to user where any error in the source
code are.
c

Applications of RE
1. Data Validation:
Test for a pattern within a string.
For example, you can test an input string to see if a
telephone number pattern or a credit card number
pattern occurs within the string. This is called data
validation.
c

Continue…
2. Patten matching:
You can find specific text within a document or input field.
For example, you may need to search an entire Web site,
remove outdated material, and replace some HTML
formatting tags. In this case, you can use a regular
expression to determine if the material or the HTML
formatting tags appears in each file. This process reduces
the affected files list to those that contain material
targeted for removal or change. You can then use a
regular expression to remove the outdated material.
Finally, you can use a regular expression to search for and
replace the tags.
c