Chapter 10 - Rotation• In this chapter we will study the rotational motion of

rigid bodies about a fixed axis. To describe this type of motion we will introduce the following new concepts:

• Angular displacement (symbol: Δθ)• Avg. and instantaneous angular velocity (symbol: ω )• Avg. and instantaneous angular acceleration (symbol: α )• Rotational inertia, also known as moment of inertia

(symbol I )• The kinetic energy of rotation as well as the rotational

inertia;• Torque (symbol τ )• We will have to solve problems related to the above

mentioned concepts.

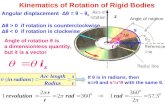
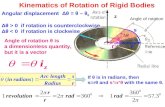
The Rotational Variables• In this chapter we will study the rotational motion of rigid

bodies about fixed axes.• A rigid body is defined as one that can rotate with all its

parts locked together and without any change of its shape.• A fixed axis means that the object rotates about an axis

that does not move, also called the axis of rotation or the rotation axis.

• We can describe the motion of a rigid body rotating about a fixed axis by specifying just one parameter.

• Every point of the body moves in a circle whose center lies on the axis of rotation, and every point moves through the same angle during a particular time interval.

Consider the rigid body of the figure.

We take the z-axis to be the fixed axisof rotation. We define a reference linethat is fixed in the rigid body and isperpendicular to the rotational axis.

The angular position of this line is the angle of the line relative to a fixed direction, which we take as the zero angular position.

In Fig. 11-3 , the angular position is measured relative to the positive direction of the x axis.

rs

From geometry, we know that is given by

(in radians) (10-1)

Here s is the length of arc (arc distance) along a circle and between the x axis (the zero angular position) and the reference line; r is the radius of that circle.

This angle is measured in radians (rad) rather than in revolutions (rev) or degrees. The radian, being the ratio of two lengths, is a pure number and thus has no dimension. Because the circumference of a circle of radius r is 2r, there are 2 radians in a complete circle: rad

rrrev _223601 0

(10-2)

1 rad = 57,30 = 0,159 rev (10-3)

Angular Displacement• If the body of Fig. 10-3 rotates about the

rotation axis as in Fig. 10-4 , changing the angular position of the reference line from 1 to 2, the body undergoes an angular displacement given by:

Δθ = θ2 – θ1 (10-4)• This definition of angular displacement

holds not only for the rigid body as a whole but also for every particle within that body.

• An angular displacement in the counter-clockwise direction is positive, and one in the clockwise direction is negative.

Angular Velocity • Suppose (see Fig. 10-4 ) that our

rotating body is at angular position 1 at time t1 and at angular position 2 at time t2. We define the average angular velocity of the body in the time interval t from t1 to t2 to be

tttavg

12

12 (10-5)

Instantaneous angular velocity, ω:

dtd

tt

0

lim (10-6)

Unit of ω: rad/s or rev/s

Angular Acceleration • If the angular velocity of a rotating body is not

constant, then the body has an angular acceleration, α

• Let 2 and 1 be its angular velocities at times t2 and t1, respectively. The average angular acceleration of the rotating body in the interval from t1 to t2 is defined as:

tttavg

12

12 (10-7)

• Instantaneous angular acceleration, α:

dtd

tt

0

lim (10-8)

Do Sample Problems 10-1 & 10-2, p244-246

Unit: rad/s2 or rev/s2

Consider a point on a rigid body rotating about a fixed axis. At 0 the reference line that connects the origin with point is on the -axis (point ).

Pt

O P x A

Relating the Linear and Angular Variables :

During the time interval , point moves along arc and covers a distance . At the same time, the reference line rotates by an angle .

t P APs

OP

Aθs

O

The arc length and the angle are connected by the equation

where is the distance . The speed of point is , .

sd rds dr OP P v rs r

dt dt dt

Relation between Angular Velocity and Speed :

v rcircumference 2 2 2The period of revolution is given by .

speedr rT Tv r

2T

1Tf

2 f

(10-17)

(10-18)

(10-19) (10-20)

rO

The acceleration of point is a vector that has twocomponents. The first is a "radial" component along the radius and pointing toward point . We have enountered this component in

P

O

The Acceleration :

Chapter 4 where we called it "centripetal" acceleration. Its magnitude is

22

rva rr

The second component is along the tangent to the circular path of and is thus known as the "tangential" component. Its magnitude is

The magnitude of the acceleration vector is

t

P

d rdv da r rdt dt dt

2 2 .t ra a a

ta r

(10-8)

(10-22)

(10-23)

When the angular acceleration is constant we can derive simple expressionsthat give us the angular velocity and the angula

r posi

Rotation with Constant Angular Acceleration :

tion as a function of time. We could derive these equations in the same way we did in Chapter 2. Instead we will simply write the solutions by exploiting the analogy between translational and rotat

Translational Motion Rotational Motion

ional motion using the following correspondence b

etween the two motions.

x

0

2

0

0

2

0

2 20

2 20

(

eq. 1)

(eq. 2)

2

2

2

2

o

o

t

tt

va

v v at

atx x v t

v v a x x

0 (eq. 3)(10-6)

Ori

iv

mi

1 2 3

Consider the rotating rigid body shown in the figure. We divide the body into parts of masses , , ,..., ,....The part (or "element") at has an index and mass .

i

i

m m m mP i m

Kinetic Energy of Rotation :

2 2 21 1 2 2 3 3

The kinetic energy of rotation is the sum of the kinetic 1 1 1energies of the parts: ....2 2 2

K m v m v m v

22

2 2 2 2

1 1 The speed of the th element .2 2

1 1 The term

rotational i

is known as

nertia moment of inerti

2 2

or about the axis of rotation. Tha e axis

i i i i i ii i

i i i ii i

K mv i v r K m r

K m r I I m r

of

rotation be specified because the value of for a rigid body depends on its mass, its shape, as well as on the position of the rotation axis. The rotationalinertia of an object describ

mu

e o

st

s h

I

w the mass is distributed about the rotation axis.2

i ii

I m r212

K I 2 I r dm

(10-31)

(10-32) (10-33)(10-34)

(10-35)

2The rotational inertia . This expression is useful for a rigid body that

has a discreet distribution of mass. For a continuous distribution of mass the s

i ii

I m rCalculating the Rotational Inertia :

2

um

becomes an integral, .I r dm

In the table below we list the rotational inertias for some rigid bodies.2 I r dm

(10-10)

We saw earlier that depends on the position of the rotation axis.For a new axis we must recalculate the integral for . A simpler method takes advantage parallel-axis t of the

II

Parallel - Axis Theorem :

com

Consider the rigid body of mass shown in the figure. We assume that we know the rotational inertia about a rotation axis that passes through the center of mass and is perpen

heorem.

dicular t

MI

O o the page.

The rotational inertia about an axis parallel to the axis through that passesthrough point , a distance from , is given by the equation

I OP h O

2comI I Mh (10-36)

A

com

We take the origin to coincide with the center of mass of the rigid body shownin the figure. We assume that we know the rotational inertia

for an axis that i

O

I

Proof of the Parallel - Axis Theorem :

s perpendicular to the page and passes through . O

We wish to calculate the rotational inertia about a new axis perpendicular to the page and passing through point with coordinates , . Consider

an element of mass at point with coordinates

IP a b

dm A x

2 2

2 22

2 2 2 2

, . The distance

between points and is .

.

2 2 . The second

and third integrals are zero. The first

y r

A P r x a y b

I r dm x a y b dm

I x y dm a xdm b ydm a b dm

Rotational Inertia about :P

2 2 2com

2 2

integral is . The term .

Thus the fourth integral is equal to

I a b h

h dm Mh

2

comI I Mh

Do Sample Problems 10-6 to 10-8, p254-256

In fig. a we show a body that can rotate about an axis through

point under the action of a force applied at point a distance

from . In fig. b we resolve into two com

Tor

ponents, radia

que:

O F P

r O F

l and

tangential. The radial component cannot cause any rotationbecause it acts along a line that passes through . The tangentialcomponent sin on the other hand causes the rotation of the

o

r

t

FO

F F

bject about . The ability of to rotate the body depends on themagnitude and also on the distance between points and .Thus we define as torque The distance is

s

ink n

.now

t

trF rF r

O FF

rF

r P A

as the and it is the

perpendicular distance between point and the vector .The algebraic sign of the torque is assigned as follows:

If a force tends to rotate an objec

moment a

t in the count

rm

O F

F

erclockwise

direction the sign is positive. If a force tends to rotate an object in the clockwise direction the sign is negative.

F

r F (10-13)

(10-39)

(10-41)(10-40)

Draaimoment

For translational motion, Newton's second law connects the force acting on a particle with the resulting acceleration.There is a similar relationship between the torqu

Newton's Second Law for Rotation :

e of a forceapplied on a rigid object and the resulting angular acceleration.

This equation is known as Newton's second law for rotation. We will explore this law by studying a simple body that consists of a point mass at the end

of a massless rod of length . A force is

m

r F

applied on the particle and rotates

the system about an axis at the origin. As we did earlier, we resolve into a tangential and a radial component. The tangential component is responsible for the

F

2

rotation. We first apply Newton's second law for . (eq. 1)The torque acting on the particle is (eq. 2). We eliminate

between equations 1 and 2: .

t t t

t t

t

F F maF r F

ma r m r r mr I

(compare with: )F ma I (10-45)

We have derived Newton's second law for rotation for a special case: a rigid body that consists of a pointmass at the end of a massless rod of length . We willnow

m r

Newton's Second Law for Rotation :

derive the same equation for a general case. O

12

3

i

ri

net

Consider the rod-like object shown in the figure, which can rotate about an axisthrough point under the action of a net torque . We divide the body into parts or "elements" and label them. The

O

1 2 3

1 2 3

1 1 2 2

3 3

elements have masses , , ,..., and they are located at distances , , ,..., from . We apply Newton's secondlaw for rotation to each element: (eq. 1), (eq. 2),

(eq

n

n

m m m mr r r r O

I II

21 2 3 1 2 3

1 2 3 net

. 3), etc. If we add all these equations we get

... ... . Here is the rotational inertia

of the th element. The sum ... is the net torque applied.T

n n i i i

n

I I I I I m r

i

1 2 3he sum ... is the rotational inertia of the body. Thus we end up with the equation

nI I I I I

net I (10-15)(10-42)

Rotational Motion Translational Motion

xv

Analogies Between Translational and Rotational Motion

0 0

2

0 0

2

2

0

2 20

20 0

2

2

2

2

o

o

av v at

atx x v t

v v a x x

t

tt

2 2

2

2

mvK

mF ma

FP Fv

IK

II

P (10-18)