Accelerated Motion Velocity, acceleration and gravity.

Accelerated MotionAccelerated MotionVelocity, acceleration and gravityVelocity, acceleration and gravity

How fast do things fallHow fast do things fall

ReflexesReflexes

Position-Time GraphsPosition-Time Graphs

11 22 33 44

Velocity v. TimeVelocity v. Time

DefinitionsDefinitions VelocityVelocity

Change in Change in position with position with respect to timerespect to time

v = v = ΔΔd/d/ΔΔt t Which can be written as:Which can be written as:

(d(dfinalfinal-d-dinitialinitial)/(t)/(tfinalfinal-t-tinitialinitial))

Common notation:Common notation:

(d(dff––ddii)/(t)/(tff–t–tii))

AccelerationAcceleration Change in Change in

velocity with velocity with respect to timerespect to time

a = a = ΔΔv/v/ΔΔt t Which can be written as:Which can be written as:

(v(vfinalfinal-v-vinitialinitial)/(t)/(tfinalfinal-t-tinitialinitial))

Common notation :Common notation :

(v(vff–v–vii)/(t)/(tff–t–tii))

Velocity to AccelerationVelocity to Acceleration

v=v=ΔΔd/d/ΔΔt=(dt=(dfinalfinal–d–dinitialinitial)/(t)/(tfinalfinal–t–tinitialinitial))

a=a=ΔΔv/v/ΔΔt=(vt=(vfinalfinal–v–vinitialinitial)/(t)/(tfinalfinal–t–tinitialinitial))

Average AccelerationAverage Acceleration a =a =ΔΔv/v/ΔΔt=(vt=(vfinalfinal–v–vinitialinitial)/(t)/(tfinalfinal–t–tinitialinitial))

ff = final= final ii = initial = initial

If tIf tinitial initial = 0= 0 a = (va = (vfinalfinal – v – vinitialinitial)/t)/tfinalfinal

Or:Or: vvff = v = vii +at +atff

Positive and Negative Positive and Negative Acceleration Acceleration

Practice ProblemPractice Problem A soccer player is running at a A soccer player is running at a

constant velocity of 50.0km/h constant velocity of 50.0km/h (31mph). The player falls and (31mph). The player falls and skids to a halt in 4.0 seconds.skids to a halt in 4.0 seconds. What is the average acceleration of What is the average acceleration of

the player during the skid?the player during the skid? What is the plot of the velocity vs. What is the plot of the velocity vs.

time?time?

Practice ProblemPractice Problem

A water balloon in the sling of a A water balloon in the sling of a water balloon launcher undergoes water balloon launcher undergoes a constant acceleration 25m/s^2 a constant acceleration 25m/s^2 for 1.5s.for 1.5s. What is the velocity of the water What is the velocity of the water

balloon right after launch?balloon right after launch?


A car accelerates from rest at 5 m/s2 for A car accelerates from rest at 5 m/s2 for 5 seconds. It moves with a constant 5 seconds. It moves with a constant velocity for some time, and then velocity for some time, and then decelerates at 5 m/s2 to come to rest. decelerates at 5 m/s2 to come to rest. The entire journey takes 25 seconds. The entire journey takes 25 seconds. Plot the velocity-time graph of the Plot the velocity-time graph of the motion.motion.


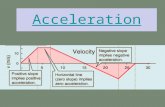
Determine the Determine the accelerations for accelerations for aa11, a, a22, a, a33, and a, and a44 for each time for each time interval. interval.

aa11= 4/5= 4/5

aa22= (4-4)/(10-5)= (4-4)/(10-5)

aa33= (16-4)/(20-10)= (16-4)/(20-10)

aa44= (0-16)/(30-20)= (0-16)/(30-20)

Frictionless CarsFrictionless Cars

HypotenuseHypotenuseGravityGravity

Frictionless Car PlotsFrictionless Car Plots

Good Reading on PlotGood Reading on Plot

Velocity with Constant Velocity with Constant AccelerationAcceleration

Given:Given:

Solve Solve for tfor tff::

Substitute in: Substitute in:

Yeilds:Yeilds:

2½

½

2


Solve for Solve for vfvf ½

2

½

2

1 12

2

21 12

2

2

22

2 2 22 2

222

GraphsGraphs Determine which equations provide the Determine which equations provide the

area under the graph. (let ti = 0)area under the graph. (let ti = 0)

½ ½ (v(vff-v-vii))

ttff½ ½ aa

(t(tff-t-tii))

22

(v(vff-v-vii))(t(tff-t-tii))

22

(t(tff-t-tii))1122

Vel

ocity

(m

/s)

Vel

ocity

(m

/s)

Time (s)Time (s)

1)1)

2)2)

3)3)


Equation to remember:Equation to remember: vvff^2 = v^2 = vii^2 +2a(d^2 +2a(dff-d-dii))

Position with Average Position with Average AccelerationAcceleration

ΔΔd/d/ΔΔt = t = ΔΔv + ½ a v + ½ a ΔΔtt ΔΔd = d = ΔΔvvΔΔt + ½ a t + ½ a ΔΔt^2t^2

When tWhen tii = 0: = 0: ddff - d - dii = v = viittff + ½ at + ½ atff^2^2


Equation to remember:Equation to remember: Final position = initial position + (change in velocity)*time + ½ Final position = initial position + (change in velocity)*time + ½

(acceleration)*(time squared)(acceleration)*(time squared)

ddff = d = dii + (v + (vff-v-vii)t + ½ at^2 )t + ½ at^2

Table 3-3 Page 68Table 3-3 Page 68 Equations of Motion for Uniform Equations of Motion for Uniform

AccelerationAcceleration

EquationEquation VariableVariabless

Initial Initial ConditiConditionsons

Average AccelerationAverage Acceleration ttff,v,vff,a,a vvii


ttff,d,dff,a,a ddii,v,vii


ddff,v,vff,a,a ddii,v,vii

Free Fall on the Moon Free Fall on the Moon

Group Project pg 78Group Project pg 78 How fast is the How fast is the

Earth spinning?Earth spinning? 0.5 km/sec 0.5 km/sec

How fast is the How fast is the Earth revolving Earth revolving around the Sun?around the Sun? 30 km/sec 30 km/sec

How fast is the Solar How fast is the Solar System moving System moving around the Milky around the Milky Way Galaxy?Way Galaxy? 250 km/sec 250 km/sec

How fast is our Milky How fast is our Milky Way Galaxy moving Way Galaxy moving in the Local Group of in the Local Group of galaxies?galaxies? 370 km/sec370 km/sec

2

21

os

tt

vc

2

21

os

tt

vc

Free FallFree Fall

All Objects fall at All Objects fall at the same speed the same speed regardless of regardless of mass (if you can mass (if you can neglect wind neglect wind resistance).resistance).

Free FallFree Fall

A ball or a A ball or a bullet?bullet?

..

..

21

2f i id d v t at

21

2iy v t gt

Position with Average AccelerationPosition with Average Acceleration

Height with constant gravityHeight with constant gravity

FallingFalling21

2iy v t gt

Poor little guyPoor little guy21

2iy v t gt

GraphsGraphs

Cart MovementCart Movement

Practice ProblemsPractice Problems

If you throw a ball straight upward, it If you throw a ball straight upward, it will rise into the air and then fall will rise into the air and then fall back down toward the ground.back down toward the ground.

Imagine that you throw the ball with Imagine that you throw the ball with an initial velocity of 10.0 m/s.an initial velocity of 10.0 m/s. a. How long does it take the ball to reach a. How long does it take the ball to reach

the top of its motion?the top of its motion? b. How far will the ball rise before it b. How far will the ball rise before it

begins to fall?begins to fall? c. What is its average velocity during c. What is its average velocity during

this period?this period?

a. How long does it take the ball to reach the a. How long does it take the ball to reach the top of its motion?top of its motion?

2

0.00 10.0 /1.02

9.80 /

f i

f if

v v at

v v m st s

a m s

b. How far will the ball rise before it begins to b. How far will the ball rise before it begins to fall?fall?

1

21

(10.0 / 0.00 / )(1.02 )2

5.1

f id v v t

m s m s s

m

c. What is its average velocity during this c. What is its average velocity during this period?period?

5.1 0.0

1.025 /

f id dv

tm m

sm s


A sudden gust of wind increases A sudden gust of wind increases the velocity of a sailboat relative the velocity of a sailboat relative to the water surface from 3.0 to the water surface from 3.0 m/s to 5.5 m/s over a period of m/s to 5.5 m/s over a period of 60.0 s.60.0 s. a. What is the average a. What is the average

acceleration of the sailboat?acceleration of the sailboat? b. How far does the sailboat travel b. How far does the sailboat travel

during the period of acceleration?during the period of acceleration?

a. What is the average acceleration of the a. What is the average acceleration of the sailboat?sailboat?

2

5.5 / 3.0 /

60.0

0.042 /

f iv vva

t tm s m s

s

m s

b. How far does the sailboat travel during the b. How far does the sailboat travel during the period of acceleration?period of acceleration?

2

22

1

21

0.0 (3.0 / )(60.0 ) 0.042 / 60.02

0.0 180 75.6 255

f i id d v t at

m m s s m s s

m m m m


A car starts from rest with an acceleration A car starts from rest with an acceleration of 4.82 m/s^2 at the instant when a of 4.82 m/s^2 at the instant when a second car moving with a velocity of 44.7 second car moving with a velocity of 44.7 m/s (100mph by the way) passes it in a m/s (100mph by the way) passes it in a parallel line. How far does the first car parallel line. How far does the first car move before it overtakes the second car?move before it overtakes the second car? Setup an equation or graphSetup an equation or graph

Setup the equation Setup the equation

2 21 1 1 2 2 2

1 1

2 2car car car car car card v t a t d v t a t

00 00

21 2

1

2 car cara t v t

PositionPositiondd

VelocityVelocityv=v=ΔΔd/d/ΔΔtt

AccelerationAccelerationa=a=ΔΔv/v/ΔΔt t

Accelerated Motion Velocity, acceleration and gravity.

Documents

Transcript of Accelerated Motion Velocity, acceleration and gravity.