1 Bargaining Markets u Two populations: Buyers and Sellers u A sellers has 1 indivisible unit to...
-
Upload
carol-norman -
Category
Documents
-
view
219 -
download
0
description
Transcript of 1 Bargaining Markets u Two populations: Buyers and Sellers u A sellers has 1 indivisible unit to...

1
Bargaining & Markets
Two populations: Buyers and Sellers A sellers has 1 indivisible unit to sell A Buyer has 1 unit of divisible money If they agree on a price at period t, their
utilities are: δtp, δt(1-p). Random matching of pairs (buyer &
seller) Bargaining breaks down after 1 period,
if there was no agreement

2
Bargaining & Markets
The Populations: Continuous or finite sets B, S
Bargaining: Nash Bargaining Solution, with the expected continuation values δVS , δVB as the disagreement point.
A pair that reached agreement leaves the market
Matching: If B > S then all sellers are matched and a buyer is matched with probability S/B.

3
Bargaining & Markets
Model 1: The populations sizes B, S do not change with time. i.e. new individuals enter the market to replace those that left.
( Assume B > S )
We seek an equilibrium in stationary and anonymous strategies

4
Bargaining & MarketsModel 1:Model 1: B, S constantB, S constant
B S B S
S B
S1 - δV
if δV ++ δV 1 - δV
δV < 1 then :- δVp* = = + δV
2 2

5
Bargaining & MarketsModel 1:Model 1: B, S constantB, S constant
B
B
B
S B
S BB
S
S S(1 - p*)+ (1 - )δVB B
VδV
if δV + δV < 1
=if δV
1 - δV
+ δ
+
V 1
p*
>
δV=2

6
Bargaining & MarketsModel 1:Model 1: B, S constantB, S constant
S B
S
S
B
B
S
S
if δV + δV < 1=
if δV +
p*V
δV
1 - δV
δV
+p
>
δV* =
1
2

7
Bargaining & MarketsModel 1:Model 1: B, S constantB, S constant
B
B
B
S
S
S
B
S B
S B
B
S B
S
if δV + δV < 1
=if δV + δV > 1
if δV + δV < 1=
if δ
S S(1 - p*)+ (1 - )δVB B
VδV
p*V
δV
1 - δV
V + δ
+
V > 1
δVp* =2

8
Bargaining & MarketsModel 1:Model 1: B, S constantB, S constant
B
B
B
S
S
S
B
S B
S B
B
S B
S
if δV + δV < 1
=if δV + δV > 1
if δV + δV < 1=
if δ
S S(1 - p*)+ (1 - )δVB B
VδV
p*V
δV
1 - δV
V + δ
+
V > 1
δVp* =
2
0,0similarly
an
if then
d
B B
B
S B
S
S B
δV + δV > 1
δV + δV
V = δVV
V< 1.

9
Bargaining & MarketsModel 1:Model 1: B, S constantB, S constant
S B
B B
S
B S
S SV = (1 - p*)+ (1 - )δVB B
V = p*1 - δV + δVp* =
2δV + δV < 1

10
Bargaining & MarketsModel 1:Model 1: B, S constantB, S constant
S B
B B
S
B S
S SV = (1 - p*)+ (1 - )δVB B
V = p*1 - δV + δV
p* =2
δV + δV < 1
1p* = S2 - δ + δB

11
Bargaining & MarketsModel 1:Model 1: B, S constantB, S constant
1p* =S2 - δ + δB
121
Bas δ , p*B + S
21B > S , p* >
12 .as S , p*
12 .as δ 0, p*
Find p when S >B !!!!

12
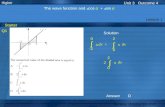
Bargaining & MarketsModel 1:Model 1: B, S constantB, S constant
q
p
S
1
B
Supply
Demand
Microeconomics I ??
p = 1p = 11p* =
S2 - δ + δB
121
Bas δ , p*B + S

13
Bargaining & Markets
Model 2: No new individuals enter the market. The populations shrink over time.
Let the initial populations be of sizes B0 , S0. Since equal numbers of buyers & sellers leave the market, the populations B,S at any period satisfy: B -S = B0 - S0.
( Assume B0 > S0 )

14
Bargaining & MarketsModel 2: No new entryModel 2: No new entry
If there is agreement then all pairs leave and only B0 - S0 buyers remain.
If there is agreement and one pair deviates then there will remain B0 - S0 +1 buyers and 1 seller in the market
The disagreement point for all pairs is:
B 0 0 S 0 0δV 1,B - S + 1 , δV 1,B - S + 1

15
Bargaining & MarketsModel 2: No new entryModel 2: No new entry
B S1 - δV 1,B - S + 1 + δV 1,B - S + 1p* (S,B) =
2
SV S,B p* (S,B)
BSV S,B = 1 - p* (S,B)B
set S = 1
B S1 - δV 1,B + δV 1,Bp* (1,B) =
2
SV 1,B p* (1,B)
B1V 1,B = 1 - p* (1,B)B

16
Bargaining & MarketsModel 2: No new entryModel 2: No new entry
SV 1,B p* (1,B)
B1V 1,B = 1 - p* (1,B)B
B S1 - δV 1,B + δV 1,Bp* (1,B) =
2
11 - δBp* (1,B) = 12 - - δ
B

17
Bargaining & MarketsModel 2: No new entryModel 2: No new entry
B S1 - δV 1,B - S + 1 + δV 1,B - S + 1p* (S,B) =
211 - δBp* (1,B) = 12 - δ - δ
B
δB-S+1
δB-S+1
1 -p* (1,B - S + 1) =
2 - δ - S= V (1,B - S + 1)
1B B-S+1V (1,B - S + 1) = (1 - p* (1,B - S + 1))

18
Bargaining & MarketsModel 2: No new entryModel 2: No new entry
δB-S+1
δB-S+1
1 -p* (S,B) =
2 - δ -
S < B, δ 1, p* (S,B) 1
12S = B p* (S,B) =
12S < B p* (S,B) >

19
Bargaining & MarketsModel 2: No new entryModel 2: No new entry
δB-S+1
δB-S+1
1 -p* (S,B) =
2 - δ -
lim
1δ 12
1 if S < Bp* (S,B) =
if S = B
Find p* when S >B !!!!

20
Bargaining & Markets
Justifying the assumptions of Models 1 & 2
The MarketModel 1 or 2
Individuals borneach period
B > Sε - cost of entry
B* > S *

21
Bargaining & Markets
Model 1 (constant populations)
Equal numbers of buyers & sellers should enter each period
The MarketModel 1
Individuals borneach period
B > Sε - cost of entry
B* > S *
Bif V (S*,B*) > ε then all B will enter,
and there is not enough S to keep nos. equal
B V (S*,B*) = ε

22
Bargaining & Markets
B > S ε - cost of entry B* > S *
B V (S*,B*) = ε
Justifying Model 1Justifying Model 1
Could S* > B* ??
1
B 2B*S*
1ε = V (S*,B*) = >2 - +
12if ε < then S* < B*

23
Bargaining & Markets
B > S ε - cost of entry B* > S *
B V (S*,B*) = ε
Justifying Model 1Justifying Model 1
S* < B*
S*B*
B S*B*
V (S*,B*) = = ε2 - +
S S*
B*
1 1 -p* = V (S*,B*) = = > ε2 - + 2 -
2 - δ εS * =B* 1 - δε
S* = S

24
Bargaining & Markets
B > S ε - cost of entry B* > S *
B V (S*,B*) = ε
Justifying Model 1Justifying Model 1
S* < B* 2 - δ εS * =
B* 1 - δεS* = S
1 - δεB* = S2 - δ ε
is B* < B ??
S ,S enter each period
S*,B* 0,B* S * S*,S *

25
Bargaining & Markets
B > S ε - cost of entry B* > S *
B V (S*,B*) = ε
Justifying Model 1Justifying Model 1
S* < B* 2 - δ εS * =
B* 1 - δε
1 -p* =2 -
S ,S S*, S *
0, S * 1as 0 : p*B* 2 - δ
as 0 , δ 0 : p* 1

26
Bargaining & Markets
B > S ε - cost of entry B* > S *
Justifying Model 2Justifying Model 2
δB-S+1
δB-S+1
1 -p* (S,B) =
2 - δ -
assume δ 1
lim
1δ 12
1 if S < Bp* (S,B) =
if S = B
Entry has a large effect on prices
Assume that an entrant anticipates his
effect on prices
?

27
Bargaining & Markets
B > S ε - cost of entry B* > S *
Justifying Model 2Justifying Model 2
if S* < B* then p* ~ 1 and B's will not enter
lim
1δ 12
1 if S < Bp* (S,B) =
if S = BAssume that an
entrant anticipates his effect on prices
?
12if S* > B* then p* <
and B's will enter until S* = B*

28
Bargaining & Markets
B > S ε - cost of entry B* > S *
Justifying Model 2Justifying Model 2
Let B* = S* = E12p* =
if another B enters price will be2 - δ p* = ~ 1
4 - 3δ δB-S+1
δB-S+1
1 -p* (S,B) =
2 - δ -
B* = S *
and his gain will be less than ε i.e. he w notill enter
Topics -5